第二部へようこそ 基本に戻る シリーズ。 の中に 最初の部分では、線形回帰とコスト関数を使用して、住宅価格データに最適な線を見つける方法について説明しました。 ただし、複数のテストを行うこともわかりました インターセプト 値は退屈で非効率的です。 この第 XNUMX 部では、勾配降下法について深く掘り下げます。これは、完璧なものを見つけるのに役立つ強力な手法です。 インターセプト モデルを最適化します。 その背後にある数学を調べて、線形回帰の問題にどのように適用できるかを見ていきます。

勾配降下法は強力な最適化アルゴリズムです。 曲線の最小点を迅速かつ効率的に見つけることを目的としています。 このプロセスを視覚化する最良の方法は、あなたが丘の頂上に立っていると想像することです.金で満たされた宝箱が谷であなたを待っていると想像してください.

ただし、外は真っ暗で何も見えないため、谷の正確な位置は不明です。 さらに、他の誰よりも先に谷に到達したいと考えています (すべての宝物を自分のものにしたいからです)。 勾配降下は、地形をナビゲートしてこれに到達するのに役立ちます 最適な ポイント 効率的かつ迅速に. 各ポイントで、何歩進むべきか、どの方向に進む必要があるかを教えてくれます。

同様に、勾配降下法は、アルゴリズムによってレイアウトされたステップを使用して線形回帰問題に適用できます。 最小値を見つけるプロセスを視覚化するために、 MSE 曲線。 曲線の方程式は次のとおりであることは既にわかっています。

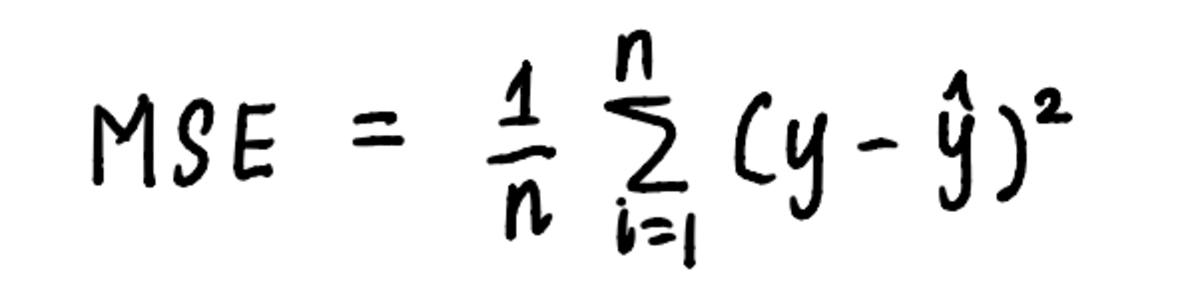
曲線の方程式は、MSE の計算に使用される方程式です。

そしてから 前の記事、私たちは次の式を知っています MSE 私たちの問題は次のとおりです。

ズームアウトすると、 MSE 曲線 (これは私たちの谷に似ています) は、一連の インターセプト 上記の式の値。 それでは 10,000 個の値をプラグインして インターセプト、次のような曲線を取得します。

実際には、MSE 曲線がどのように見えるかはわかりません。

目標はこれの底に到達することです MSE これは、次の手順に従って実行できます。

ステップ 1: 切片値のランダムな初期推定から開始する

この場合、 インターセプト 値は0です。

ステップ 2: この時点での MSE 曲線の勾配を計算する

　 勾配 ある点での曲線の曲線は、その点での接線 (線がその点でのみ曲線に接するという派手な言い方) で表されます。 たとえば、ポイント A では、 勾配   MSE 曲線は、切片が 0 に等しい場合、赤い接線で表すことができます。

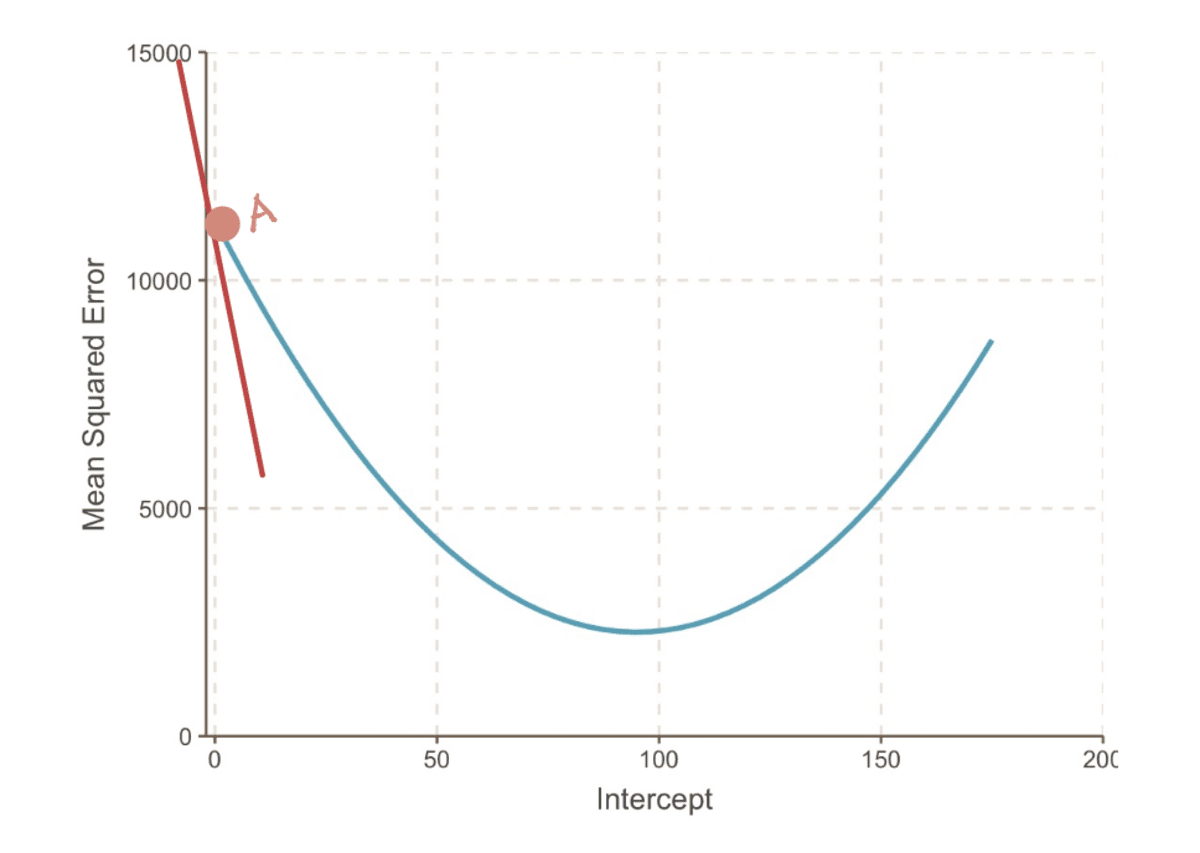
切片 = 0 の場合の MSE 曲線の勾配

の値を決定するために、 勾配、微積分の知識を適用します。 具体的には、 勾配 に関する曲線の導関数に等しい インターセプト 特定の時点で。 これは次のように表されます。

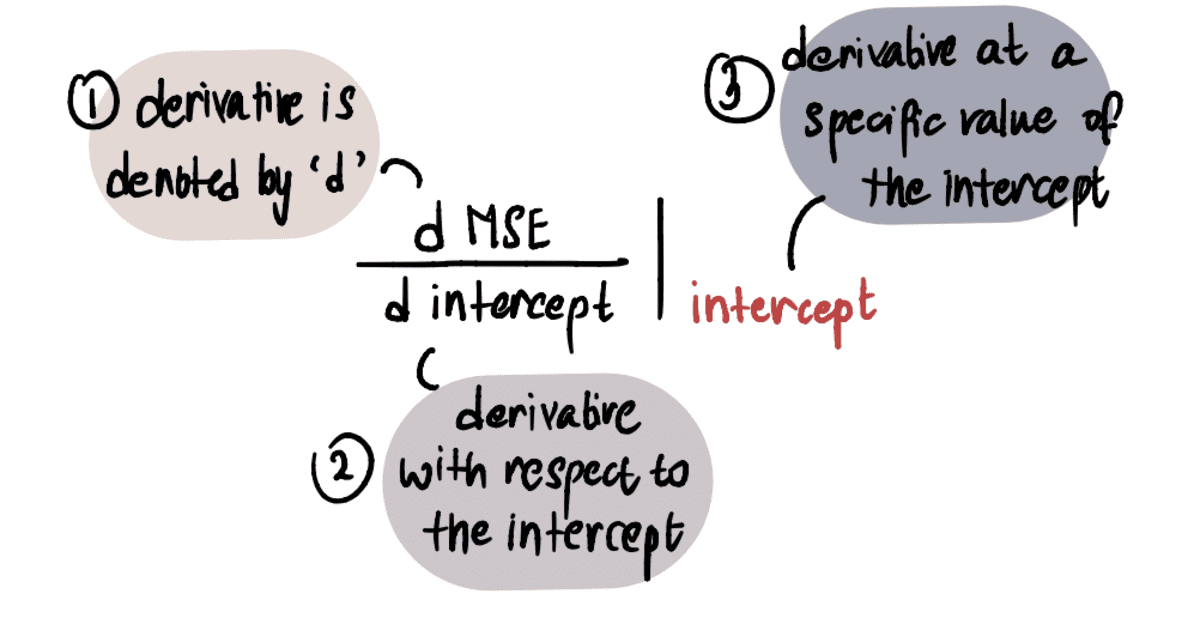
注：デリバティブに慣れていない場合は、これを見ることをお勧めします カーン アカデミーのビデオ 興味があれば。 それ以外の場合は、次の部分をざっと見ても、記事の残りの部分をたどることができます。

計算します MSE 曲線の導関数 次のように：

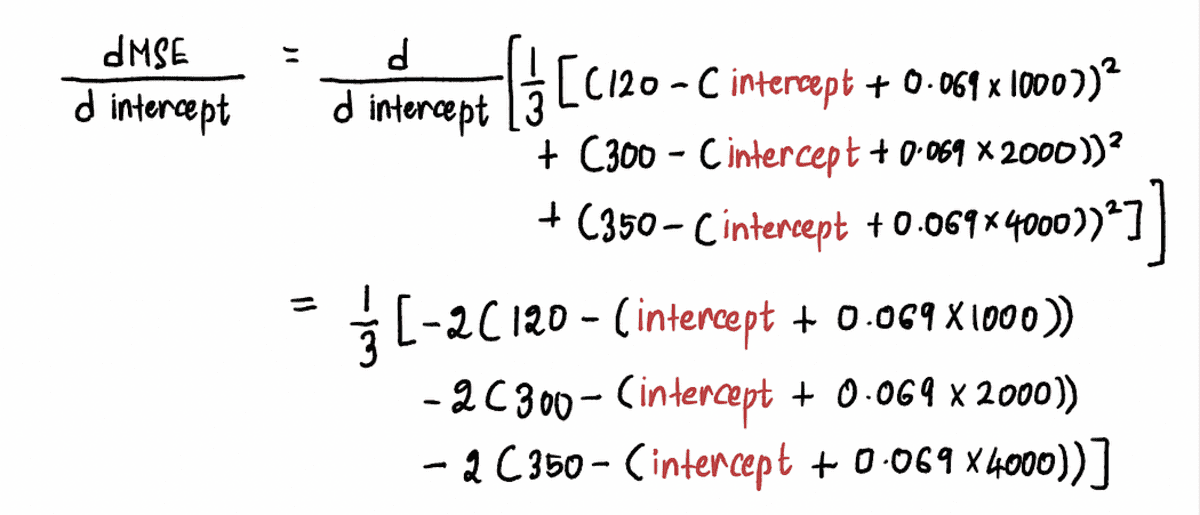
今すぐ見つけるために 点 A での勾配の値を代入します。 インターセプト 上記の式の点Aで。 以来 インターセプト = 0、点 A での導関数は次のとおりです。

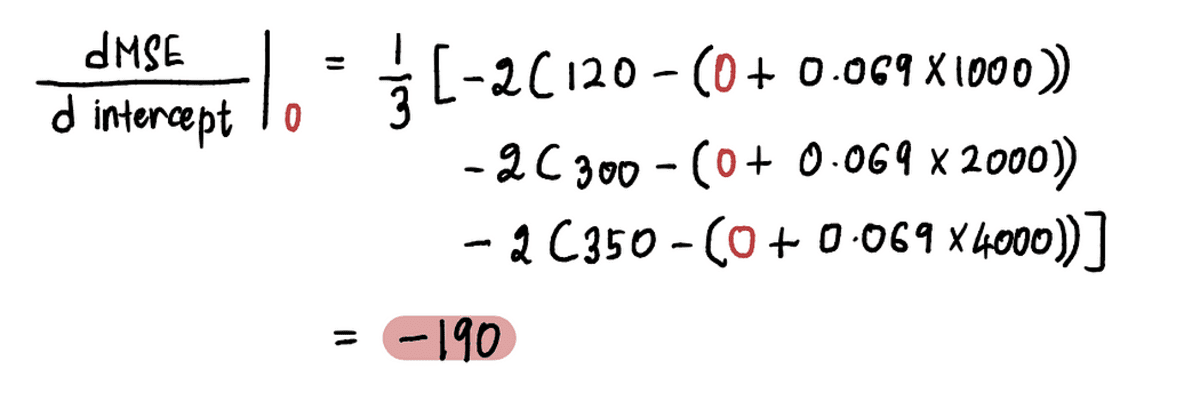
だから、 インターセプト = 0、 勾配 = -190

注意： 最適値に近づくと、勾配値はゼロに近づきます。 最適値では、勾配はゼロに等しくなります。 逆に、最適値から離れるほど、勾配は大きくなります。

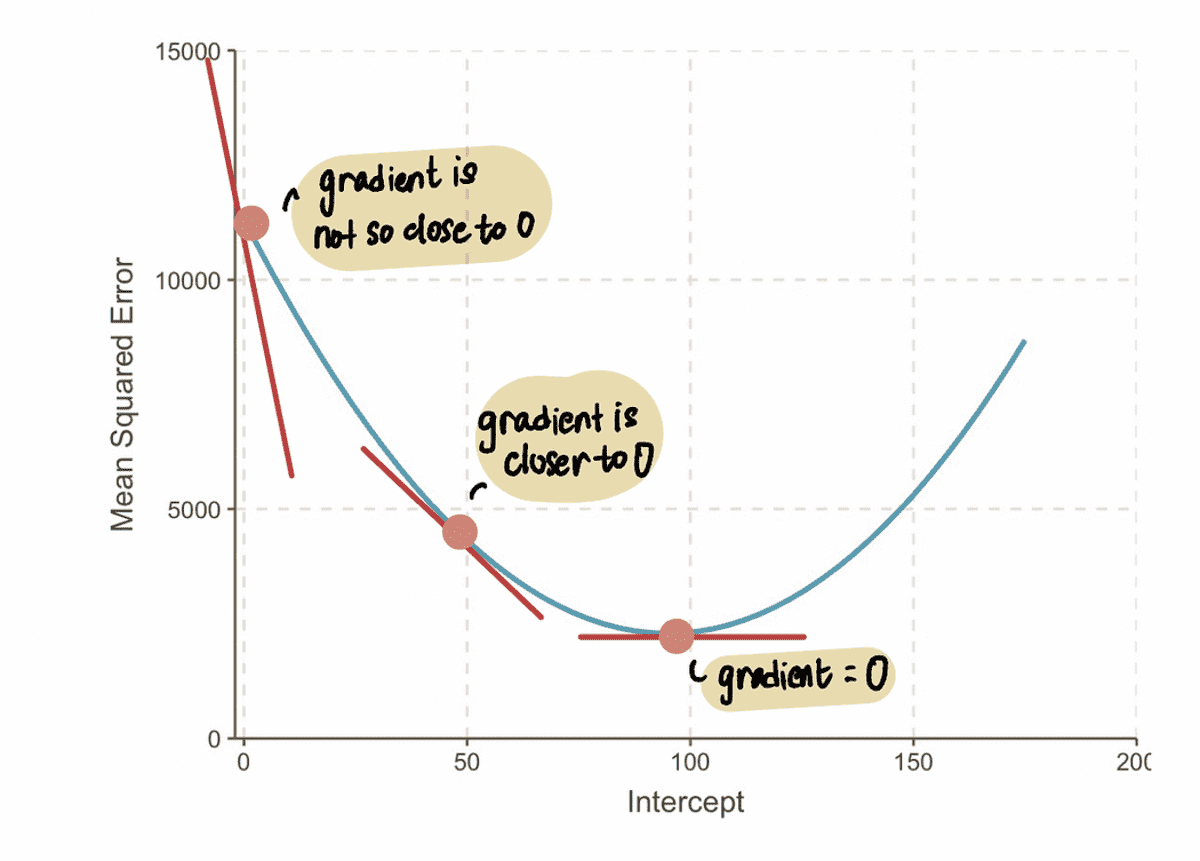
このことから、ステップ サイズは 勾配、それは私たちが赤ちゃんの一歩を踏み出すか、大きな一歩を踏み出すかを教えてくれるからです. これは、 勾配 曲線の が 0 に近い場合は、最適値に近づいているため、段階を踏む必要があります。 そしてもし 勾配 が大きいほど、より速く最適値に到達するには、より大きなステップを踏む必要があります。

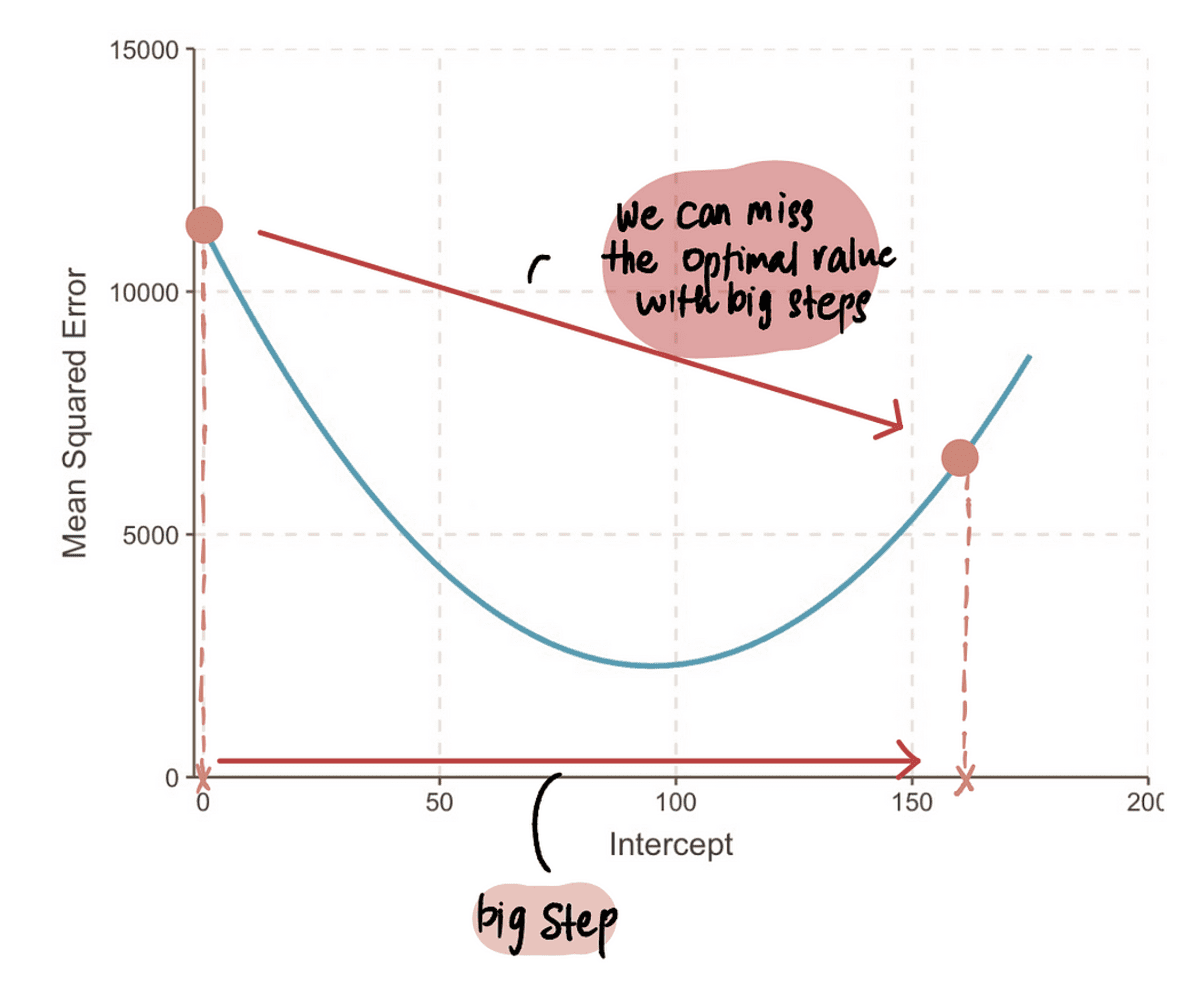
注意： しかし、非常に大きな一歩を踏み出すと、大きなジャンプをして最適なポイントを逃す可能性があります。 ですから、注意が必要です。

ステップ 3: 勾配と学習率を使用してステップ サイズを計算し、切片値を更新する

私たちはそれを見るので、 刻み幅 および 勾配 は互いに比例し、 刻み幅 を乗じて決定されます。 勾配 と呼ばれる事前定義された定数値によって 学習率:

　 学習率 の大きさを制御します 刻み幅 実行されるステップが大きすぎたり小さすぎたりしないようにします。

実際には、学習率は通常、小さい正の数です。 0.001。 しかし、私たちの問題では、それを 0.1 に設定しましょう。

したがって、切片が 0 の場合、 ステップ サイズ = 勾配 x 学習率 = -190*0.1 = -19。

に基づく 刻み幅 上で計算し、更新します インターセプト （別名、現在の場所を変更します） これらの同等の式のいずれかを使用します。

新しいものを見つけるために インターセプト このステップでは、関連する値をプラグインします…

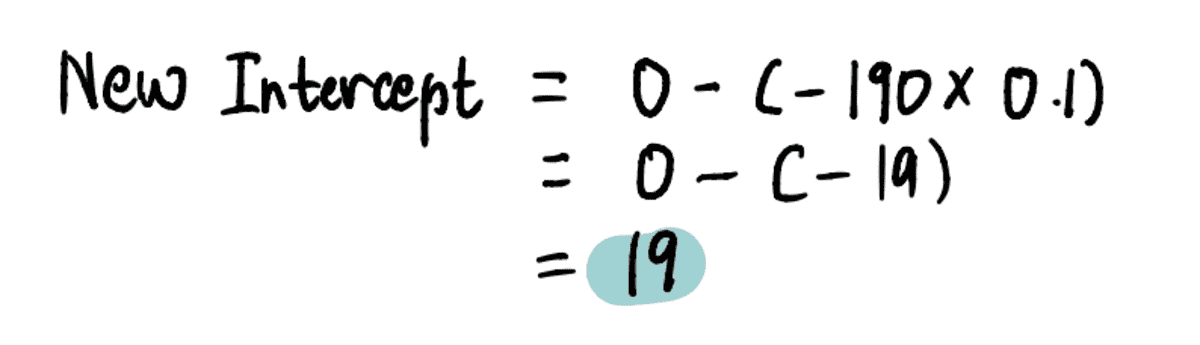
…そして、新しい インターセプト = 19。

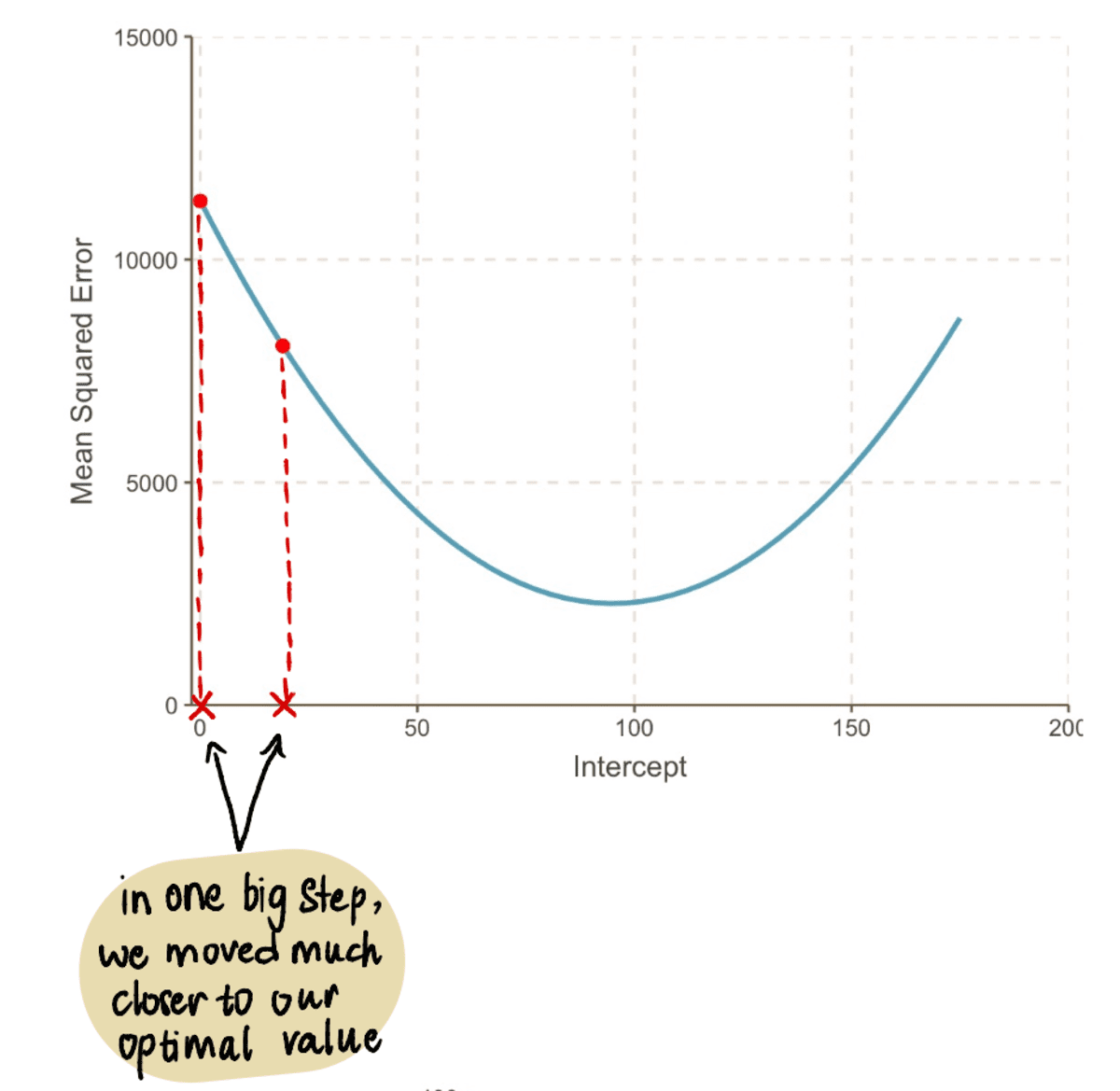
この値を MSE 式から、 MSE 時 インターセプト 19 = 8064.095 です。 XNUMX つの大きなステップで、最適な値に近づき、 MSE.

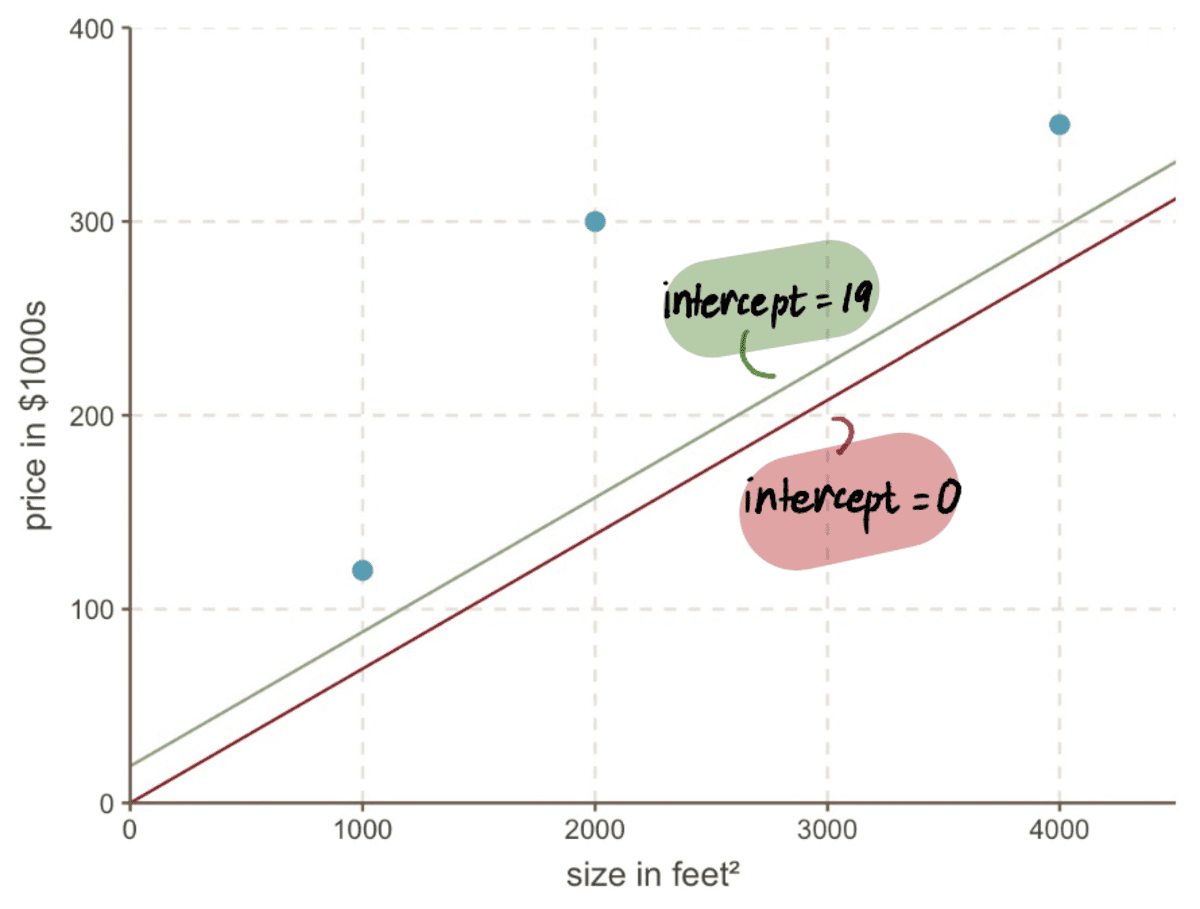
グラフを見ても、新しい行がどれだけ優れているかがわかります インターセプト 19 は、古い線よりもデータに適合しています。 インターセプト 0:

ステップ 4: ステップ 2 ～ 3 を繰り返す

更新された インターセプト の値です。

たとえば、新しい インターセプト この繰り返しの値は 19 です。 ステップ 2、この新しいポイントで勾配を計算します。

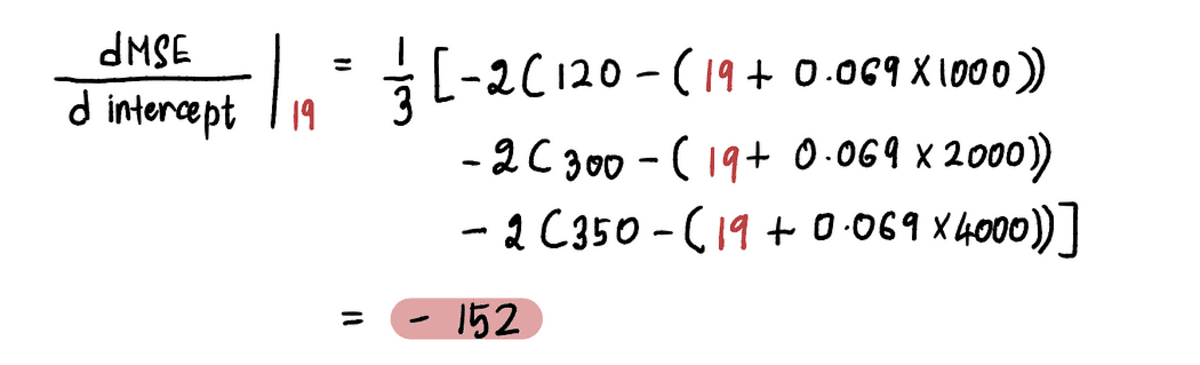
そして、 勾配   MSE 切片値 19 での曲線は -152 です (下の図の赤い接線で表されています)。

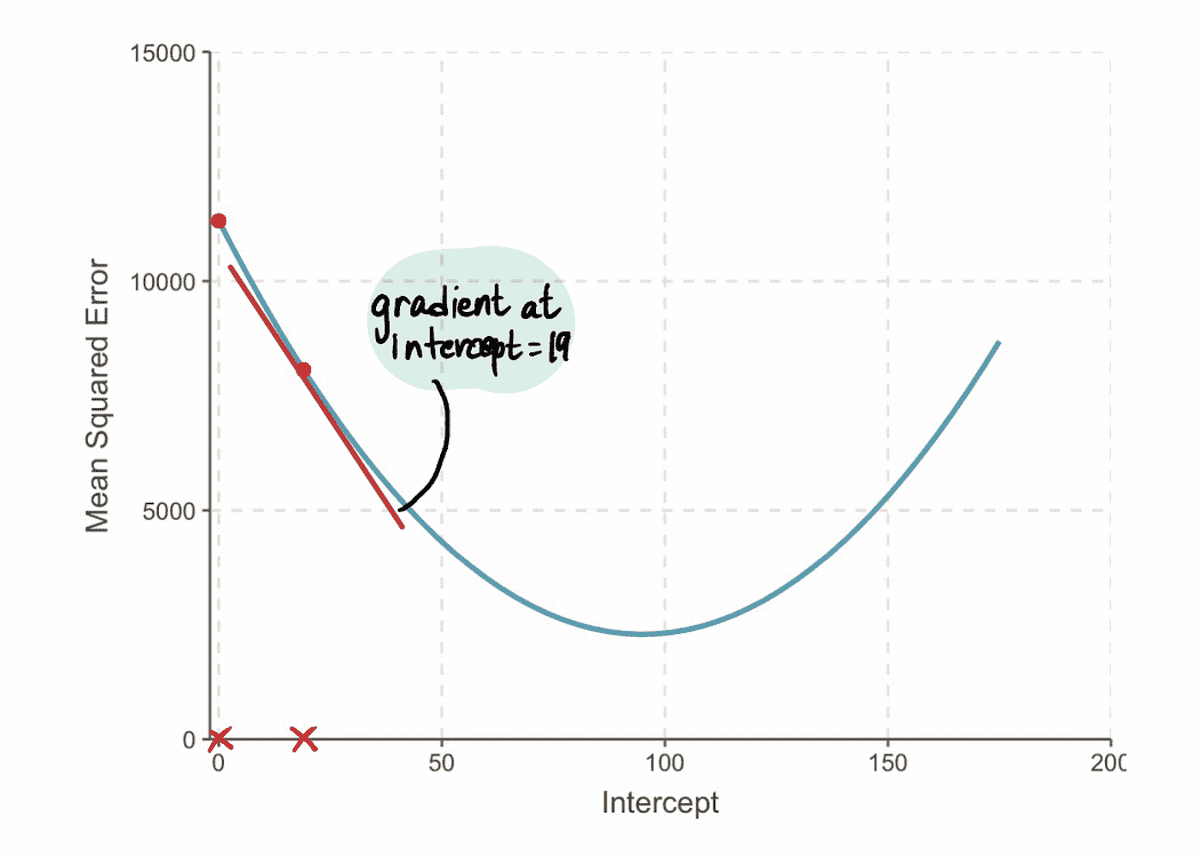
次に、それに合わせて ステップ 3、計算してみましょう 刻み幅:

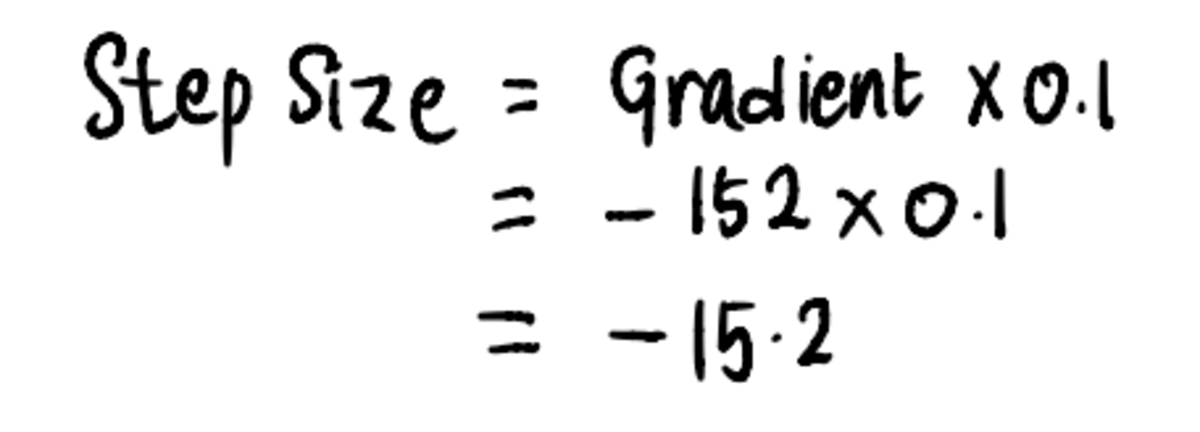
その後、更新します インターセプト 値：

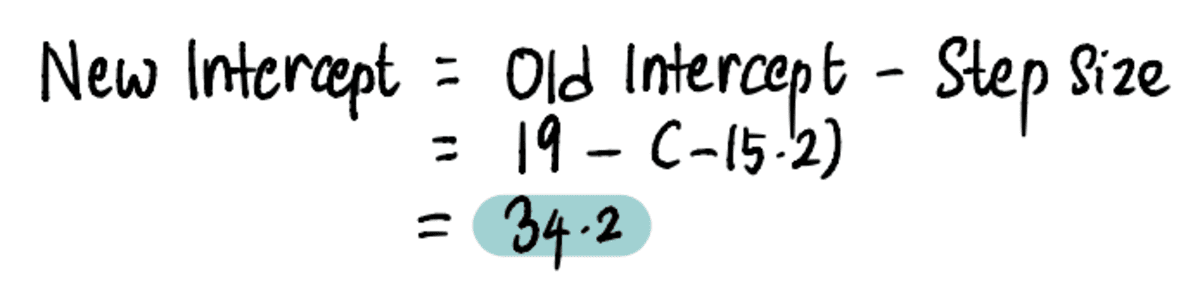
これで、行を前の行と比較できます インターセプト 新しいインターセプト19…の新しいラインへの34.2の

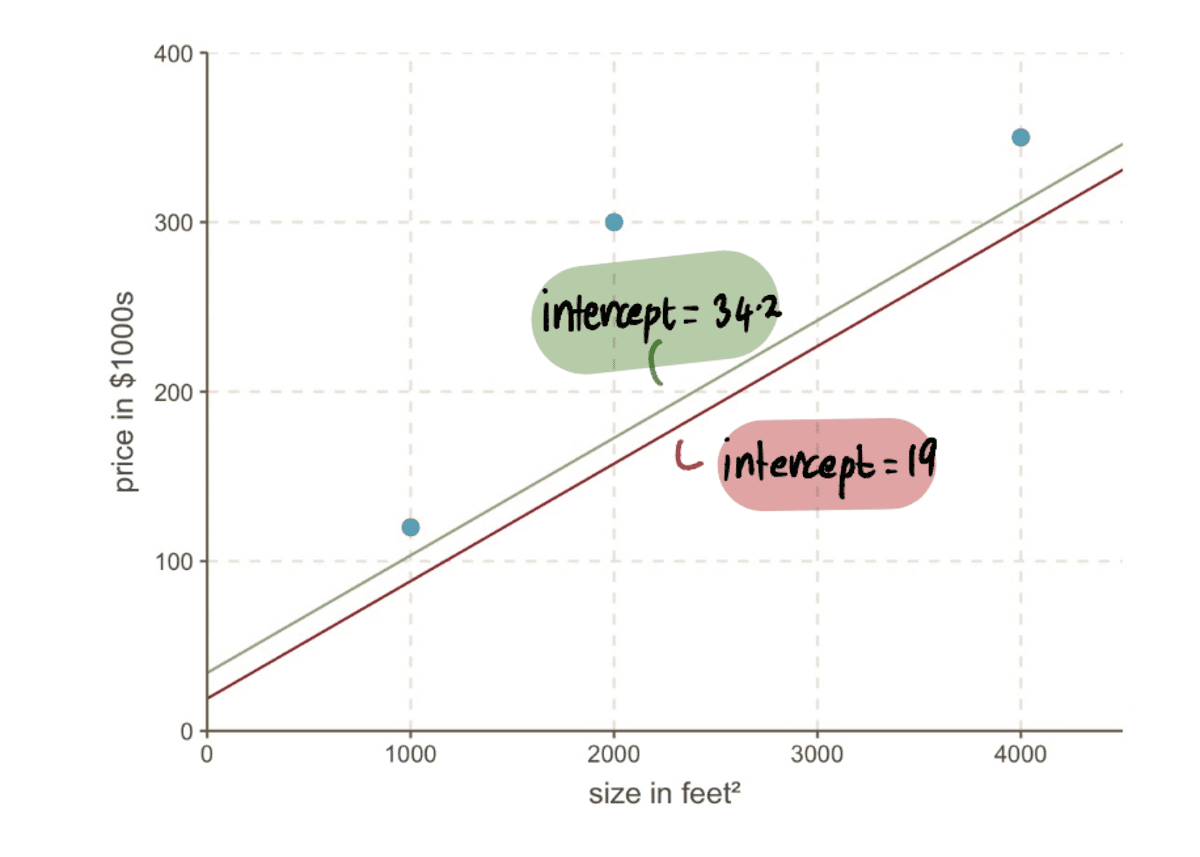
…そして、新しい線がデータによりよく適合することがわかります。

全体的に、 MSE 小さくなっている…

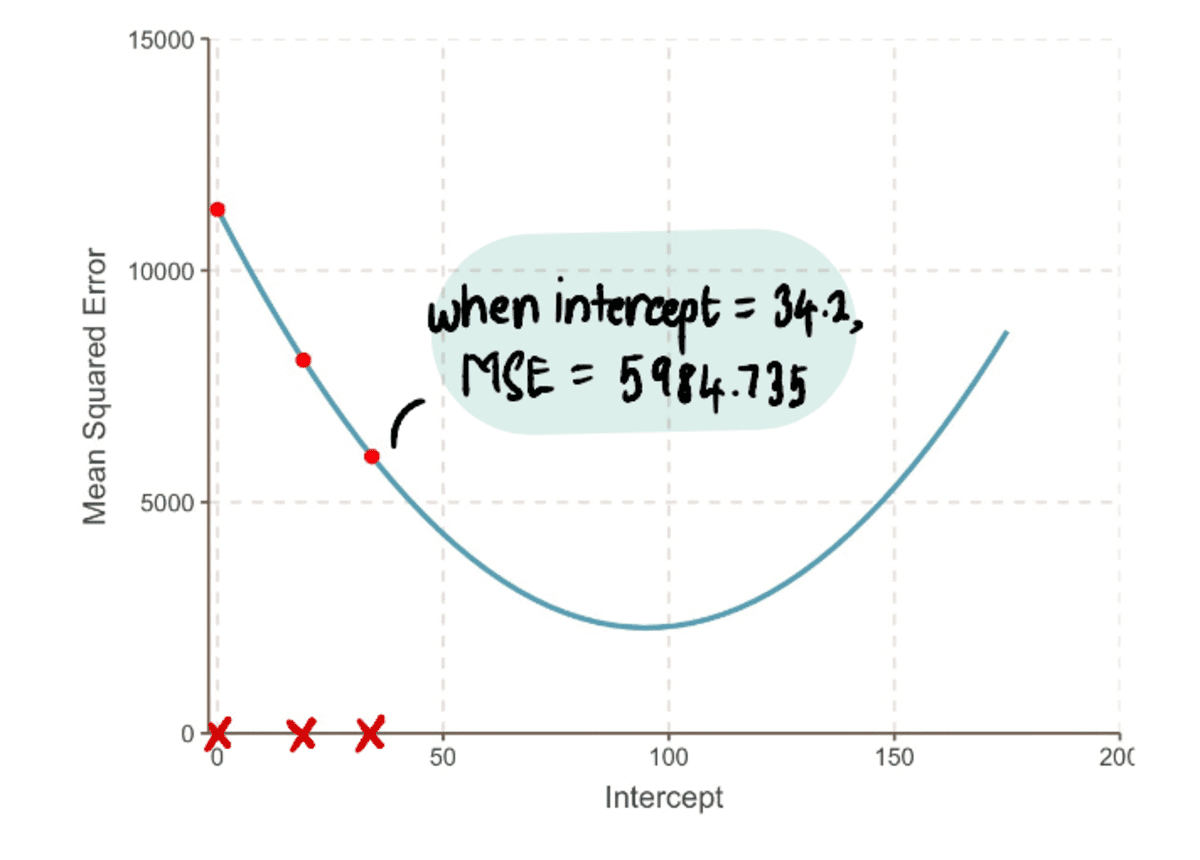
…そして私たちの ステップ サイズ 小さくなっています:

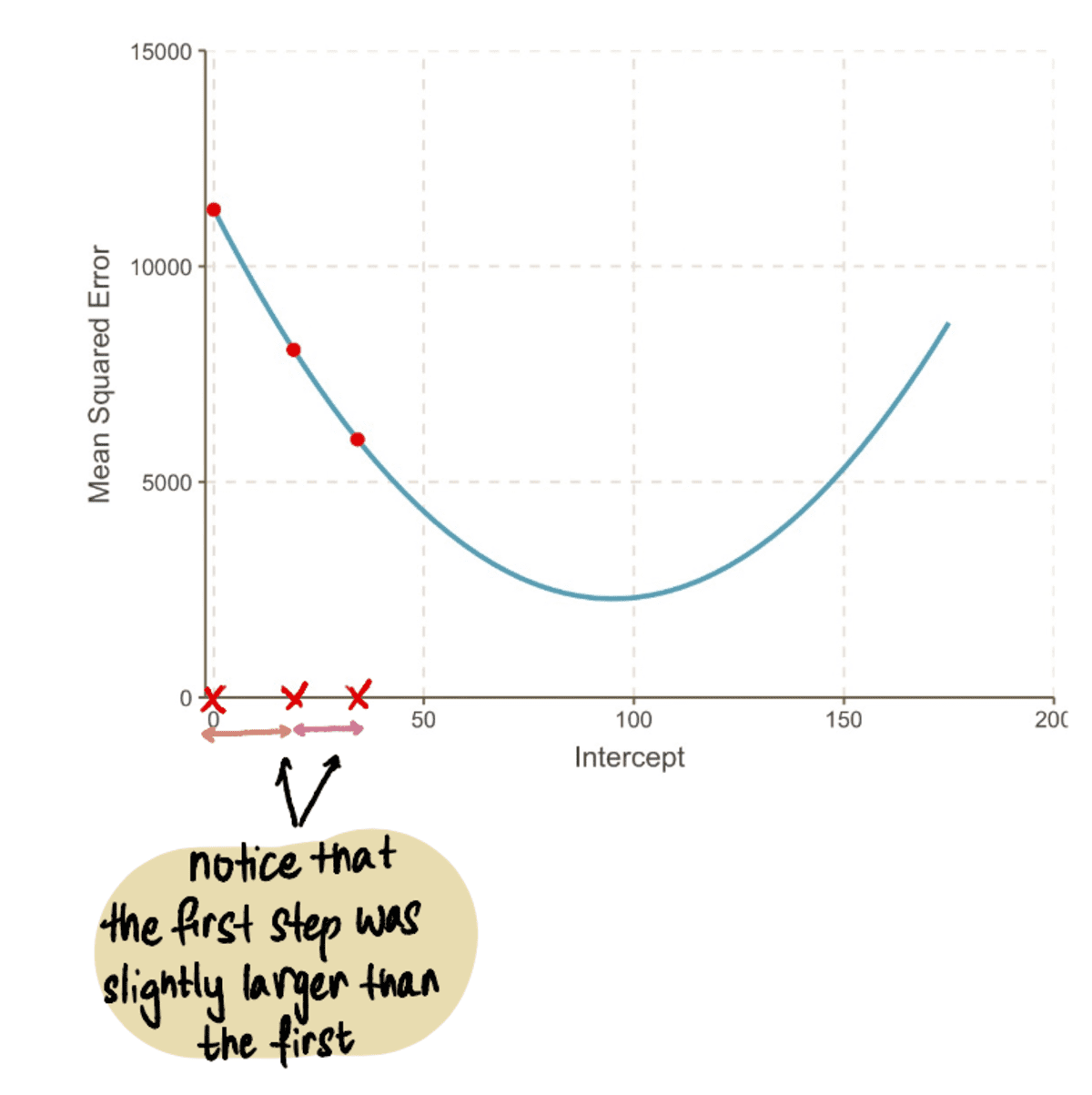
最適解に収束するまで、このプロセスを繰り返します。

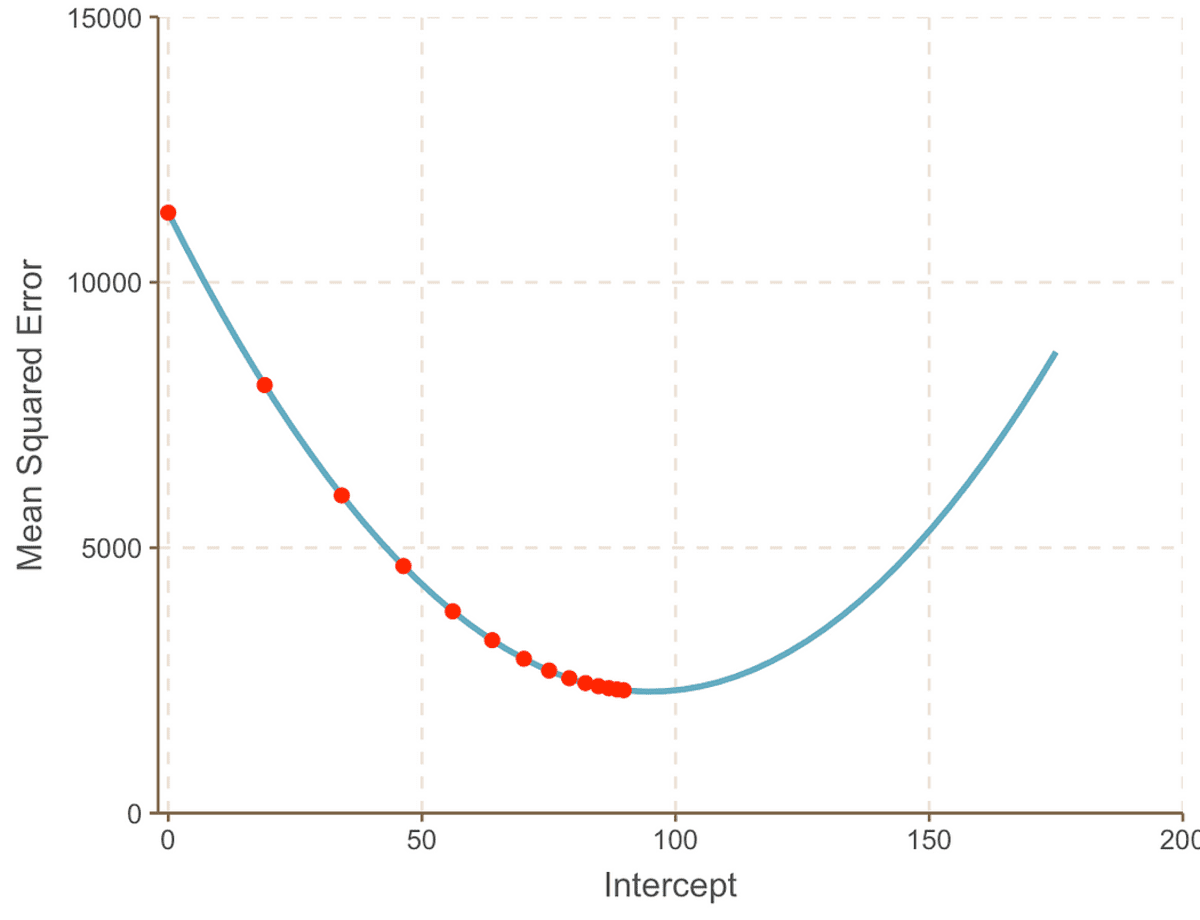
曲線の最小点に向かって進むと、 刻み幅 ますます小さくなる。 13 ステップの後、勾配降下アルゴリズムは インターセプト 値は 95 になります。水晶玉があれば、これが最小点として確認されます。 MSE 曲線。 そして、この方法が、前に見たブルート フォース アプローチと比較していかに効率的であるかは明らかです。 前の記事.

今、私たちは私たちの最適な価値を持っています インターセプト、線形回帰モデルは次のとおりです。

線形回帰直線は次のようになります。

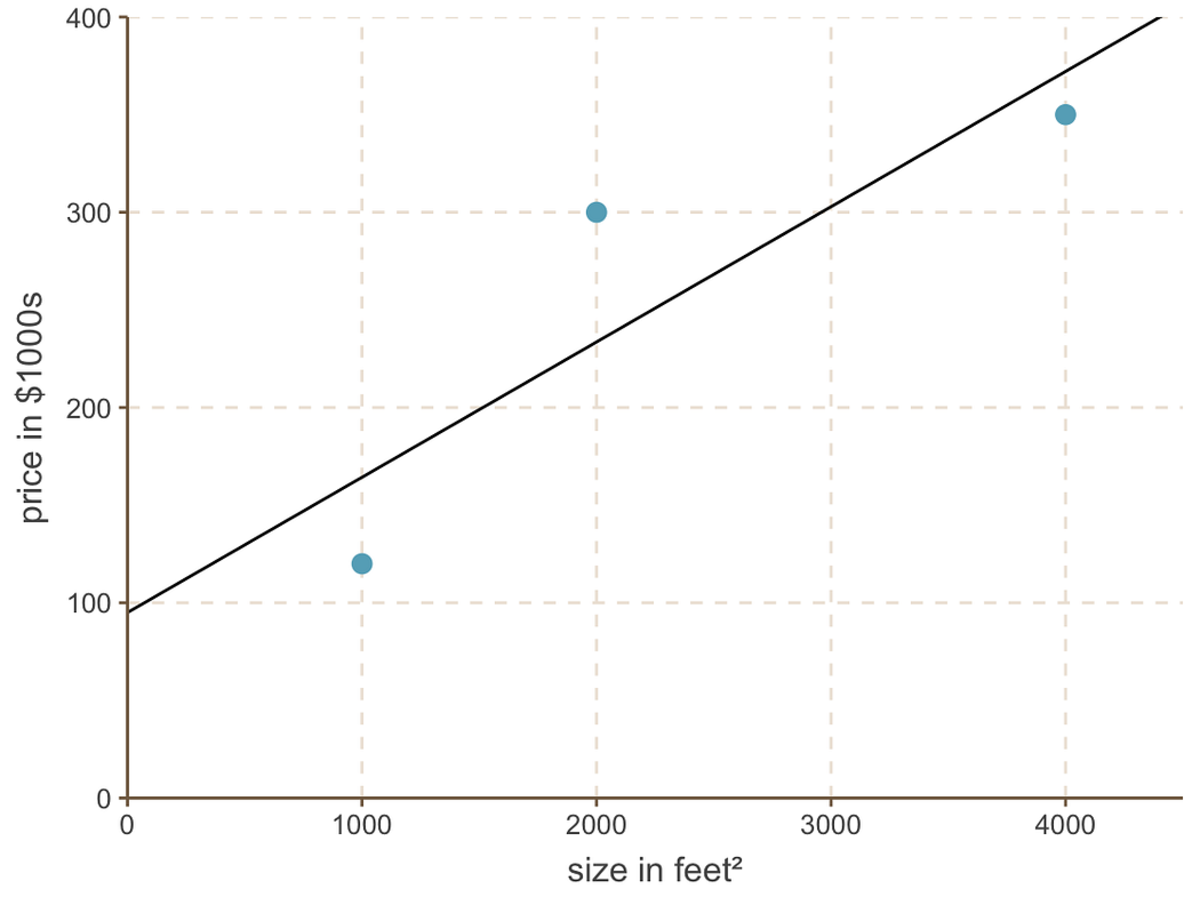
切片 = 95、勾配 = 0.069 の最適な直線

最後に、私たちの友人であるマークの質問に戻ります。

2400 フィート² の家のサイズを上記の式に代入します…

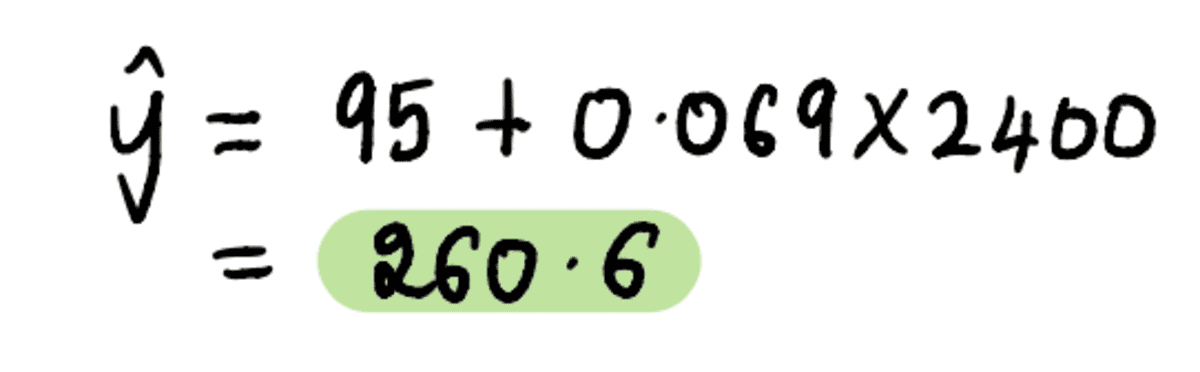
…そして出来上がり。 不必要に心配している友人のマークに、近所にある 3 つの家に基づいて、約 260,600 ドルで家を売ることを検討すべきだと伝えることができます。

概念をしっかりと理解したところで、長引く質問に答える簡単な Q&A セッションを行いましょう。

勾配を見つけることが実際に機能するのはなぜですか?

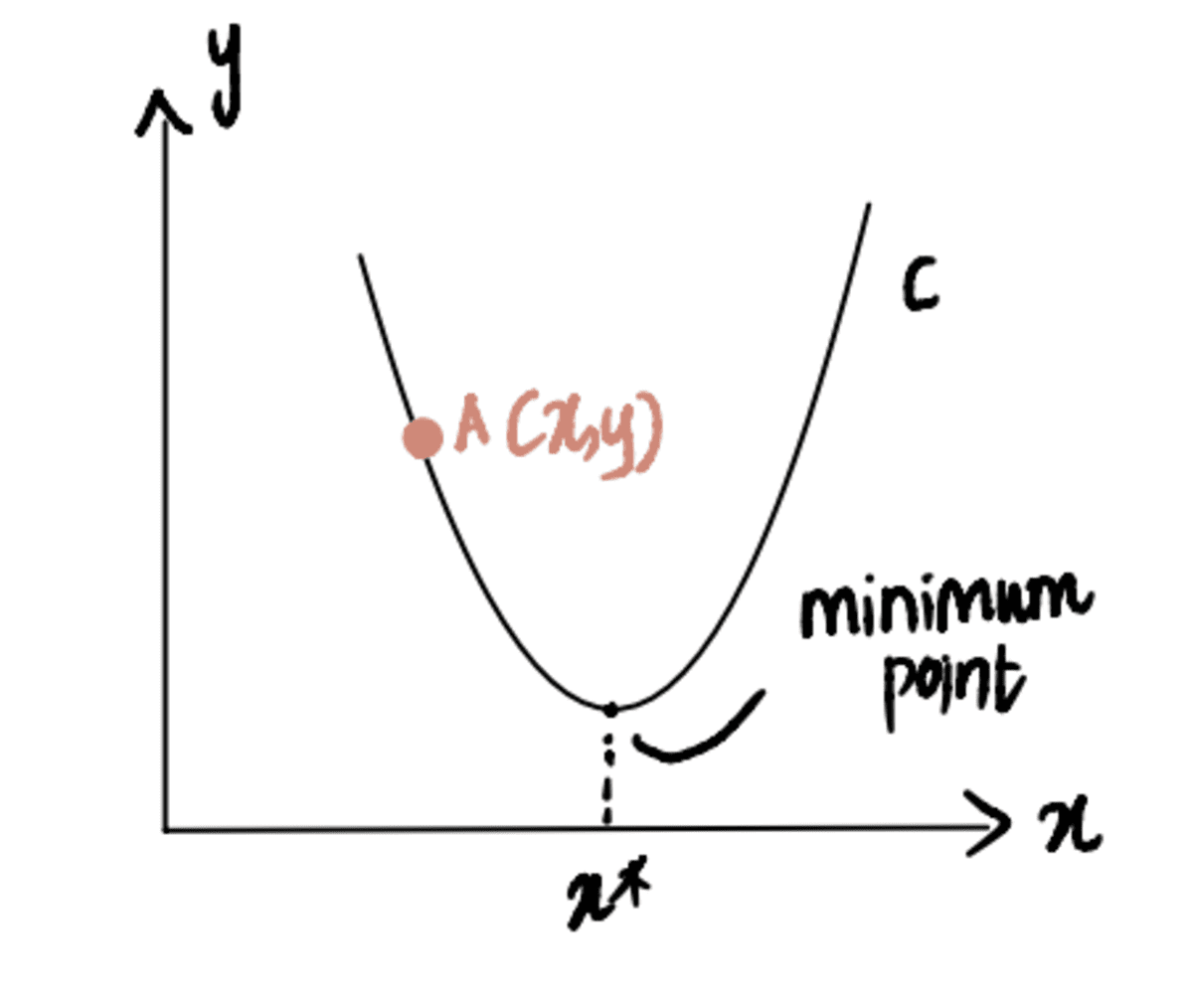
これを説明するために、次のように示される曲線 C の最小点に到達しようとしているシナリオを考えてみましょう。 x*. そして、私たちは現在点Aにいます x、左側にあります x*:

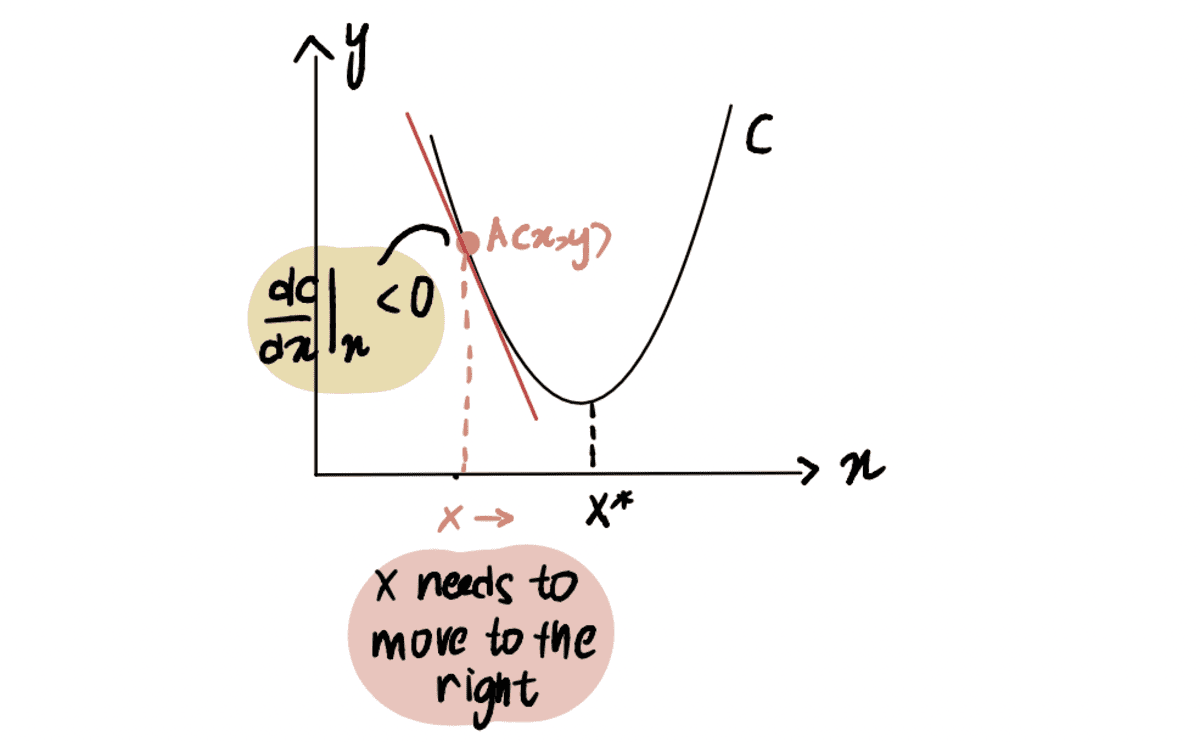
に関して点 A で曲線の微分を取ると、 x、次のように表されます dC(x)/dx、負の値を取得します (これは、 勾配 下に傾いています）。 また、到達するには右に移動する必要があることもわかります x*. したがって、私たちは増やす必要があります x 最低限に到達する バツ*。

赤い線またはグラデーションが下向きに傾斜している => 負のグラデーション

Since dC(x)/dx 否定的です x-??*dC(x)/dx より大きくなります x、したがってに向かって移動 x*.

同様に、最小点 x* の右側にある点 A にいる場合、 正の 勾配 (勾配 上に傾斜しています）、 dC(x)/dx.

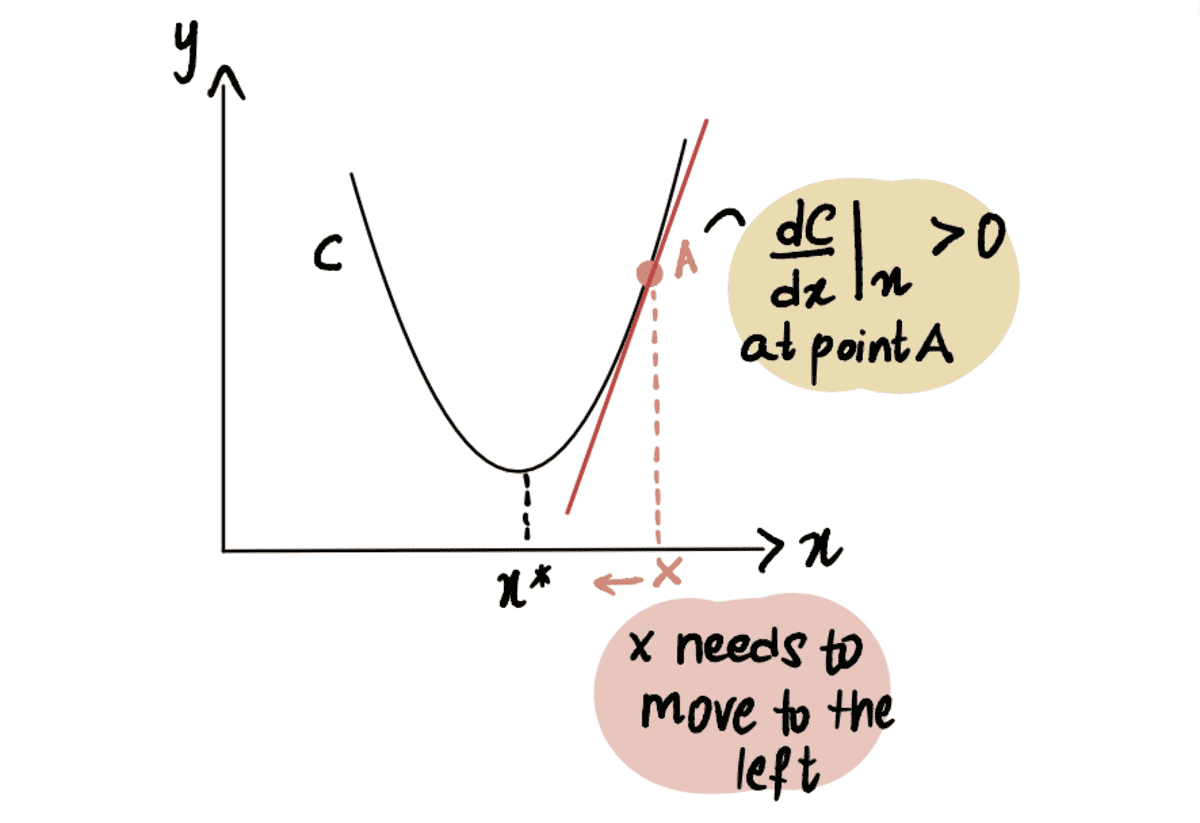
赤い線、またはグラデーションが上向きに傾斜している => 正のグラデーション

So x-??*dC(x)/dx 未満になります x、したがってに向かって移動 x*.

勾配まともな人は、歩みを止めるタイミングをどのように知っていますか?

勾配降下は、 刻み幅 は 0 に非常に近いです。前述のように、最小点では 勾配 は 0 であり、最小値に近づくと、 勾配 0 に近づきます。したがって、 勾配 点が 0 に近いか、最小点の近くにある場合、 刻み幅 も 0 に近くなり、アルゴリズムが最適解に到達したことを示します。

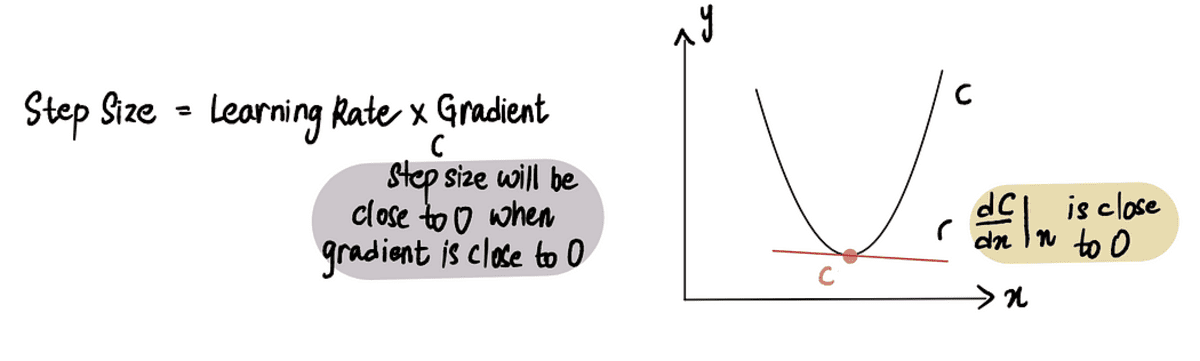
最小点に近づくと、勾配は 0 に近づき、その後、ステップ サイズは 0 に近づきます

実際には、最小ステップ サイズ = 0.001 以下

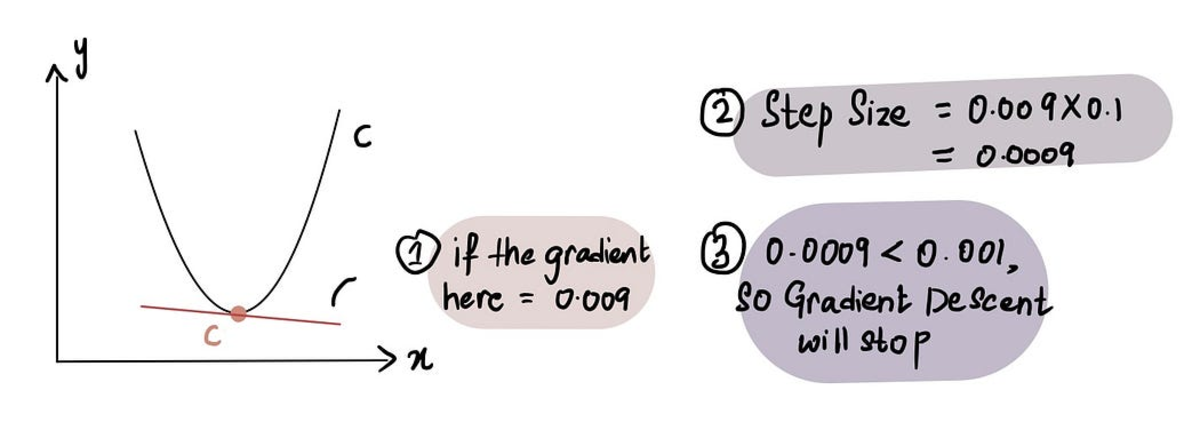
そうは言っても、勾配降下には、あきらめるまでにかかるステップ数の制限も含まれています。 最大ステップ数.

実際には、最大ステップ数 = 1000 以上

だからたとえ 刻み幅 より大きい 最小ステップ サイズ、それ以上の場合 最大ステップ数、勾配降下が停止します。

最小点を特定するのがより困難な場合はどうすればよいでしょうか?

これまでは、極小点を特定しやすい曲線で作業してきました (この種の曲線は、  ）。 しかし、それほどきれいではない曲線がある場合はどうなるでしょうか (技術的には 非凸) で、次のようになります。

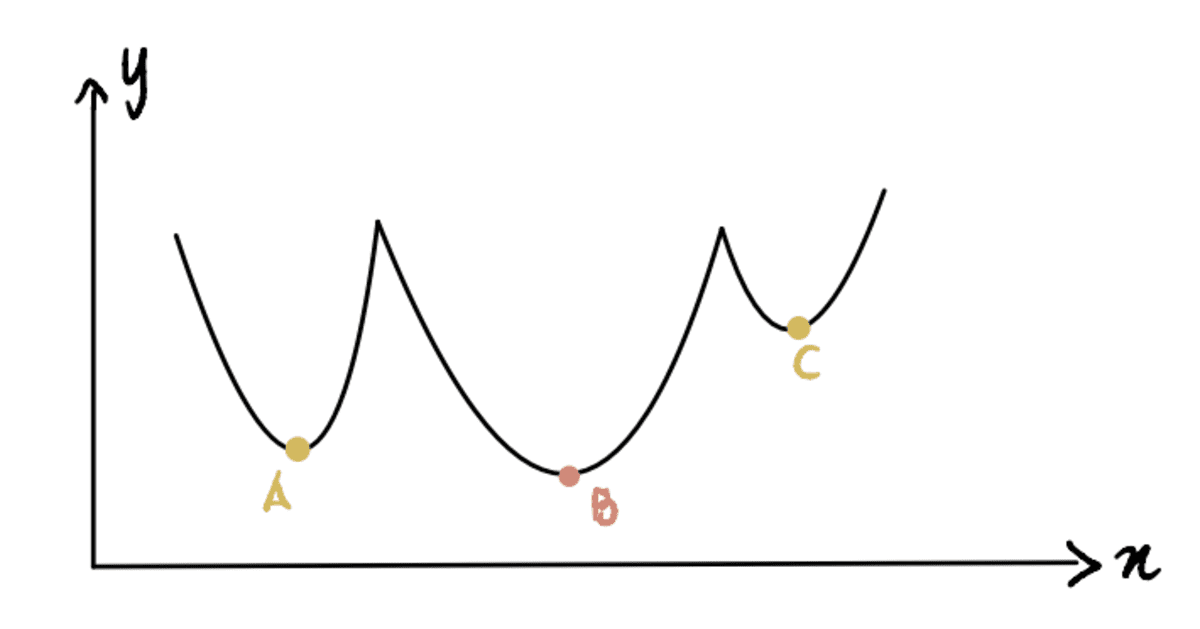
ここで、点 B が グローバルミニマム (実際の最小値) であり、点 A と点 C は ローカル最小値 （混同しやすいポイント グローバルミニマム しかしそうではありません）。 したがって、関数に複数の ローカル最小値 フォルダーとその下に グローバルミニマム、勾配降下法が見つけることは保証されていません グローバルミニマム. さらに、どの極小値を見つけるかは、最初の推測の位置によって異なります ( ステップ 1 勾配降下の）。

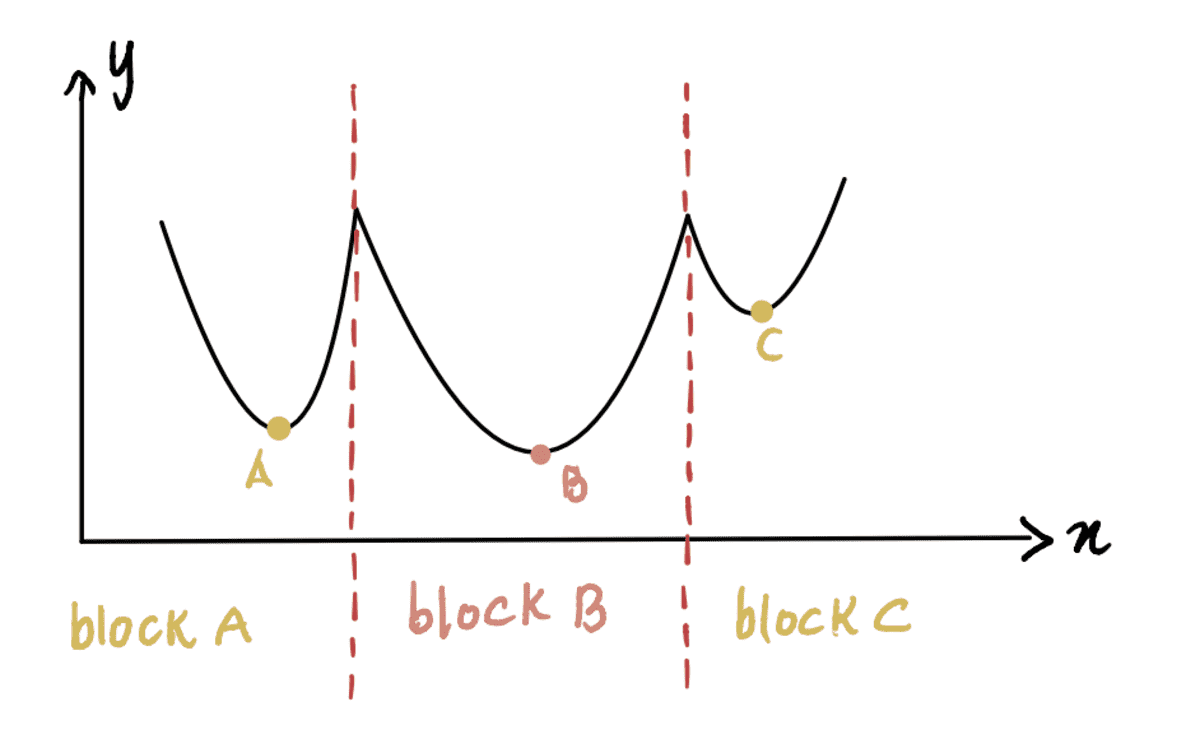
上記の非凸曲線を例にとると、最初の推測がブロック A またはブロック C にある場合、勾配降下法は、最小点が実際には B にあるときに、それぞれ極小点 A または C にあると宣言します。最初の推定がブロック B にある場合、アルゴリズムはグローバル最小 B を見つけます。

問題は、どのようにすれば適切な初期推測を行うことができるかということです。

簡単な答え： 試行錯誤。 すこし。

それほど単純ではない答え: 上のグラフから、 x これはブロック A にあるため 0 であり、局所最小値 A につながります。したがって、ご覧のとおり、ほとんどの場合、0 は適切な初期推定値ではない可能性があります。 一般的な方法は、x のすべての可能な値の範囲の一様分布に基づいてランダム関数を適用することです。 さらに、可能であれば、異なる初期推定値でアルゴリズムを実行し、それらの結果を比較すると、推定値が互いに大きく異なるかどうかについての洞察を得ることができます。 これは、グローバル最小値をより効率的に特定するのに役立ちます。

よし、あと少しだ。 最後の質問。

複数の最適値を見つけようとしている場合はどうなるでしょうか。

これまでは、最適なインターセプト値を見つけることだけに集中していました。 スロープ 線形回帰の値は 0.069 です。 しかし、水晶玉がなく、最適な方法がわからない場合はどうなりますか? スロープ 価値？ 次に、次のように表される勾配と切片の両方の値を最適化する必要があります。 x? および x? 。

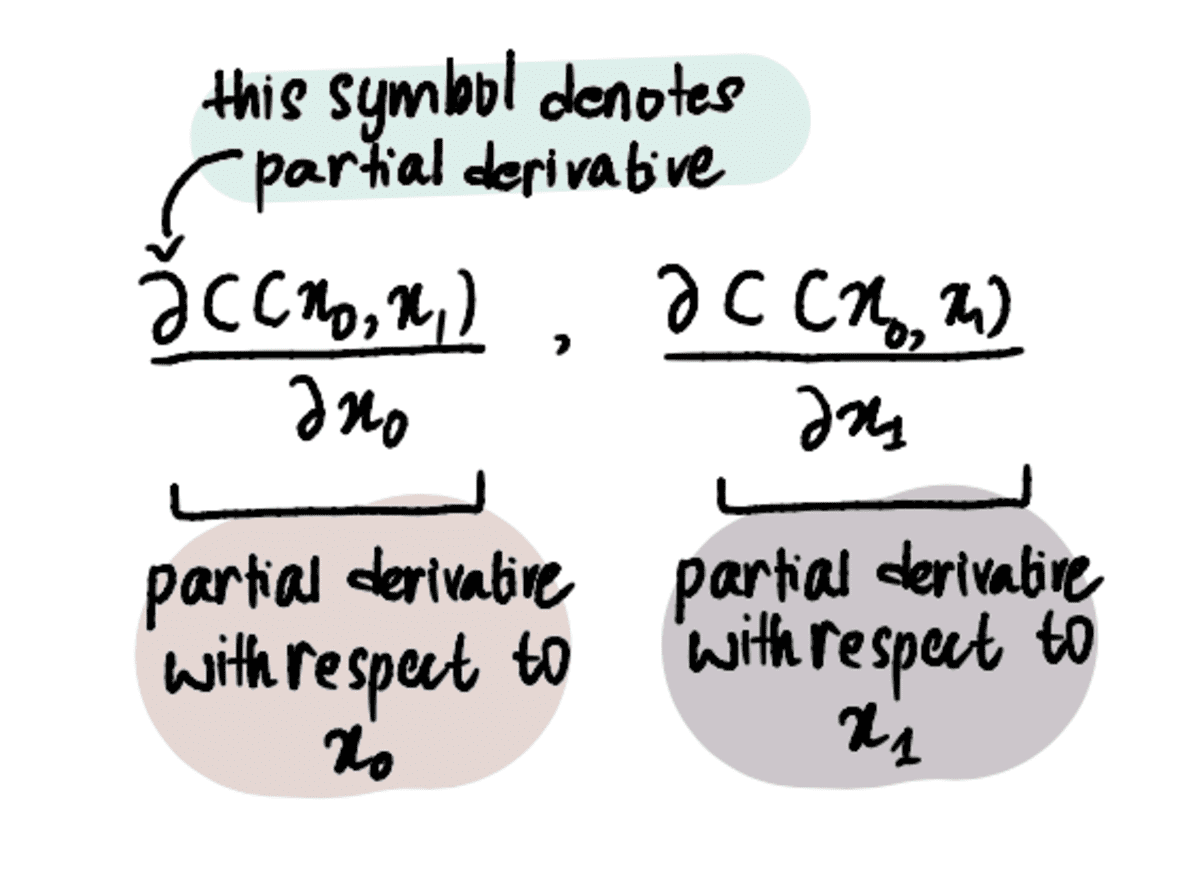
そのためには、導関数だけでなく、部分導関数を使用する必要があります。

注: 部分導関数は通常の古い導関数と同じ方法で計算されますが、最適化しようとしている変数が複数あるため、別の方法で示されます。 それらの詳細については、こちらをお読みください 記事 またはこれを見る ビデオ.

ただし、このプロセスは、単一の値を最適化するプロセスと比較的似ています。 コスト関数 ( MSE) を定義し、勾配降下アルゴリズムを適用する必要がありますが、両方の x? の偏導関数を見つけるステップが追加されています。 と×？

ステップ 1: x₀ と x₁ の初期推定を行う

ステップ 2: これらの点における x₀ と x₁ に関する偏導関数を見つけます。

ステップ 3: 偏導関数と学習率に基づいて x₀ と x₁ を同時に更新する

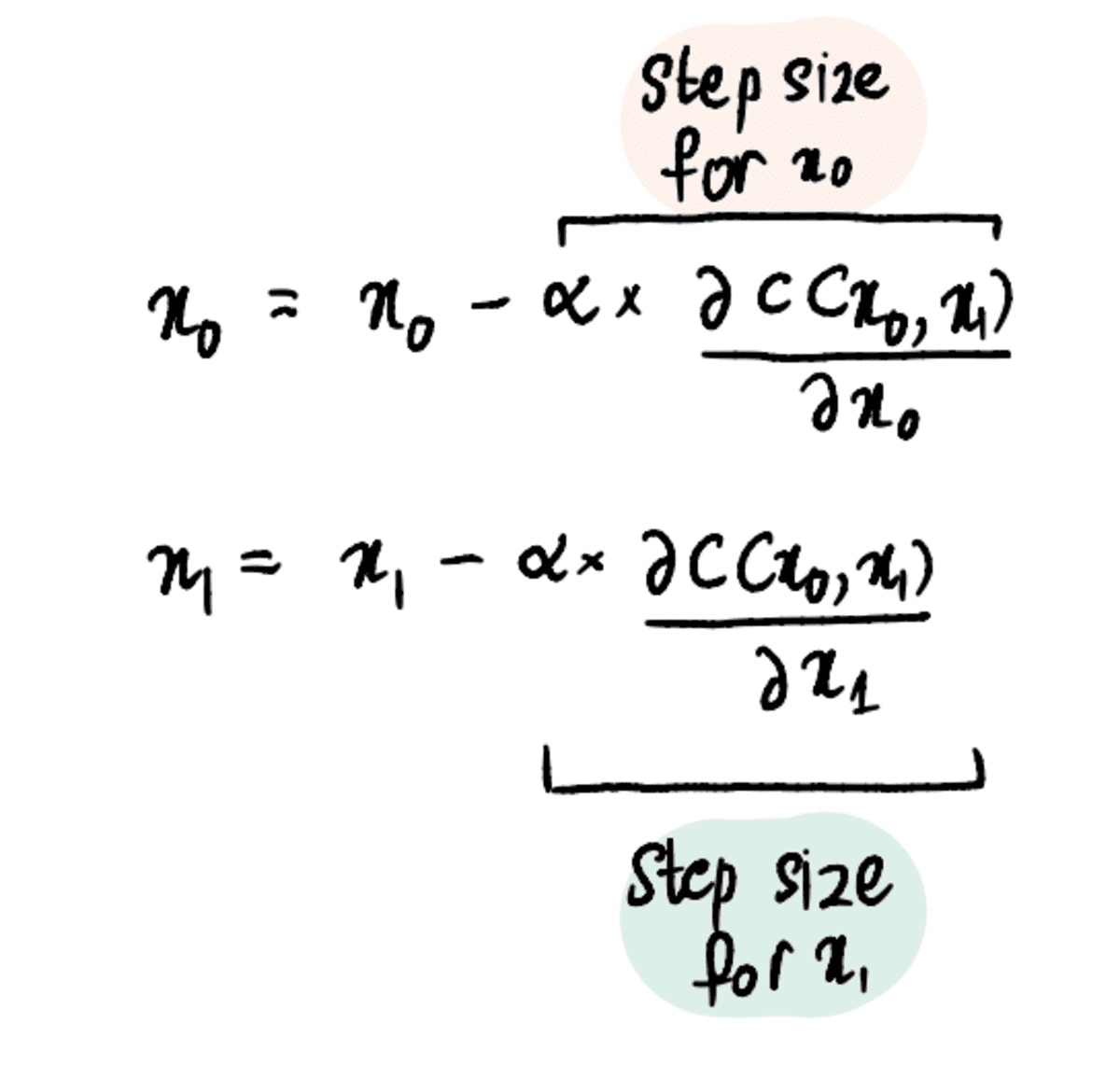
ステップ 4: 最大ステップ数に達するか、ステップ サイズが最小ステップ サイズよりも小さくなるまで、ステップ 2 ～ 3 を繰り返します。

そして、これらのステップを 3、4、または 100 の値に推定して最適化することができます。

結論として、勾配降下法は、最適な値に効率的に到達するのに役立つ強力な最適化アルゴリズムです。 勾配降下アルゴリズムは、他の多くの最適化問題に適用できるため、データ サイエンティストが武器庫に持つ基本的なツールとなっています。 より大きく、より優れたアルゴリズムに移行しましょう!

 
 
シュレヤ・ラオ 素人の言葉で機械学習アルゴリズムを図示し、説明します。

 
元の。 許可を得て転載。
 

• SEO を活用したコンテンツと PR 配信。 今日増幅されます。
• Platoblockchain。 Web3メタバースインテリジェンス。 知識の増幅。 こちらからアクセスしてください。
• 情報源： https://www.kdnuggets.com/2023/03/back-basics-part-dos-gradient-descent.html?utm_source=rss&utm_medium=rss&utm_campaign=back-to-basics-part-dos-gradient-descent