概要
この記事では、 仮説検定、帰無仮説と対立仮説の定式化、仮説検定の設定に焦点を当て、パラメトリック テストとノンパラメトリック テストについて深く掘り下げ、それぞれの仮定と Python での実装について説明します。ただし、私たちの主な焦点は、マン-ホイットニー U 検定やクラスカル-ウォリス検定などのノンパラメトリック検定です。最後には、仮説検定と、これらの概念を独自の統計分析に適用するための実践的なツールについて包括的に理解できるようになります。
学習目標
- 帰無仮説と対立仮説の定式化を含む、仮説検定の原理を理解します。
- 仮説テストの設定。
- パラメトリック テストとその種類について理解します。
- ノンパラメトリック テストとその型、およびその実装について理解します。
- パラメトリックとノンパラメトリックの違い。
目次
仮説検定とは何ですか?
仮説とは、個人または組織によって立てられた主張です。通常、この主張は平均や割合などの母集団パラメータに関するものであり、その主張を裏付ける証拠をサンプルから求めます。
仮説検定は、有意性検定とも呼ばれ、サンプルで測定されたデータを使用して母集団内のパラメーターに関する主張または仮説を確認する方法です。この方法を使用して、母集団パラメータ仮説が真であった場合に標本統計量が選択された可能性を判断することで、いくつかの理論を調査します。
仮説テストでは、次の 2 つの仮説を立てる必要があります。
- 帰無仮説 (H0)
- 対立仮説 (H1)
帰無仮説 : これは通常、差異がない仮説であり、通常は H0 で表されます。 RA Fisher によると、帰無仮説は、それが真であるという仮定の下で棄却の可能性についてテストされる仮説です (数学統計の基礎を参照)。
対立仮説: 帰無仮説を補完する仮説は対立仮説と呼ばれ、通常は H1 で示されます。
仮説検定の目的は、帰無仮説を棄却または保持して 2 つの変数 (通常は 1 つの独立変数と 1 つの従属変数、つまり通常 1 つは原因で 1 つは結果) 間の統計的に有意な関係を確立することです。
仮説テストのセットアップ
- 仮説を言葉で説明するか、主張します。
- 主張に基づいて帰無仮説と対立仮説を定義します。
- 上記の主張に適した仮説検定の種類を特定します。
- 帰無仮説の妥当性をテストするために使用する検定統計量を特定します。
- 帰無仮説の棄却および保持の基準を決定します。これは有意値と呼ばれ、伝統的に記号 α (アルファ) で表されます。
- 帰無仮説が真である場合に検定統計値を観察する条件付き確率である p 値を計算します。簡単に言えば、p 値は帰無仮説を裏付ける証拠です。
パラメトリックテストとノンパラメトリックテスト
ノンパラメトリック統計検定は、データのサンプリング元となる母集団分布のパラメーターに関する仮定に依存しませんが、パラメトリック統計検定は依存します。
パラメトリックテスト
ほとんどの統計的テストは、一連の仮定を基礎として使用して実行されます。特定の前提に違反すると、分析により誤解を招く結論または完全に誤った結論が得られる可能性があります。
通常、仮定は次のとおりです。
- 正規性: テストされるパラメータの標本分布は正規 (または少なくとも対称) 分布に従います。
- 分散の均一性: 2 つの異なる母集団からの母平均を検定しない限り、データの分散は異なるグループ間で同じです。
パラメトリック テストの一部は次のとおりです。
- Z 検定: 母集団の標準偏差がわかっている場合は、母集団の平均、分散、または比率を検定します。
- 学生の t 検定: 母集団の標準偏差が不明な場合は、母集団の平均、分散、または比率を検定します。
- 対応のある t 検定: 関連する 2 つのグループまたは条件の平均を比較するために使用されます。
- 分散分析 (ANOVA): 3 つ以上の独立したグループの平均を比較するために使用されます。
- 回帰分析: 1 つ以上の独立変数と従属変数の間の関係を評価するために使用されます。
- 共分散分析 (ANCOVA): 追加の共変量を分析に組み込むことで ANOVA を拡張します。
- 多変量分散分析 (MANOVA): ANOVA を拡張して、グループ間の複数の従属変数の差を評価します。
それでは、ノンパラメトリックテストについて詳しく見ていきましょう。
ノンパラメトリックテスト
ウォルフォウィッツは 1942 年に初めて「ノンパラメトリック」という用語を使用しました。ノンパラメトリック統計の概念を理解するには、まず、先ほど説明したパラメトリック統計の基本を理解する必要があります。あ パラメトリックテスト 特定の分布 (通常は正規分布) に従うサンプルが必要です。さらに、ノンパラメトリック検定は、正規性などのパラメトリック仮定から独立しています。
ノンパラメトリック テスト (母集団の分布に関する仮定がないため、分布フリー テストとも呼ばれます)。ノンパラメトリック テストは、データがデータから抽出されるという前提にテストが基づいていないことを意味します。 確率分布 平均、割合、標準偏差などのパラメータによって定義されます。
ノンパラメトリック検定は、次のいずれかの場合に使用されます。
- この検定は、平均や割合などの母集団パラメータに関するものではありません。
- この方法では、母集団の分布に関する仮定 (母集団が正規分布に従うなど) を必要としません。
ノンパラメトリックテストの種類
ここで、カイ二乗検定、マン・ホイットニー検定、ウィルコクソン符号順位検定、およびクラスカル・ウォリス検定を実行するための概念と手順について説明します。
カイ二乗検定
2 つの質的変数間の関連が統計的に有意であるかどうかを判断するには、カイ二乗検定と呼ばれる有意性検定を実行する必要があります。
カイ二乗検定には主に 2 つのタイプがあります。
カイ二乗適合度
適合度検定を使用して、未知の分布を持つ母集団が既知の分布に「適合」するかどうかを判断します。この場合、単一の定性調査の質問、または単一の母集団からの実験の単一の結果が存在します。適合度は通常、母集団が一様であるか (すべての結果が同じ頻度で発生する)、母集団が正規であるか、または母集団が既知の分布を持つ別の母集団と同じであるかを確認するために使用されます。帰無仮説と対立仮説は次のとおりです。
- H0: 母集団は指定された分布に適合します。
- Ha: 母集団は指定された分布に適合しません。
例を挙げて理解しましょう
| 日付 | 月曜日 | 火曜日 | Wednesday | 木曜日 | 金曜日 | 土曜日 | 日曜日 |
| 故障数 | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
表には、因子内の内訳の数が表示されます。この例では変数が 1 つだけあり、観測された分布 (表に示されている) が期待される分布に適合するかどうかを判断する必要があります。
このため、帰無仮説と対立仮説は次のように定式化されます。
- H0:内訳は均一に分布しています。
- Ha: 内訳は均一に分布していません。
そして、自由度は n-1 になります (この場合、 n=7 、つまり df = 7-1=6)
Expected value will be= (14+22+16+18+12+19+11)/7=16
| 日付 | 月曜日 | 火曜日 | Wednesday | 木曜日 | 金曜日 | 土曜日 | 日曜日 |
| 故障数(実測) | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
| 予想される | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| (観測値 - 期待値) | -2 | 6 | 0 | 2 | -4 | 3 | -5 |
| (観測値 - 期待値)^2 | 4 | 36 | 0 | 4 | 16 | 9 | 25 |
この式を使用してカイ 2 乗を計算します
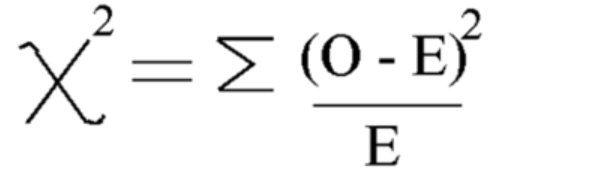
カイ二乗 = 5.875
自由度は = n-1=7-1=6 となります。
ここでクリティカル値を見てみましょう カイ二乗分布表 5 % の有意水準で
したがって、臨界値は 12.592 です。
カイ二乗計算値が臨界値 より小さいため、帰無仮説を受け入れ、内訳は均一に分布していると結論付けることができます。
検定のカイ二乗の独立性
独立性検定を使用して、2 つの変数 (因子) が独立しているか依存しているか、つまり、これら 2 つの変数間に有意な関連関係があるかどうかを判断します。この場合、2 つの定性調査質問または実験があり、分割表が作成されます。目的は、2 つの変数が無関係 (独立) であるか、関連している (依存) かを確認することです。帰無仮説と対立仮説は次のとおりです。
- H0: 2 つの変数 (因子) は独立しています。
- Ha: 2 つの変数 (因子) は依存関係にあります。
例を見てみましょう
性別とシャツの好みの色が独立しているかどうかを調べたい例。これは、人の性別が色の選択に影響を与えるかどうかを知りたいことを意味します。アンケートを実施し、データを表に整理しました。
この表は観測値です。
| ブラック | ホワイト | レッド | 青 | |
| 男性 | 48 | 12 | 33 | 57 |
| 女性 | 34 | 46 | 42 | 26 |
ここで、まず帰無仮説と対立仮説を立てます
- H0: 性別と好みのシャツの色は独立しています
- Ha: 性別と好みのシャツの色は独立していません
カイ二乗検定統計量を計算するには、期待値を計算する必要があります。したがって、すべての行と列と全体の合計を追加します。
| ブラック | ホワイト | レッド | 青 | トータル | |
| 男性 | 48 | 12 | 33 | 57 | 150 |
| 女性 | 34 | 46 | 42 | 26 | 148 |
| トータル | 82 | 58 | 75 | 83 | 298 |
この後、次の式 = (行の合計 * 列の合計)/全体の合計を使用して、各エントリについて上の表から期待値テーブルを計算できます。
期待値表:
| ブラック | ホワイト | レッド | 青 | |
| 男性 | 41.3 | 29.2 | 37.8 | 41.8 |
| 女性 | 40.7 | 28.8 | 37.2 | 41.2 |
次に、カイ二乗検定の公式を使用してカイ二乗値を計算します。
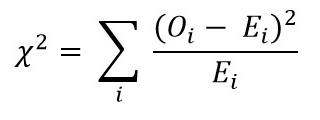
- Oi = 観測値
- ei = 期待値
得られる値は次のとおりです: Χ2 = 34.9572
自由度の計算
DF=(行-1の数)*(列-1の数)
次に、臨界値を見つけてカイ二乗検定と比較します。 統計値:
これを行うには、次から自由度と有意水準 (アルファ) を調べることができます。 カイ二乗分布表
アルファ =0.050 では、臨界値 = 7.815 が得られます。
カイ二乗>臨界値であるため
したがって、帰無仮説を棄却し、性別と好みのシャツの色は独立していないと結論付けることができます。
カイ二乗の実装
ここで、Python での実際の例を使用してカイ 2 乗の実装を見てみましょう。
- H0: 性別と好みのシャツの色は独立しています
- Ha: 性別と好みのシャツの色は独立していません
データセットの作成:
import pandas as pd
from scipy.stats import chi2_contingency
from scipy.stats import chi2
# Given dataset
df_dict = {
'Black': [48, 34],
'White': [12, 46],
'Red': [33, 42],
'Blue': [57, 26]
}
dataset_table = pd.DataFrame(df_dict, index=['Male', 'Female'])
print("Dataset Table:")
print(dataset_table)
print()
# Observed Values
Observed_Values = dataset_table.values
print("Observed Values:")
print(Observed_Values)
print()
# Perform chi-square test
val = chi2_contingency(dataset_table)
Expected_Values = val[3]
print("Expected Values:")
print(Expected_Values)
print()
# Degree of Freedom
no_of_rows = len(dataset_table.iloc[0:2, 0])
no_of_columns = 4
ddof = (no_of_rows - 1) * (no_of_columns - 1)
print("Degree of Freedom:", ddof)
print()
# Chi-square statistic
chi_square = sum([(o - e) ** 2. / e for o, e in zip(Observed_Values, Expected_Values)])
chi_square_statistic = chi_square[0] + chi_square[1]
print("Chi-square statistic:", chi_square_statistic)
print()
# Critical value
alpha = 0.05
critical_value = chi2.ppf(q=1-alpha, df=ddof)
print('Critical value:', critical_value)
print()
# p-value
p_value = 1 - chi2.cdf(x=chi_square_statistic, df=ddof)
print('p-value:', p_value)
print()
# Significance level
print('Significance level:', alpha)
print('p-value:', p_value)
print('Degree of Freedom:', ddof)
print()
# Hypothesis testing
if chi_square_statistic >= critical_value:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
print()
if p_value <= alpha:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
出力:
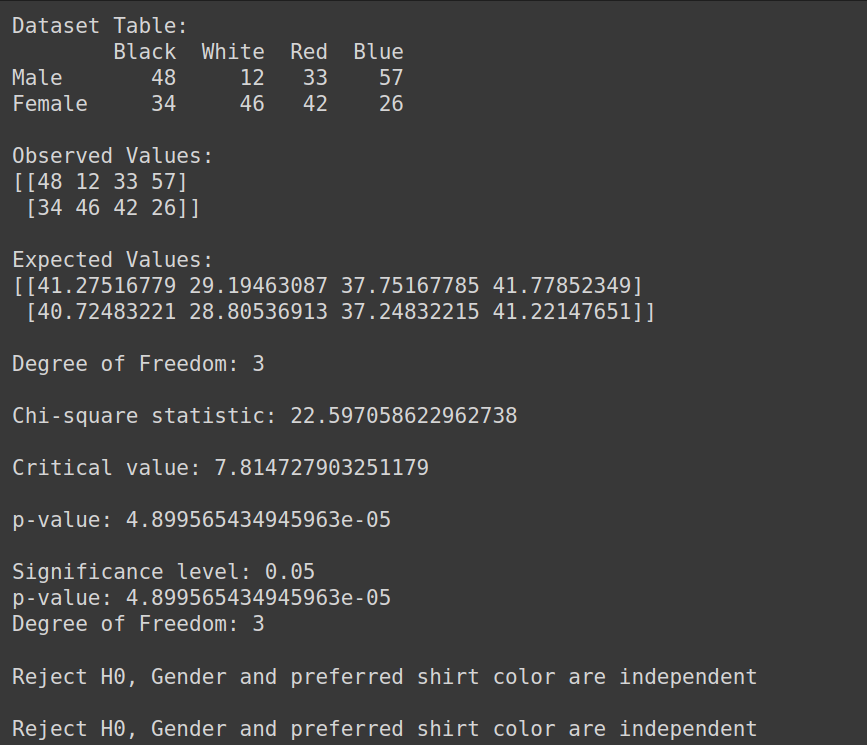
マン・ホイットニー U 検定
マン-ホイットニー U 検定は、独立サンプル t 検定のノンパラメトリック代替として機能します。同じ母集団からの 2 つのサンプル平均を比較し、それらが等しいかどうかを判断します。この検定は通常、順序データ、または t 検定の仮定が満たされない場合に使用されます。
マン-ホイットニー U 検定では、両方のグループのすべての値を一緒にランク付けし、各グループのランクを合計します。これらのランクに基づいて検定統計量 U を計算します。 U 統計は、テーブルの臨界値と比較されるか、近似値を使用して計算されます。 U 統計量が臨界値より小さい場合、帰無仮説は棄却されます。
これは、平均を比較して正規分布を仮定する t 検定のようなパラメトリック検定とは異なります。代わりに、マン-ホイットニー U 検定ではランクが比較され、正規分布の仮定は必要ありません。
マン-ホイットニー U 検定は、結果がグループ平均の差ではなくグループ順位の差で表示されるため、理解するのが難しい場合があります。
マン・ホイットニー検定の公式:
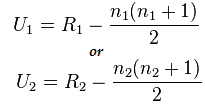
U= 分(U1,U2)
ここでは、
- U= マン・ホイットニーの U 検定
- n1= サンプルサイズ XNUMX
- n2= サンプルサイズ XNUMX
- R1= サンプルサイズ XNUMX のランク
- R2= サンプルサイズ 2 のランク
それでは、短い例でこれを理解してみましょう。
患者の健康改善における 2 つの異なる治療法 (方法 A と方法 B) の有効性を比較したいとします。次のデータがあります。
- 方法 A: 3,4,2,6,2,5、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX
- 方法 B: 9,7,5,10,6,8、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX
ここでは、データが正規分布しておらず、サンプルサイズが小さいことがわかります。
マン・ホイットニー U 検定の実施
ここで、マン-ホイットニーの U 検定を実行してみましょう。
しかし、最初に帰無仮説と対立仮説を定式化しましょう
- H0:各治療のランクに差はありません
- Ha:各治療ごとにランクに差があります
すべての治療法を組み合わせる: 3,4,2,6,2,5,9,7,5,10,6,8、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX
ソート済みデータ:2,2,3,4,5,5,6,6,7,8,9,10
ソートされたデータのランク: 1,2,3,4,5,6,7,8,9,10,11,12、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX、XNUMX
- データを個別にランク付けします。
- Method A: 3(3),4(4),2(1.5),6(7.5),2(1.5),5(5.5)
- Method B: 9(11),7(9),5(5.5),10(12),6(1.5),8(10)
- ランクの合計を計算します):
- R1: 3+4+1.5+7.5+1.5+5.5=23
- R2: 11+9+5.5+12+1.5+10=55
次に、次の式を使用して統計値を計算します。
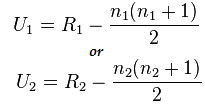
ここで、n1=6 および n2=6
U1=2、U2=34の計算後の値
U 統計の計算:
Us= 最小(U1,U2)= 最小(2,34)= 2
マン・ホイットニー表 臨界値を見つけることができます
この場合クリティカル値は5になります
Uc= 5 は 5% の有意水準で Us より大きいため、拒否します。 H0
したがって、各治療のランクには差があると結論付けることができます。
Pythonでの実装
from scipy.stats import mannwhitneyu, norm
import numpy as np
TreatmentA = np.array([3,4,2,6,2,5])
TreatmentB = np.array([9,7,5,10,6,8])
# Perform Mann-Whitney U test
U_statistic, p_value = mannwhitneyu(TreatmentA, TreatmentB)
# Print the result
print(f'The U-statistic is {U_statistic:.2f} and the p-value is {p_value:.4f}')
if p_value < 0.05:
print("Reject Null Hypothesis: There is a significant difference between the Rank of each treatment.")
else:
print("Fail to Reject Null Hypothesis: Fail to Reject Null Hypothesis: There is no enough evidence to conclude that there is difference between the Rank of each treatment")出力:

クラスカル – ウォリス テスト
Kruskal –Wallis テストは複数のグループで使用されます。これはノンパラメトリックであり、分散の正規性と等価性の仮定に違反した場合に一元配置分散分析検定に代わる貴重な代替手段です。クラスカル –ウォリス検定では、2 つ以上の独立したグループの中央値を比較します。
k 個の独立したサンプル (k>=3) が同一の分布を持つ母集団から抽出された場合に、母集団の正規性の条件を必要とせずに帰無仮説を検定します。
仮定:
少なくとも 5 つの独立して抽出されたランダム サンプルがあることを確認します。各サンプルには少なくとも 5 つの観測値が含まれます (n>=XNUMX)
3 つのグループの学生が使用した勉強方法が試験の得点に影響するかどうかを判断したい例を考えてみましょう。クラスカル・ウォリス検定を使用してデータを分析し、グループ間で試験のスコアに統計的に有意な差があるかどうかを評価できます。
これに対する帰無仮説を次のように定式化します。
- H0: 3 つのグループの学生の間で試験の得点に差はありません。
- Ha: 3 つのグループの学生の間では試験の得点に差があります。
ウィルコクソンの署名付き順位テスト
ウィルコクソン符号付き順位検定 (ウィルコクソン一致ペア検定とも呼ばれる) は、依存サンプル t 検定または対応のあるサンプル t 検定のノンパラメトリック バージョンです。符号検定は、対応のある標本の t 検定に代わるもう 1 つのノンパラメトリックな代替方法です。これは、対象となる変数が本質的に二分的である場合 (男性と女性、はいといいえなど) に使用されます。 Wilcoxon の符号付き順位検定も、1 サンプルの t 検定のノンパラメトリック バージョンです。ウィルコクソンの符号付き順位検定では、2 つの状況下でグループの中央値 (ペアのサンプル) を比較するか、グループの中央値と仮説の中央値 (1 つのサンプル) を比較します。
これを例で理解しましょう。8 週間のプログラムに参加する前と後の喫煙者の XNUMX 日のタバコ消費量に関するデータがあり、プログラムの前後で XNUMX 日のタバコ消費量に大きな違いがあるかどうかを判断したいとします。このテストを使用してください
これに対する仮説の立て方は次のようになります。
- H0: プログラムの前後で毎日のタバコの消費量に違いはありません。
- Ha:プログラムの前後で1日のタバコの消費量に違いがあります
正規性をテストする
ここで正規性テストについて説明しましょう。
シャピロ・ウィルク検査
Shapiro-Wilk 検定は、データの特定のサンプルが正規分布した母集団からのものであるかどうかを評価します。これは、正規性をチェックするために最も一般的に使用されるテストの 1 つです。このテストは、比較的小さいサンプル サイズを扱う場合に特に役立ちます。
シャピロ-ウィルクテストでは次のようになります。
- 帰無仮説 : サンプル データは、正規分布に従う母集団から取得されます。
- 対立仮説: サンプルデータは、正規分布に従う母集団から得られたものではありません。
Shapiro-Wilk 検定によって生成された検定統計量は、正規性の仮定の下で、観察されたデータと予想されるデータの間の差異を測定します。検定統計量に関連付けられた p 値が選択した有意水準 (たとえば、0.05) より小さい場合、帰無仮説は棄却され、データが正規分布していないことを示します。 p 値が有意水準より大きい場合、帰無仮説を棄却できず、データが正規分布に従う可能性があることが示唆されます。
まず、これらのテスト用のデータセットを作成しましょう。任意のデータセットを使用できます。
import pandas as pd
# Create the dictionary with the provided data
data = {
'population': [6.1101, 5.5277, 8.5186, 7.0032, 5.8598],
'profit': [17.5920, 9.1302, 13.6620, 11.8540, 6.8233]
}
# Create the DataFrame
df = pd.DataFrame(data)
response_var=df['profit']
Here, a sample for running Shapiro -Wilk test on python:
from scipy.stats import shapiro
stat, p_val = shapiro(response_var)
print(f'Shapiro-Wilk Test: Statistic={stat} p-value={p_val}')
if p_val > alpha:
print('Data looks normal (fail to reject H0)')
else:
print('Data looks normal (fail to reject H0)')出力:

この検定は、サンプル サイズが大きくなると信頼性が低くなるため、比較的小さなサンプル サイズ (n=< 50-2000) に最も適しています。
アンダーソン・ダーリン
データの特定のサンプルが正規分布などの指定された分布に由来するかどうかを評価します。これは Shapiro-Wilk テストに似ていますが、特にサンプルサイズが小さい場合に感度が高くなります。
これは、分布のパラメーターが不明な場合に、正規分布を含むいくつかの分布に適しています。
これを実装するための Python コードは次のとおりです。
from scipy.stats import anderson
response_var = data['profit']
alpha = 0.05
# Anderson-Darling Test
result = anderson(response_var)
print(f'Anderson statistics: {result.statistic:.3f}')
if result.statistic > result.critical_values[-1]:
p_value = 0.0 # The p-value is essentially 0 if the statistic exceeds the largest critical value
else:
p_value = result.significance_level[result.statistic < result.critical_values][-1]
print("P-value:", p_value)
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")出力:

ハルケ・ベラ・テスト
ハルケ・ベラ検定は、データの特定のサンプルが正規分布した母集団からのものであるかどうかを評価します。これはデータの歪度と尖度に基づいています。
サンプル データを使用した Python での Jarque-Bera テストの実装は次のとおりです。
from scipy.stats import jarque_bera
# Performing Jarque-Bera test
test_statistic, p_value = jarque_bera(response_var)
print("Jarque-Bera Test Statistic:", test_statistic)
print("P-value:", p_value)
# Interpreting results
alpha = 0.05
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")出力:

| カテゴリー | パラメトリック統計手法 | ノンパラメトリック統計手法別案内 |
| 相関 | ピアソン積モーメント相関係数 (r) | スピアマンの順位係数相関 (Rho)、ケンダルのタウ |
| 2 つのグループ、独立した対策 | 独立した t 検定 | マン・ホイットニーの U 検定 |
| 2 つ以上のグループ、独立した措置 | 一元配置分散分析 | クラスカル・ウォリス一元配置分散分析 |
| 2 つのグループ、反復測定 | 対応のある t 検定 | ウィルコクソンの一致ペアの符号付きランク テスト |
| 2 つ以上のグループ、反復測定 | 一元配置反復測定分散分析 | フリードマンの二元配置分散分析 |
まとめ
仮説検定 は、サンプル データを使用して母集団パラメータに関する主張を評価するために不可欠です。パラメトリック テストは特定の仮定に依存しており、間隔や比率のデータに適していますが、ノンパラメトリック テストはより柔軟で、厳密な分布の仮定を持たずに名目データや順序データに適用できます。 Shapiro-Wilk や Anderson-Darling などの検定は正規性を評価し、カイ 2 乗や Jarque-Bera は適合度を評価します。パラメトリック検定とノンパラメトリック検定の違いを理解することは、適切な統計的アプローチを選択するために重要です。全体として、仮説検証は、データに基づいた意思決定を行い、経験的証拠から信頼できる結論を引き出すための体系的なフレームワークを提供します。
高度な統計分析をマスターする準備はできていますか? 今すぐ BlackBelt データ分析コースに登録してください。 仮説テスト、パラメトリックおよびノンパラメトリック テスト、Python 実装などに関する専門知識を獲得します。統計スキルを高め、データに基づいた意思決定に優れます。今すぐ参加してください!
よくある質問
A. パラメトリック検定では、正規性や分散の均一性など、母集団の分布とパラメーターに関する仮定が行われますが、ノンパラメトリック検定はこれらの仮定に依存しません。パラメトリック テストは、仮定が満たされる場合に高い検出力を持ちますが、ノンパラメトリック テストはより堅牢で、データが歪んでいる場合や正規分布していない場合など、幅広い状況に適用できます。
A. カイ二乗検定は、2 つのカテゴリ変数間に有意な関連があるかどうかを判断するために使用されます。通常、カテゴリ データを分析し、分割表内の変数の独立性に関する仮説をテストします。
A. マン-ホイットニーの U 検定は、従属変数が順序変数であるか正規分布ではない場合に、2 つの独立したグループを比較します。 2 つのグループの中央値間に有意差があるかどうかを評価します。
A. Shapiro-Wilk 検定は、サンプルが正規分布した母集団からのものであるかどうかを評価します。データが正規分布に従うという帰無仮説を検定します。 p 値が選択した有意水準 (たとえば、0.05) より小さい場合、帰無仮説は棄却され、データは正規分布していないと結論付けられます。
- SEO を活用したコンテンツと PR 配信。 今日増幅されます。
- PlatoData.Network 垂直生成 Ai。 自分自身に力を与えましょう。 こちらからアクセスしてください。
- プラトアイストリーム。 Web3 インテリジェンス。 知識増幅。 こちらからアクセスしてください。
- プラトンESG。 カーボン、 クリーンテック、 エネルギー、 環境、 太陽、 廃棄物管理。 こちらからアクセスしてください。
- プラトンヘルス。 バイオテクノロジーと臨床試験のインテリジェンス。 こちらからアクセスしてください。
- 情報源: https://www.analyticsvidhya.com/blog/2024/04/a-comprehensive-guide-on-non-parametric-tests/



