Introductie
In dit artikel zullen we onderzoeken wat dat is hypothesetesten, met de nadruk op het formuleren van nul- en alternatieve hypothesen, het opzetten van hypothesetests en we zullen diep duiken in parametrische en niet-parametrische tests, waarbij we hun respectieve aannames en implementatie in Python bespreken. Maar onze belangrijkste focus zal liggen op niet-parametrische tests zoals de Mann-Whitney U-test en de Kruskal-Wallis-test. Aan het einde zul je een uitgebreid inzicht hebben in het testen van hypothesen en de praktische hulpmiddelen om deze concepten toe te passen in je eigen statistische analyses.
leerdoelen
- Begrijp de principes van het testen van hypothesen, inclusief het formuleren van nul- en alternatieve hypothesen.
- Hypothesetest opzetten.
- Inzicht in parametrische tests en de typen ervan.
- Inzicht in niet-parametrische tests en de typen ervan, samen met de implementatie ervan.
- Verschil tussen parametrisch en niet-parametrisch.
Inhoudsopgave
Wat is het testen van hypothesen?
Hypothese is een bewering van een persoon/organisatie. De claim gaat meestal over populatieparameters zoals gemiddelde of proportie, en we zoeken bewijs uit een steekproef ter ondersteuning van de claim.
Hypothesetesten, ook wel significantietesten genoemd, zijn een methode voor het bevestigen van een claim of hypothese over een parameter in een populatie met behulp van gegevens die in een steekproef zijn gemeten. Met behulp van deze methode onderzoeken we verschillende theorieën door de mogelijkheid te bepalen dat, als de populatieparameterhypothese waar zou zijn geweest, een steekproefstatistiek zou zijn geselecteerd.
Het testen van hypothesen omvat het formuleren van twee hypothesen:
- Nulhypothese (H0)
- Alternatieve hypothese (H1)
Nulhypothese: Het is meestal een hypothese zonder verschil en wordt meestal aangeduid met H0. Volgens RA Fisher is de nulhypothese de hypothese die wordt getest op mogelijke verwerping onder de veronderstelling dat deze waar is (Ref Fundamentals of Mathematical Statistics).
Alternatieve hypothese: Elke hypothese die complementair is aan de nulhypothese wordt een alternatieve hypothese genoemd, meestal aangeduid met H1.
Het doel van het testen van hypothesen is het verwerpen of behouden van een nulhypothese om een statistisch significante relatie tussen twee variabelen vast te stellen (meestal één onafhankelijke en één afhankelijke variabele, dwz meestal is één de oorzaak en één het gevolg).
Hypothesetest opzetten
- Beschrijf de hypothese in woorden of maak een bewering.
- Definieer op basis van de claim nul- en alternatieve hypothesen.
- Identificeer het type hypothesetest dat geschikt is voor de bovenstaande bewering.
- Identificeer de teststatistieken die moeten worden gebruikt voor het testen van de geldigheid van de nulhypothese.
- Bepaal de criteria voor het verwerpen en behouden van de nulhypothese. Dit wordt significantiewaarde genoemd, traditioneel aangeduid met symbool α (alfa).
- Bereken de p-waarde, die de voorwaardelijke waarschijnlijkheid is van het waarnemen van de teststatistiekwaarde wanneer de nulhypothese waar is. Simpel gezegd is de p-waarde het bewijs ter ondersteuning van de nulhypothese.
Parametrische en niet-parametrische test
Niet-parametrische statistische tests zijn niet afhankelijk van aannames over de parameters van de populatieverdelingen waaruit de gegevens worden bemonsterd, terwijl parametrische statistische tests dat wel doen.
Parametrische tests
De meeste statistische tests worden uitgevoerd op basis van een reeks aannames als basis. De analyse kan misleidende of volledig valse conclusies opleveren wanneer bepaalde aannames worden geschonden.
Meestal zijn de aannames:
- Normaliteit: De steekproefverdeling van de te testen parameters volgt een normale (of op zijn minst symmetrische) verdeling.
- Homogeniteit van varianties: De variantie van de gegevens is hetzelfde voor verschillende groepen, tenzij we testen op populatiegemiddelden die uit twee verschillende populaties komen.
Enkele van de parametrische tests zijn:
- Z-test: Test op populatiegemiddelde, variantie of proportie wanneer de standaarddeviatie van de populatie bekend is.
- Student's t-toets: Test op populatiegemiddelde, variantie of proportie als de standaarddeviatie van de populatie niet bekend is.
- Gepaarde t-test: Wordt gebruikt om de gemiddelden van twee verwante groepen of omstandigheden te vergelijken.
- Variantieanalyse (ANOVA): Wordt gebruikt om gemiddelden van drie of meer onafhankelijke groepen te vergelijken.
- Regressie analyse: Wordt gebruikt om de relatie tussen een of meer onafhankelijke variabelen en een afhankelijke variabele te beoordelen.
- Analyse van covariantie (ANCOVA): Breidt ANOVA uit door extra covariaten in de analyse op te nemen.
- Multivariate variantieanalyse (MANOVA): Breidt ANOVA uit om verschillen in meerdere afhankelijke variabelen tussen groepen te beoordelen.
Laten we nu eens dieper ingaan op de niet-parametrische test.
Niet-parametrische test
Voor het eerst gebruikte Wolfowitz de term ‘niet-parametrische’ in 1942. Om het idee van niet-parametrische statistiek te begrijpen, moet men eerst een basiskennis hebben van parametrische statistiek, die we zojuist hebben besproken. A parametrische test vereist een monster dat een specifieke verdeling volgt (meestal normaal). Bovendien zijn niet-parametrische tests onafhankelijk van parametrische aannames zoals normaliteit.
Niet-parametrische tests (ook wel distributievrije tests genoemd, omdat ze geen aannames hebben over de verdeling van de populatie). Niet-parametrische tests impliceren dat de tests niet gebaseerd zijn op de aannames dat de gegevens afkomstig zijn uit a kansverdeling gedefinieerd door parameters zoals gemiddelde, proportie en standaarddeviatie.
Niet-parametrische tests worden gebruikt wanneer:
- De test gaat niet over de populatieparameter zoals gemiddelde of proportie.
- De methode vereist geen aannames over de populatieverdeling (zoals de populatie een normale verdeling volgt).
Soorten niet-parametrische tests
Laten we nu het concept en de procedure bespreken voor het uitvoeren van de Chi-Square-test, Mann-Whitney-test, Wilcoxon Signed Rank-test en Kruskal-Wallis-tests:
Chikwadraattoets
Om te bepalen of het verband tussen twee kwalitatieve variabelen statistisch significant is, moet men een significantietest uitvoeren, de Chi-kwadraattest.
Er zijn twee hoofdtypen Chi-kwadraattoetsen:
Chi-kwadraat Goodness-of-Fit
Gebruik de goodness-of-fit test om te beslissen of een populatie met een onbekende verdeling “past” in een bekende verdeling. In dit geval zal er sprake zijn van een enkele kwalitatieve onderzoeksvraag of een enkele uitkomst van een experiment uit een enkele populatie. Goodness-of-Fit wordt doorgaans gebruikt om te zien of de populatie uniform is (alle uitkomsten komen met gelijke frequentie voor), de populatie normaal is of dat de populatie hetzelfde is als een andere populatie met een bekende verdeling. De nul- en alternatieve hypothesen zijn:
- H0: De populatie past in de gegeven verdeling.
- Ha: De populatie past niet in de gegeven verdeling.
Laten we dit begrijpen met een voorbeeld
| Dag | maandag | dinsdag | woensdag | donderdag | vrijdag | zaterdag | zondag |
| Aantal storingen | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
De tabel toont het aantal uitsplitsingen in een factor. In dit voorbeeld is er slechts één variabele en moeten we bepalen of de waargenomen verdeling (weergegeven in de tabel) past bij de verwachte verdeling of niet.
Hiervoor zullen de nulhypothese en de alternatieve hypothese als volgt worden geformuleerd:
- H0:De storingen zijn gelijkmatig verdeeld.
- Ha: Uitsplitsingen zijn niet uniform verdeeld.
En de vrijheidsgraad zal n-1 zijn (in dit geval n=7, dus df = 7-1=6)
Expected value will be= (14+22+16+18+12+19+11)/7=16
| Dag | maandag | dinsdag | woensdag | donderdag | vrijdag | zaterdag | zondag |
| Aantal storingen (waargenomen) | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
| verwacht | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| (waargenomen-verwacht) | -2 | 6 | 0 | 2 | -4 | 3 | -5 |
| (waargenomen-verwacht)^2 | 4 | 36 | 0 | 4 | 16 | 9 | 25 |
Met deze formule Bereken Chi-kwadraat
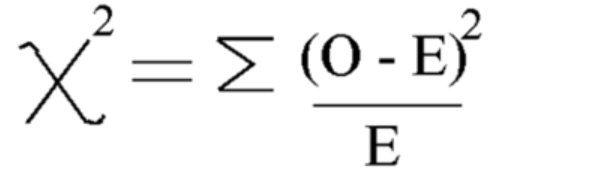
Chi-kwadraat = 5.875
En de vrijheidsgraad is = n-1=7-1=6
Laten we nu eens kijken naar de kritische waarde van chi vierkante verdeeltafel op een significantieniveau van 5%
De kritische waarde is dus 12.592
Omdat de berekende Chi-kwadraatwaarde kleiner is dan de kritische waarde, aanvaarden we de nulhypothese en kunnen we concluderen dat de uitsplitsingen uniform verdeeld zijn.
Chi-kwadraat-onafhankelijkheid van test
Gebruik de onafhankelijkheidstest om te beslissen of twee variabelen (factoren) onafhankelijk of afhankelijk zijn, dwz of deze twee variabelen al dan niet een significante associatierelatie hebben. In dit geval zullen er twee kwalitatieve enquêtevragen of experimenten zijn en zal er een kruistabel worden opgesteld. Het doel is om te zien of de twee variabelen geen verband houden (onafhankelijk) of gerelateerd (afhankelijk). De nul- en alternatieve hypothesen zijn:
- H0: De twee variabelen (factoren) zijn onafhankelijk.
- Ha: De twee variabelen (factoren) zijn afhankelijk.
Laten we een voorbeeld nemen
Voorbeeld waarin we willen onderzoeken of geslacht en voorkeurskleur van shirt onafhankelijk waren. Dit betekent dat we willen weten of het geslacht van een persoon de kleurkeuze beïnvloedt. We hebben een onderzoek uitgevoerd en de gegevens in de tabel geordend.
Deze tabel is waargenomen waarden:
| Zwart | Wit | Rood | Blauw | |
| Mannelijk frezen | 48 | 12 | 33 | 57 |
| Female | 34 | 46 | 42 | 26 |
Formuleer nu eerst nul- en alternatieve hypothesen
- H0: Geslacht en voorkeurskleur van het shirt zijn onafhankelijk
- Ha: Geslacht en voorkeurskleur van het shirt zijn niet onafhankelijk
Voor het berekenen van Chi-kwadraat-teststatistieken moeten we de verwachte waarde berekenen. Voeg dus alle rijen en kolommen en de totale totalen toe:
| Zwart | Wit | Rood | Blauw | Totaal | |
| Mannelijk frezen | 48 | 12 | 33 | 57 | 150 |
| Female | 34 | 46 | 42 | 26 | 148 |
| Totaal | 82 | 58 | 75 | 83 | 298 |
Hierna kunnen we voor elke invoer de verwachte waardetabel uit de bovenstaande tabel berekenen met behulp van deze formule = (rijtotaal * kolomtotaal)/totaaltotaal
Verwachte waarde Tabel:
| Zwart | Wit | Rood | Blauw | |
| Mannelijk frezen | 41.3 | 29.2 | 37.8 | 41.8 |
| Female | 40.7 | 28.8 | 37.2 | 41.2 |
Bereken nu de Chi-kwadraatwaarde met behulp van de formule voor chi-kwadraattest:
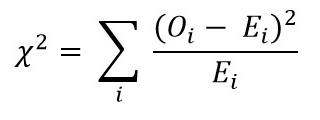
- Oi = Waargenomen waarde
- Ei = Verwachte waarde
De waarde die we krijgen is: Χ2 = 34.9572
Bereken de vrijheidsgraad
DF=(aantal rij-1)*(aantal kolom-1)
Zoek en vergelijk nu de kritische waarde met de chikwadraattoets statistische waarde:
Hiervoor kunt u de vrijheidsgraad en het significantieniveau (alfa) opzoeken in de chi-kwadraat verdeeltafel
Bij alfa = 0.050 krijgen we een kritische waarde = 7.815
Sinds chikwadraat > kritische waarde
Daarom verwerpen we de nulhypothese en kunnen we concluderen dat geslacht en voorkeurskleur van het shirt niet onafhankelijk zijn.
Implementatie van Chi-Square
Laten we nu de implementatie van Chi-Square bekijken aan de hand van een voorbeeld uit de praktijk in Python:
- H0: Geslacht en voorkeurskleur van het shirt zijn onafhankelijk
- Ha: Geslacht en voorkeurskleur van het shirt zijn niet onafhankelijk
Gegevensset maken:
import pandas as pd
from scipy.stats import chi2_contingency
from scipy.stats import chi2
# Given dataset
df_dict = {
'Black': [48, 34],
'White': [12, 46],
'Red': [33, 42],
'Blue': [57, 26]
}
dataset_table = pd.DataFrame(df_dict, index=['Male', 'Female'])
print("Dataset Table:")
print(dataset_table)
print()
# Observed Values
Observed_Values = dataset_table.values
print("Observed Values:")
print(Observed_Values)
print()
# Perform chi-square test
val = chi2_contingency(dataset_table)
Expected_Values = val[3]
print("Expected Values:")
print(Expected_Values)
print()
# Degree of Freedom
no_of_rows = len(dataset_table.iloc[0:2, 0])
no_of_columns = 4
ddof = (no_of_rows - 1) * (no_of_columns - 1)
print("Degree of Freedom:", ddof)
print()
# Chi-square statistic
chi_square = sum([(o - e) ** 2. / e for o, e in zip(Observed_Values, Expected_Values)])
chi_square_statistic = chi_square[0] + chi_square[1]
print("Chi-square statistic:", chi_square_statistic)
print()
# Critical value
alpha = 0.05
critical_value = chi2.ppf(q=1-alpha, df=ddof)
print('Critical value:', critical_value)
print()
# p-value
p_value = 1 - chi2.cdf(x=chi_square_statistic, df=ddof)
print('p-value:', p_value)
print()
# Significance level
print('Significance level:', alpha)
print('p-value:', p_value)
print('Degree of Freedom:', ddof)
print()
# Hypothesis testing
if chi_square_statistic >= critical_value:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
print()
if p_value <= alpha:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
Output:
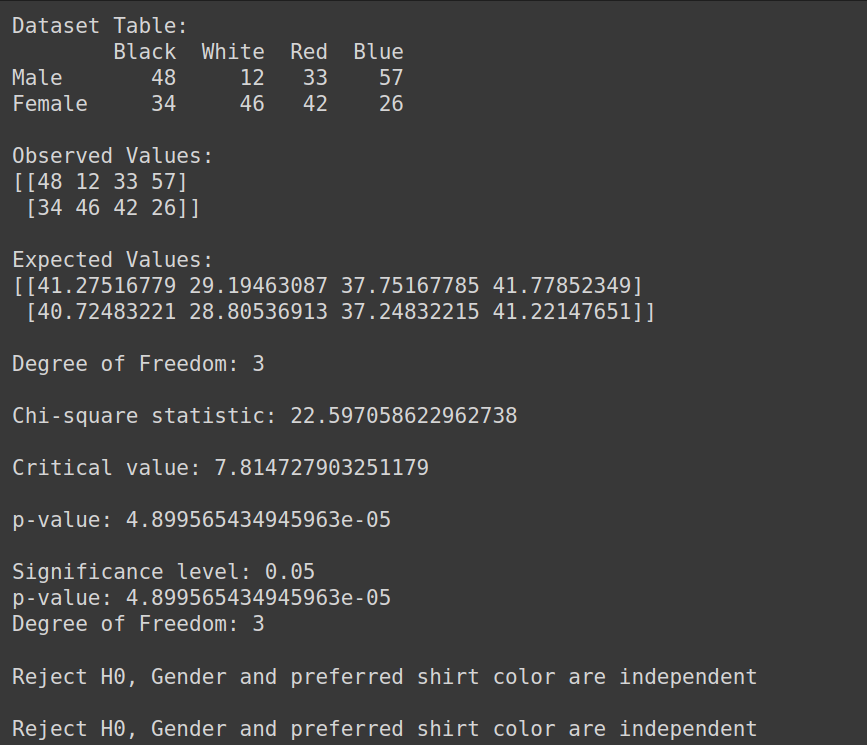
Mann-Whitney U-test
De Mann-Whitney U-test dient als het niet-parametrische alternatief voor de onafhankelijke steekproef-t-test. Het vergelijkt twee steekproefgemiddelden uit dezelfde populatie en bepaalt of ze gelijk zijn. Deze test wordt doorgaans gebruikt voor ordinale gegevens of wanneer niet aan de aannames van de t-test wordt voldaan.
De Mann-Whitney U-test rangschikt alle waarden van beide groepen samen en telt vervolgens de waarden voor elke groep bij elkaar op. Het berekent de teststatistiek, U, op basis van deze rangen. De U-statistiek wordt vergeleken met een kritische waarde uit een tabel of berekend met behulp van een benadering. Als de U-statistiek kleiner is dan de kritische waarde, wordt de nulhypothese verworpen.
Dit verschilt van parametrische tests zoals de t-test, waarbij gemiddelden worden vergeleken en een normale verdeling wordt aangenomen. De Mann-Whitney U-test vergelijkt in plaats daarvan rangen en vereist niet de aanname van een normale verdeling.
Het begrijpen van de Mann-Whitney U-test kan moeilijk zijn omdat de resultaten worden gepresenteerd in groepsrangverschillen in plaats van in groepsgemiddelden.
Formule voor Mann-Whitney-test:
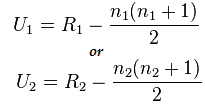
U=min(U1,U2)
Hier
- U= Mann-Whitney U-test
- n1= steekproefomvang één
- n2= steekproefomvang twee
- R1= Rang van steekproefomvang één
- R2= Rang van steekproefomvang 2
Laten we dit dus begrijpen met een kort voorbeeld:
Stel dat we de effectiviteit van twee verschillende behandelmethoden (methode A en methode B) willen vergelijken bij het verbeteren van de gezondheid van patiënten. Wij beschikken over de volgende gegevens:
- Methode A: 3,4,2,6,2,5
- Methode B: 9,7,5,10,6,8
Hier kunnen we zien dat de gegevens niet normaal verdeeld zijn en dat de steekproefomvang klein is.
Implementatie van Mann-Whitney U-test
Laten we nu de Mann-Whitney U-test uitvoeren:
Maar laten we eerst de nul- en alternatieve hypothese formuleren
- H0: Er is geen verschil tussen de rangorde van elke behandeling
- Ha: Er is een verschil tussen de rangorde van elke behandeling
Combineer alle behandelingen: 3,4,2,6,2,5,9,7,5,10,6,8
Gesorteerde gegevens: 2,2,3,4,5,5,6,6,7,8,9,10
Rang van gesorteerde gegevens: 1,2,3,4,5,6,7,8,9,10,11,12
- De gegevens afzonderlijk rangschikken:
- Method A: 3(3),4(4),2(1.5),6(7.5),2(1.5),5(5.5)
- Method B: 9(11),7(9),5(5.5),10(12),6(1.5),8(10)
- Som van rang berekenen):
- R1: 3+4+1.5+7.5+1.5+5.5=23
- R2: 11+9+5.5+12+1.5+10=55
Bereken nu de statistische waarde met behulp van deze formule:
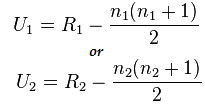
Hier geldt n1=6 en n2=6
En de waarde na berekening voor U1=2 en voor U2= 34
U-statistiek berekenen:
Us= min(U1,U2)= min(2,34)= 2
Van Mann-Whitney-tafel we kunnen de kritische waarde vinden
In dit geval is de kritische waarde 5
Omdat Uc = 5, wat groter is dan Wij op een significantieniveau van 5%, verwerpen we dus H0
Daarom kunnen we concluderen dat er een verschil is tussen de rangorde van elke behandeling.
Implementatie met python
from scipy.stats import mannwhitneyu, norm
import numpy as np
TreatmentA = np.array([3,4,2,6,2,5])
TreatmentB = np.array([9,7,5,10,6,8])
# Perform Mann-Whitney U test
U_statistic, p_value = mannwhitneyu(TreatmentA, TreatmentB)
# Print the result
print(f'The U-statistic is {U_statistic:.2f} and the p-value is {p_value:.4f}')
if p_value < 0.05:
print("Reject Null Hypothesis: There is a significant difference between the Rank of each treatment.")
else:
print("Fail to Reject Null Hypothesis: Fail to Reject Null Hypothesis: There is no enough evidence to conclude that there is difference between the Rank of each treatment")Output:

Kruskal-Wallis-test
Kruskal –Wallis Test wordt gebruikt met meerdere groepen. Het is het niet-parametrische en een waardevol alternatief voor een eenrichtings-ANOVA-test wanneer de aannames over normaliteit en gelijkheid van variantie worden geschonden. De Kruskal-Wallis-test vergelijkt de medianen van meer dan twee onafhankelijke groepen.
Het test de nulhypothese wanneer k onafhankelijke steekproeven (k>=3) worden getrokken uit een populatie met identieke verdelingen, zonder dat de voorwaarde van normaliteit voor de populaties vereist is.
Veronderstellingen:
Zorg ervoor dat er minimaal drie onafhankelijk getrokken willekeurige steekproeven zijn. Elk monster heeft minimaal 5 waarnemingen, n>=5
Beschouw een voorbeeld waarin we willen bepalen of de studietechniek die door drie groepen studenten wordt gebruikt, hun examenscores beïnvloedt. We kunnen de Kruskal-Wallis Test gebruiken om de gegevens te analyseren en te beoordelen of er statistisch significante verschillen zijn in examenscores tussen de groepen.
Formuleer de nulhypothese hiervoor als:
- H0: Er is geen verschil in examenscores tussen de drie groepen studenten.
- Ha: Er is een verschil in examenscores tussen de drie groepen studenten.
Wilcoxon ondertekende rangtest
Wilcoxon Signed Rank Test (ook bekend als Wilcoxon Matched Pair Test) is de niet-parametrische versie van de afhankelijke steekproef t-test of gepaarde steekproef t-test. Tekentest is het andere niet-parametrische alternatief voor de gepaarde steekproef-t-test. Het wordt gebruikt wanneer de relevante variabelen dichotoom van aard zijn (zoals mannelijk en vrouwelijk, ja en nee). Wilcoxon Signed Rank Test is ook een niet-parametrische versie voor één steekproef-t-test. De Wilcoxon Signed Rank Test vergelijkt de mediaan van de groepen in twee situaties (gepaarde steekproeven) of vergelijkt de mediaan van de groep met de veronderstelde mediaan (één steekproef).
Laten we dit met een voorbeeld begrijpen. Stel dat we gegevens hebben over de dagelijkse sigarettenconsumptie van rokers voor en na deelname aan een programma van 8 weken en we willen bepalen of er een significant verschil is in de dagelijkse sigarettenconsumptie voor en na het programma. Dan zullen we dat doen. gebruik deze proef
De hypotheseformulering hiervoor zal zijn
- H0: Er is geen verschil in de dagelijkse sigarettenconsumptie voor en na het programma.
- Ha: Er is een verschil in de dagelijkse sigarettenconsumptie voor en na het programma
Test voor normaliteit
Laten we nu de normaliteitstests bespreken:
Shapiro Wilk-test
De Shapiro-Wilk-test beoordeelt of een bepaalde steekproef van gegevens afkomstig is van een normaal verdeelde populatie. Het is een van de meest gebruikte tests om de normaliteit te controleren. De test is vooral nuttig als het om relatief kleine steekproeven gaat.
In de Shapiro-Wilk-test:
- Nulhypothese: De steekproefgegevens zijn afkomstig van een populatie die een normale verdeling volgt.
- Alternatieve hypothese: De steekproefgegevens zijn niet afkomstig van een populatie die een normale verdeling volgt.
De teststatistiek gegenereerd door de Shapiro-Wilk-test meet de discrepantie tussen de waargenomen gegevens en de verwachte gegevens onder de aanname van normaliteit. Als de p-waarde geassocieerd met de teststatistiek kleiner is dan een gekozen significantieniveau (bijvoorbeeld 0.05), verwerpen we de nulhypothese, wat aangeeft dat de gegevens niet normaal verdeeld zijn. Als de p-waarde groter is dan het significantieniveau, slagen we er niet in de nulhypothese te verwerpen, wat suggereert dat de gegevens een normale verdeling kunnen volgen.
Laten we eerst een dataset maken voor deze test. U kunt elke dataset naar keuze gebruiken:
import pandas as pd
# Create the dictionary with the provided data
data = {
'population': [6.1101, 5.5277, 8.5186, 7.0032, 5.8598],
'profit': [17.5920, 9.1302, 13.6620, 11.8540, 6.8233]
}
# Create the DataFrame
df = pd.DataFrame(data)
response_var=df['profit']
Here, a sample for running Shapiro -Wilk test on python:
from scipy.stats import shapiro
stat, p_val = shapiro(response_var)
print(f'Shapiro-Wilk Test: Statistic={stat} p-value={p_val}')
if p_val > alpha:
print('Data looks normal (fail to reject H0)')
else:
print('Data looks normal (fail to reject H0)')Output:

Deze test is het meest geschikt voor relatief kleine steekproeven (n=< 50-2000), omdat deze minder betrouwbaar wordt bij grotere steekproeven.
Anderson-Darling
Het beoordeelt of een bepaalde steekproef van gegevens afkomstig is uit een specifieke verdeling, zoals de normale verdeling. Het is vergelijkbaar met de Shapiro-Wilk-test, maar is gevoeliger, vooral voor kleinere steekproeven.
Het is geschikt voor verschillende verdelingen, inclusief de normale verdeling, voor gevallen waarin de parameters van de verdeling onbekend zijn.
Hier, Python-code voor de implementatie ervan:
from scipy.stats import anderson
response_var = data['profit']
alpha = 0.05
# Anderson-Darling Test
result = anderson(response_var)
print(f'Anderson statistics: {result.statistic:.3f}')
if result.statistic > result.critical_values[-1]:
p_value = 0.0 # The p-value is essentially 0 if the statistic exceeds the largest critical value
else:
p_value = result.significance_level[result.statistic < result.critical_values][-1]
print("P-value:", p_value)
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")Output:

Jarque-Bera-test
De Jarque-Bera-test beoordeelt of een bepaalde steekproef van gegevens afkomstig is van een normaal verdeelde populatie. Het is gebaseerd op de scheefheid en kurtosis van de gegevens.
Hier is de implementatie van Jarque-Bera Test in Python met voorbeeldgegevens:
from scipy.stats import jarque_bera
# Performing Jarque-Bera test
test_statistic, p_value = jarque_bera(response_var)
print("Jarque-Bera Test Statistic:", test_statistic)
print("P-value:", p_value)
# Interpreting results
alpha = 0.05
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")Output:

| Categorie | Parametrische statistische technieken | Niet-parametrisch Statistischtechnieken |
| correlatie | Pearson productmomentcorrelatiecoëfficiënt (r) | Spearman rangschikkingscoëfficiëntcorrelatie (Rho), Kendall's Tau |
| Twee groepen, onafhankelijke maatregelen | Onafhankelijke t-test | Mann-Whitney U-test |
| Meer dan twee groepen, onafhankelijke maatregelen | Eenrichtings ANOVA | Kruskal-Wallis enkele reis-ANOVA |
| Twee groepen, herhaalde maatregelen | Gepaarde t-test | Wilcoxon matched pair ondertekende rangtest |
| Meer dan twee groepen, herhaalde maatregelen | ANOVA met herhaalde metingen in één richting | Friedman's tweerichtingsanalyse van variantie |
Conclusie
Hypothese testen is essentieel voor het evalueren van claims over populatieparameters met behulp van steekproefgegevens. Parametrische tests zijn gebaseerd op specifieke aannames en zijn geschikt voor interval- of ratiogegevens, terwijl niet-parametrische tests flexibeler zijn en toepasbaar op nominale of ordinale gegevens zonder strikte verdelingsaannames. Tests zoals Shapiro-Wilk en Anderson-Darling beoordelen de normaliteit, terwijl Chi-square en Jarque-Bera de goedheid van de pasvorm beoordelen. Het begrijpen van de verschillen tussen parametrische en niet-parametrische tests is cruciaal voor het selecteren van de juiste statistische benadering. Over het geheel genomen biedt het testen van hypothesen een systematisch raamwerk voor het nemen van datagestuurde beslissingen en het trekken van betrouwbare conclusies uit empirisch bewijs.
Klaar om geavanceerde statistische analyse onder de knie te krijgen? Schrijf u vandaag nog in voor onze BlackBelt Data-analysecursus! Verkrijg expertise in het testen van hypothesen, parametrische en niet-parametrische tests, Python-implementatie en meer. Verbeter uw statistische vaardigheden en blink uit in datagestuurde besluitvorming. Sluit je nu aan!
Veelgestelde Vragen / FAQ
A. Parametrische tests maken aannames over de populatieverdeling en parameters, zoals normaliteit en homogeniteit van variantie, terwijl niet-parametrische tests niet op deze aannames vertrouwen. Parametrische tests hebben meer kracht als aan aannames wordt voldaan, terwijl niet-parametrische tests robuuster zijn en toepasbaar in een breder scala aan situaties, ook wanneer gegevens scheef zijn of niet normaal verdeeld zijn.
A. De chikwadraattoets wordt gebruikt om te bepalen of er een significant verband bestaat tussen twee categorische variabelen. Het analyseert gewoonlijk categorische gegevens en test hypothesen over de onafhankelijkheid van variabelen in kruistabellen.
A. De Mann-Whitney U-test vergelijkt twee onafhankelijke groepen wanneer de afhankelijke variabele ordinaal of niet normaal verdeeld is. Er wordt beoordeeld of er een significant verschil bestaat tussen de medianen van de twee groepen.
A. De Shapiro-Wilk-test beoordeelt of een steekproef afkomstig is uit een normaal verdeelde populatie. Het test de nulhypothese dat de gegevens een normale verdeling volgen. Als de p-waarde kleiner is dan het gekozen significantieniveau (bijvoorbeeld 0.05), verwerpen we de nulhypothese en concluderen we dat de gegevens niet normaal verdeeld zijn.
- Door SEO aangedreven content en PR-distributie. Word vandaag nog versterkt.
- PlatoData.Network Verticale generatieve AI. Versterk jezelf. Toegang hier.
- PlatoAiStream. Web3-intelligentie. Kennis versterkt. Toegang hier.
- PlatoESG. carbon, CleanTech, Energie, Milieu, Zonne, Afvalbeheer. Toegang hier.
- Plato Gezondheid. Intelligentie op het gebied van biotech en klinische proeven. Toegang hier.
- Bron: https://www.analyticsvidhya.com/blog/2024/04/a-comprehensive-guide-on-non-parametric-tests/



