Vitalik Buterin via de Vitalik Buterin-blog

Dit is een spiegel van het bericht op https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627

Triggerwaarschuwing: wiskunde.

Een van de belangrijkste cryptografische primitieven achter verschillende constructies, waaronder deterministische drempelsignaturen, zk-SNARK's en andere eenvoudigere vormen van nulkennisbewijzen, is de elliptische curve-paring. Elliptische curve-paren (of “bilineaire kaarten”) zijn een recente toevoeging aan een 30-jarige geschiedenis van het gebruik van elliptische curven voor cryptografische toepassingen, waaronder encryptie en digitale handtekeningen; koppelingen introduceren een vorm van “gecodeerde vermenigvuldiging”, waardoor de mogelijkheden van op elliptische curven gebaseerde protocollen aanzienlijk worden uitgebreid. Het doel van dit artikel is om gedetailleerd in te gaan op elliptische curveparen en een algemeen overzicht uit te leggen van hoe ze werken.

Er wordt niet van je verwacht dat je alles hier begrijpt de eerste keer dat je het leest, of zelfs de tiende keer; dit spul is echt moeilijk. Maar hopelijk geeft dit artikel je op zijn minst een beetje een idee van wat er onder de motorkap gebeurt.

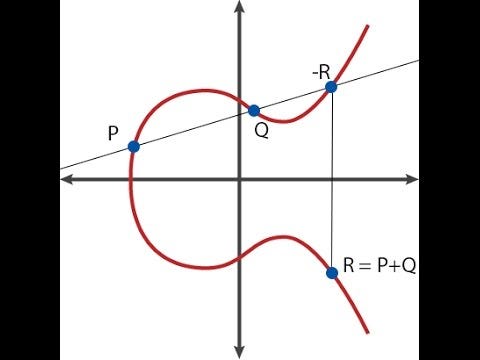
Elliptische curven zelf zijn een niet-triviaal onderwerp om te begrijpen, en dit artikel gaat er over het algemeen van uit dat je weet hoe ze werken; Als je dat niet doet, raad ik dit artikel hier aan als inleiding: https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/. Kort samengevat omvat cryptografie met elliptische curven wiskundige objecten die “punten” worden genoemd (dit zijn letterlijk tweedimensionale punten met (�,�) coördinaten), met speciale formules voor het optellen en aftrekken ervan (dwz voor het berekenen van de coördinaten van �= �+�), en je kunt een punt ook vermenigvuldigen met een geheel getal (dat wil zeggen �⋅�=�+�+…+�, hoewel er een veel snellere manier is om het te berekenen als � groot is).

Zo ziet het optellen van punten er grafisch uit.

Er bestaat een speciaal punt dat het “punt op oneindig” (�) wordt genoemd, het equivalent van nul in de rekenkunde; het is altijd zo dat �+�=�. Ook heeft een curve een “bestellen“; er bestaat een getal � zodat �⋅�=� voor elke � (en natuurlijk �⋅(�+1)=�,�⋅(7⋅�+5)=�⋅5, enzovoort). Er is ook een algemeen overeengekomen “generatorpunt” �, waarvan wordt aangenomen dat het in zekere zin het getal 1 vertegenwoordigt. Theoretisch kan elk punt op een curve (behalve �) � zijn; het enige dat telt is dat � gestandaardiseerd is.

Paren gaan nog een stap verder in die zin dat u hiermee bepaalde soorten ingewikkeldere vergelijkingen op elliptische curvepunten kunt controleren — als u bijvoorbeeld �=�⋅�,�=�⋅� en �=�⋅� kunt controleren of niet �⋅�=�, met alleen �,� en � als invoer. Dit lijkt misschien alsof de fundamentele veiligheidsgaranties van elliptische krommen worden geschonden, omdat informatie over � lekt door alleen maar P te kennen, maar het blijkt dat de lekkage zeer beperkt is — met name de beslissingsprobleem van Diffie Hellman is eenvoudig, maar het computationele Diffie Hellman-probleem (het kennen van � en � in het bovenstaande voorbeeld, computergebruik �=�⋅�⋅�) en de discreet logaritme probleem (het herstellen van � uit �) blijven computationeel onhaalbaar (althans, als ze dat al eerder waren).

Een derde manier om te kijken naar wat koppelingen doen, en een die misschien wel het meest verhelderend is voor de meeste gebruiksscenario’s waar we het over hebben, is door elliptische curvepunten te beschouwen als in één richting gecodeerde getallen (dat wil zeggen, ���� ���(�)=�⋅�=�), terwijl je met traditionele elliptische curve-berekeningen dit kunt controleren lineair beperkingen op de getallen (bijv. als �=�⋅�,�=�⋅� en �=�⋅�, controleren of 5⋅�+7⋅�=11⋅� is werkelijk als je dat controleert 5⋅�+7⋅�=11⋅�), kun je met paren controleren vierkant beperkingen (bijv. controleren of �(�,�)⋅�(�,�⋅5)=1 is werkelijk controleer of �⋅�+5=0). En naar kwadratisch gaan is voldoende om ons te laten werken met deterministische drempelsignaturen, kwadratische rekenprogramma's en al die andere goede dingen.

Wat is nu deze grappige �(�,�) operator die we hierboven hebben geïntroduceerd? Dit is de koppeling. Wiskundigen noemen het ook wel eens een bilineaire kaart; het woord ‘bilineair’ betekent hier feitelijk dat het aan de beperkingen voldoet:

�(�,�+�)=�(�,�)⋅�(�,�)

�(�+�,�)=�(�,�)⋅�(�,�)

Merk op dat + en ⋅ willekeurige operatoren kunnen zijn; als je mooie nieuwe soorten wiskundige objecten maakt, maakt het abstracte algebra niet uit hoe + en ⋅ zijn gedefinieerd, zolang ze op de gebruikelijke manieren consistent zijn, bijv. �+�=�+�,(�⋅�)⋅�=�⋅(�⋅�) en (�⋅�)+(�⋅�)=(�+�)⋅�.

Als �, �, � en � eenvoudig waren nummers, dan is het maken van een eenvoudige koppeling eenvoudig: we kunnen �(�,�)=2�� doen. Dan kunnen we zien:

�(3,4+5)=23⋅9=227

�(3,4)⋅�(3,5)=23⋅4⋅23⋅5=212⋅215=227

Het is bilineair!

Dergelijke eenvoudige combinaties zijn echter niet geschikt voor cryptografie, omdat de objecten waaraan ze werken eenvoudige gehele getallen zijn en te gemakkelijk te analyseren zijn; gehele getallen maken het gemakkelijk om te delen, logaritmen te berekenen en diverse andere berekeningen uit te voeren; eenvoudige gehele getallen hebben geen concept van een “publieke sleutel” of een “eenrichtingsfunctie”. Bovendien kunt u met de hierboven beschreven koppeling achteruit gaan – als u � kent, en als u �(�,� kent), kunt u eenvoudigweg een deling en een logaritme berekenen om � te bepalen. We willen wiskundige objecten die zo dicht mogelijk bij ‘zwarte dozen’ liggen, waar je kunt optellen, aftrekken, vermenigvuldigen en delen, maar doe niets anders. Dit is waar elliptische curven en elliptische curve-paren binnenkomen.

Het blijkt dat het mogelijk is om een ​​bilineaire kaart te maken over elliptische curvepunten – dat wil zeggen: bedenk een functie �(�,�) waarbij de inputs � en � elliptische curvepunten zijn, en waarbij de output een zogenaamde (��)12 element (tenminste in het specifieke geval dat we hier zullen behandelen; de details verschillen afhankelijk van de details van de curve, hierover later meer), maar de wiskunde hierachter is behoorlijk complex.

Laten we eerst de hoofdvelden en extensievelden bespreken. De mooie elliptische curve in de afbeelding eerder in dit bericht ziet er alleen zo uit als je aanneemt dat de curvevergelijking is gedefinieerd met behulp van reguliere reële getallen. Als we echter in de cryptografie daadwerkelijk gewone reële getallen gebruiken, kun je logaritmen gebruiken om ‘achteruit te gaan’, en alles gaat kapot; bovendien kan de hoeveelheid ruimte die nodig is om de getallen daadwerkelijk op te slaan en weer te geven willekeurig groeien. Daarom gebruiken we in plaats daarvan getallen in a prime veld.

Een priemveld bestaat uit de reeks getallen 0,1,2…�−1, waarbij � een priemgetal is, en de verschillende bewerkingen worden als volgt gedefinieerd:

�+�:(�+�) % �

�⋅�:(�⋅�) % �

�−�:(�−�) % �

�/�:(�⋅��−2) % �

In principe wordt alle wiskunde modulo � gedaan (zie hier voor een inleiding tot modulaire wiskunde). Verdeling is een speciaal geval; normaal gesproken is 32 geen geheel getal, en hier willen we alleen met gehele getallen te maken hebben, dus proberen we in plaats daarvan het getal � te vinden zodat �⋅2=3, waarbij ⋅ uiteraard verwijst naar modulaire vermenigvuldiging zoals hierboven gedefinieerd. Dankzij De kleine stelling van Fermat, de hierboven getoonde machtsverheffingstruc doet het werk, maar er is ook een snellere manier om het te doen, met behulp van de Uitgebreide Euclidische Algoritme. Stel �=7; hier zijn een paar voorbeelden:

2+3=5 % 7=5

4+6=10 % 7=3

2−5=−3 % 7=4

6⋅3=18 % 7=4

3/2=(3⋅25) % 7=5

5⋅2=10 % 7=3

Als je met dit soort wiskunde speelt, zul je merken dat het volkomen consistent is en aan alle gebruikelijke regels voldoet. De laatste twee voorbeelden hierboven laten zien hoe (�/�)⋅�=�; je kunt ook zien dat (�+�)+�=�+(�+�),(�+�)⋅�=�⋅�+�⋅�, en alle andere algebraïsche identiteiten op de middelbare school die je kent en waar je van houdt, blijven bestaan ook waar te houden. In werkelijkheid worden bij elliptische krommen de punten en vergelijkingen gewoonlijk in priemvelden berekend.

Laten we het nu hebben extensie velden. Waarschijnlijk heb je al eerder een extensieveld gezien; het meest voorkomende voorbeeld dat je tegenkomt in wiskundeboeken is het veld van complexe getallen, waarbij het veld van reële getallen wordt “uitgebreid” met het extra element −1=�. In principe werken uitbreidingsvelden door een bestaand veld te nemen, vervolgens een nieuw element te ‘uitvinden’ en de relatie tussen dat element en bestaande elementen te definiëren (in dit geval �2+1=0), waarbij ervoor wordt gezorgd dat deze vergelijking niet opgaat. voor elk getal dat zich in het oorspronkelijke veld bevindt, en kijkend naar de verzameling van alle lineaire combinaties van elementen van het oorspronkelijke veld en het nieuwe element dat u zojuist hebt gemaakt.

We kunnen ook uitbreidingen van topvelden doen; We kunnen bijvoorbeeld het priemveld mod7 dat we hierboven hebben beschreven uitbreiden met �, en dan kunnen we het volgende doen:

(2+3�)+(4+2�)=6+5�

(5+2�)+3=1+2�

(6+2�)⋅2=5+4�

4�⋅(2+�)=3+�

Dat laatste resultaat is misschien een beetje moeilijk te achterhalen; wat daar gebeurde was dat we het product eerst ontleden in 4�⋅2+4�⋅�, wat 8�−4 oplevert, en omdat we met mod7-wiskunde werken, wordt dat dan �+3. Om te verdelen doen we:

�/�:(�⋅�(�2−2)) % �

Merk op dat de exponent voor de kleine stelling van Fermat nu �2 is in plaats van �, maar nogmaals, als we efficiënter willen zijn, kunnen we in plaats daarvan ook het Uitgebreide Euclidische Algoritme uitbreiden om de klus te klaren. Merk op dat ��2−1=1 voor elke � in dit veld, dus noemen we �2−1 de “volgorde van de multiplicatieve groep in het veld”.

Met reële cijfers is de Fundamentele stelling van de algebra zorgt ervoor dat de kwadratische uitbreiding die we de complexe getallen noemen ‘volledig’ is – je kunt deze niet verder uitbreiden, omdat je voor elke wiskundige relatie (althans elke wiskundige relatie gedefinieerd door een algebraïsche formule) die je kunt bedenken tussen een nieuw element � en de bestaande complexe getallen, is het mogelijk om minstens één complex getal te bedenken dat al aan die relatie voldoet. Met priemvelden hebben we dit probleem echter niet, en dus kunnen we verder gaan en kubieke uitbreidingen maken (waarbij de wiskundige relatie tussen een nieuw element � en bestaande veldelementen een kubieke vergelijking is, dus 1,� en �2 zijn allemaal lineair onafhankelijk van elkaar), uitbreidingen van hogere orde, uitbreidingen van uitbreidingen, enz. En het zijn dit soort supercharged modulaire complexe getallen waarop elliptische curve-paren zijn gebouwd.

Voor degenen die geïnteresseerd zijn in het zien van de exacte wiskunde die betrokken is bij het uitschrijven van al deze bewerkingen in code, zijn hier prime-velden en veldextensies geïmplementeerd: https://github.com/ethereum/py_pairing/blob/master/py_ecc/bn128/bn128_field_elements.py

Nu verder met elliptische curve-paren. Een elliptische curve-koppeling (of beter gezegd, de specifieke vorm van koppeling die we hier zullen onderzoeken; er zijn ook andere soorten koppelingen, hoewel hun logica redelijk gelijkaardig is) is een kaart �2×�1→��, waarbij:

• �1 is een elliptische curve, waarbij punten voldoen aan een vergelijking van de vorm �2=�3+�, en waarbij beide coördinaten elementen zijn van �� (dat wil zeggen: het zijn eenvoudige getallen, behalve dat rekenkunde allemaal wordt gedaan modulo een priemgetal)
• �2 is een elliptische curve, waarbij punten aan dezelfde vergelijking voldoen als �1, behalve waar de coördinaten elementen zijn van (��)12 (dat wil zeggen: het zijn de supercharged complexe getallen waar we het hierboven over hadden; we definiëren een nieuw “magisch getal ” �, gedefinieerd door een polynoom van de 12e graad zoals �12−18⋅�6+82=0)
• �� is het type object waar het resultaat van de elliptische curve in gaat. In de curven waar we naar kijken, is �� (��)12 (hetzelfde supercharged complexe getal als gebruikt in �2)

De belangrijkste eigenschap waaraan het moet voldoen is bilineariteit, wat in deze context betekent dat:

• �(�,�+�)=�(�,�)⋅�(�,�)
• �(�+�,�)=�(�,�)⋅�(�,�)

Er zijn nog twee andere belangrijke criteria:

• Efficiënte berekenbaarheid (We kunnen bijvoorbeeld een gemakkelijke koppeling maken door eenvoudigweg de discrete logaritmen van alle punten te nemen en ze met elkaar te vermenigvuldigen, maar dit is rekentechnisch net zo moeilijk als het doorbreken van elliptische curve-cryptografie, dus het telt niet)
• Niet-degeneratie (Natuurlijk, je zou gewoon �(�,�)=1 kunnen definiëren, maar dat is geen bijzonder nuttige combinatie)

Dus hoe doen we dit?

De wiskunde achter waarom koppelingsfuncties werken is behoorlijk lastig en vergt nogal wat geavanceerde algebra die zelfs verder gaat dan wat we tot nu toe hebben gezien, maar ik zal een schets geven. Allereerst moeten we het concept van a definiëren splitser, in feite een alternatieve manier om functies op elliptische curvepunten weer te geven. Een deler van een functie telt in principe de nullen en de oneindigheden van de functie. Laten we een paar voorbeelden bekijken om te zien wat dit betekent. Laten we een punt �=(��,��) vaststellen en de volgende functie bekijken:

�(�,�)=�−��

De deler is [�]+[−�]−2⋅[�] (de vierkante haakjes worden gebruikt om aan te geven dat we het hebben over de aanwezigheid van het punt � in de reeks nullen en oneindigheden van de functie, niet het punt P zelf; [�]+[�] is niet hetzelfde als [�+�]). De redenering is als volgt:

• De functie is gelijk aan nul bij �, aangezien � is ��, dus �−��=0
• De functie is gelijk aan nul bij −�, aangezien −� en � dezelfde �-coördinaat delen
• De functie gaat naar oneindig zoals � naar oneindig gaat, dus we zeggen dat de functie gelijk is aan oneindig bij �. Er is een technische reden waarom deze oneindigheid twee keer moet worden geteld, dus wordt � opgeteld met een “multipliciteit” van −2 (negatief omdat het een oneindigheid is en geen nul, twee vanwege deze dubbele telling).

De technische reden is grofweg deze: omdat de vergelijking van de curve �3=�2+� is, gaat deze “1.5 keer sneller” naar oneindig dan � zodat �2 gelijke tred houdt met �3; dus als een lineaire functie alleen � omvat, wordt deze weergegeven als een oneindigheid van veelheid 2, maar als deze � omvat, wordt deze weergegeven als een oneindigheid van veelheid 3.

Overweeg nu een "lijnfunctie":

��+��+�=0

Waarbij �, � en � zorgvuldig gekozen zijn, zodat de lijn door de punten � en � loopt. Vanwege de manier waarop elliptische curve-optelling werkt (zie het diagram bovenaan), betekent dit ook dat deze door −�−� gaat. En het gaat omhoog naar oneindig, afhankelijk van zowel � als �, dus de deler wordt [�]+[�]+[−�−�]−3⋅[�].

We weten dat elke “rationele functie” (dat wil zeggen een functie die alleen wordt gedefinieerd met behulp van een eindig aantal +,−,⋅ en / bewerkingen op de coördinaten van het punt) op unieke wijze overeenkomt met een deler, tot vermenigvuldiging met een constante (dwz. als twee functies � en � dezelfde deler hebben, dan is �=�⋅� voor een constante �).

Voor twee willekeurige functies � en � is de deler van �⋅� gelijk aan de deler van � plus de deler van � (in wiskundeboeken zie je (�⋅�)=(�)+(�)), dus bijvoorbeeld als �(�,�)=��−�, dan (�3)=3⋅[�]+3⋅[−�]−6⋅[�]; � en −� worden “drievoudig geteld” om rekening te houden met het feit dat �3 op die punten “drie keer zo snel” naar 0 nadert in een bepaalde wiskundige zin.

Merk op dat er een stelling bestaat die stelt dat als je “de vierkante haakjes verwijdert” van een deler van een functie, de punten opgeteld �([�]+[�]+[−�−�]−3⋅[ moeten zijn) �] past duidelijk, als �+�−�−�−3⋅�=�), en elke deler die deze eigenschap heeft, is de deler van een functie.

Nu zijn we klaar om naar Tate-koppelingen te kijken. Beschouw de volgende functies, gedefinieerd via hun delers:

• (��)=�⋅[�]−�⋅[�], waarbij � de orde van �1 is, dwz. �⋅�=� voor elke �
• (��)=�⋅[�]−�⋅[�]
• (�)=[�+�]−[�]−[�]+[�]

Laten we nu eens kijken naar het product ��⋅��⋅��. De deler is:

�⋅[�]−�⋅[�]+�⋅[�]−�⋅[�]+�⋅[�+�]−�⋅[�]−�⋅[�]+�⋅[�]

Wat netjes wordt vereenvoudigd tot:

�⋅[�+�]−�⋅[�]

Merk op dat deze deler precies hetzelfde formaat heeft als de deler voor �� en �� hierboven. Daarom ��⋅��⋅��=��+�.

Nu introduceren we een procedure die de stap “laatste machtsverheffing” wordt genoemd, waarbij we het resultaat van onze bovenstaande functies (��,��, enz.) nemen en dit verheffen tot de macht �=(�12−1)/�, waarbij �12−1 de volgorde is van de multiplicatieve groep in (��)12 (d.w.z. for elke �∈(��)12,�(�12−1)=1). Merk op dat als je deze machtsverheffing toepast op elk resultaat dat dat heeft al verheven tot de macht �, krijg je een machtsverheffing tot de macht �12−1, dus het resultaat wordt 1. Dus na de laatste machtsverheffing wordt �� opgeheven en krijgen we ���⋅���=( ��+�)�. Er is enige bilineariteit voor jou.

Als je nu een functie wilt maken die bilineair is in beide argumenten, moet je je verdiepen in griezeligere wiskunde, waarbij je in plaats van �� van een waarde rechtstreeks te nemen, �� van een waarde neemt splitser, en dat is waar de volledige “Tate-koppeling” vandaan komt. Om nog meer resultaten te bewijzen, moet je omgaan met begrippen als ‘lineaire gelijkwaardigheid’ en ‘Weil-wederkerigheid’, en vanaf daar gaat het konijnenhol verder. Over dit alles kunt u meer leesmateriaal vinden hier en hier.

Voor een implementatie van een aangepaste versie van de Tate-koppeling, de optimale Ate-koppeling genoemd, kijk hier. De code wordt geïmplementeerd Millers algoritme, wat nodig is om �� daadwerkelijk te berekenen.

Merk op dat het feit dat dit soort koppelingen mogelijk zijn enigszins een gemengde zegen is: aan de ene kant betekent het dat alle protocollen die we met koppelingen kunnen doen mogelijk worden, maar het betekent ook dat we voorzichtiger moeten zijn met welke elliptische curven we gebruiken.

Elke elliptische curve heeft een waarde die an wordt genoemd graad van inbedding; in wezen de kleinste � zodat ��−1 een veelvoud is van � (waarbij � het priemgetal is dat voor het veld wordt gebruikt en � de volgorde van de curve is). In de bovenstaande velden, �=12, en in de velden die worden gebruikt voor traditionele ECC (dat wil zeggen waar we ons niet druk maken over koppelingen), is de mate van inbedding vaak extreem groot, tot het punt dat koppelingen rekenkundig onhaalbaar zijn om te berekenen; Als we echter niet oppassen, kunnen we velden genereren waarbij �=4 of zelfs 1.

Als �=1, dan kan het “discrete logaritme”-probleem voor elliptische curven (in wezen het herstellen van � als je alleen het punt �=�⋅� kent, het probleem dat je moet oplossen om een ​​privésleutel van een elliptische curve te “kraken”) worden verminderd in een soortgelijk wiskundig probleem over ��, waar het probleem veel eenvoudiger wordt (dit wordt de MOV-aanval); het gebruik van curven met een inbeddingsgraad van 12 of hoger zorgt ervoor dat deze reductie ofwel niet beschikbaar is, ofwel dat het oplossen van het discrete logprobleem over koppelingsresultaten minstens net zo moeilijk is als het herstellen van een privésleutel uit een publieke sleutel “op de normale manier” (dat wil zeggen. rekenkundig onhaalbaar). Geen zorgen; alle standaardcurveparameters zijn grondig gecontroleerd op dit probleem.

Houd ons in de gaten voor een wiskundige uitleg over hoe zk-SNARK's werken, binnenkort beschikbaar.

Speciale dank aan Christian Reitwiessner, Ariel Gabizon (van Zcash) en Alfred Menezes voor het beoordelen en aanbrengen van correcties.

• Door SEO aangedreven content en PR-distributie. Word vandaag nog versterkt.
• PlatoData.Network Verticale generatieve AI. Versterk jezelf. Toegang hier.
• PlatoAiStream. Web3-intelligentie. Kennis versterkt. Toegang hier.
• PlatoESG. carbon, CleanTech, Energie, Milieu, Zonne, Afvalbeheer. Toegang hier.
• Plato Gezondheid. Intelligentie op het gebied van biotech en klinische proeven. Toegang hier.
• BlockOffsets. Eigendom voor milieucompensatie moderniseren. Toegang hier.
• Bron: Plato data-intelligentie.