Vitalik Buterin via Vitalik Buterins blogg

Detta är en spegel av inlägget kl https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627

Utlösande varning: matematik.

En av de viktigaste kryptografiska primitiven bakom olika konstruktioner, inklusive deterministiska tröskelsignaturer, zk-SNARKs och andra enklare former av noll-kunskapsbevis är den elliptiska kurvan. Elliptiska kurvpar (eller "bilinjära kartor") är ett nytt tillägg till en 30-årig historia av att använda elliptiska kurvor för kryptografiska applikationer inklusive kryptering och digitala signaturer; parningar introducerar en form av "krypterad multiplikation", vilket kraftigt utökar vad elliptiska kurvor-baserade protokoll kan göra. Syftet med den här artikeln kommer att vara att gå in på elliptiska kurvpar i detalj och förklara en allmän översikt över hur de fungerar.

Du förväntas inte förstå allt här första gången du läser det, eller ens tionde gången; det här är verkligen svårt. Men förhoppningsvis kommer denna artikel att ge dig åtminstone en liten uppfattning om vad som händer under huven.

Elliptiska kurvor i sig är mycket ett icke-trivialt ämne att förstå, och den här artikeln kommer i allmänhet att anta att du vet hur de fungerar; om du inte gör det rekommenderar jag den här artikeln här som en primer: https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/. Som en snabb sammanfattning, elliptisk kurvkryptografi involverar matematiska objekt som kallas "punkter" (dessa är bokstavliga tvådimensionella punkter med (�,�) koordinater), med speciella formler för att addera och subtrahera dem (dvs. för att beräkna koordinaterna för �= �+�), och du kan också multiplicera en punkt med ett heltal (dvs. �⋅�=�+�+…+�, även om det finns ett mycket snabbare sätt att beräkna det om � är stort).

Så här ser punkttillägg ut grafiskt.

Det finns en speciell punkt som kallas "punkten i oändligheten" (�), motsvarande noll i punktaritmetik; det är alltid så att �+�=�. Dessutom har en kurva en "beställa"; det finns ett tal � sådant att �⋅�=� för alla � (och naturligtvis �⋅(�+1)=�,�⋅(7⋅�+5)=�⋅5, och så vidare). Det finns också någon allmänt överenskommen "generatorpunkt" �, som förstås representera talet 1. Teoretiskt sett kan vilken punkt som helst på en kurva (förutom �) vara �; allt som spelar roll är att � är standardiserat.

Parningar går ett steg längre genom att de låter dig kontrollera vissa typer av mer komplicerade ekvationer på elliptiska kurvpunkter — till exempel om �=�⋅�,�=�⋅� och �=�⋅� kan du kontrollera om eller inte �⋅�=�, med bara �,� och � som indata. Det här kan tyckas som om de grundläggande säkerhetsgarantierna för elliptiska kurvor bryts, eftersom information om � läcker av att man bara känner till P, men det visar sig att läckaget är mycket begränsat - särskilt beslutande Diffie Hellman-problem är lätt, men det beräkningsmässiga Diffie Hellman-problemet (att känna till � och � i exemplet ovan, databehandling �=�⋅�⋅�) och diskret logaritmproblem (återhämta � från �) förblir beräkningsmässigt omöjliga (åtminstone om de var tidigare).

Ett tredje sätt att se på vad parningar gör, och ett som kanske är mest upplysande för de flesta användningsfall vi handlar om, är att om du ser elliptiska kurvpunkter som envägskrypterade tal (det vill säga ���� ���(�)=�⋅�=�), medan traditionell elliptisk kurva låter dig kontrollera linjär begränsningar för siffrorna (t.ex. om �=�⋅�,�=�⋅� och �=�⋅�, kontrollera 5⋅�+7⋅�=11⋅� är verkligen kontrollera att 5⋅�+7⋅�=11⋅�), kan parningar dig kontrollera kvadratisk begränsningar (t.ex. att kontrollera �(�,�)⋅�(�,�⋅5)=1 är verkligen kontrollerar att �⋅�+5=0). Och att gå upp till kvadratisk är tillräckligt för att låta oss arbeta med deterministiska tröskelsignaturer, kvadratiska aritmetiska program och allt annat bra.

Nu, vad är den här roliga �(�,�)-operatören som vi introducerade ovan? Det här är parningen. Matematiker kallar det också ibland för a bilinjär karta; ordet "bilinjär" betyder här i grunden att det uppfyller begränsningarna:

�(�,�+�)=�(�,�)⋅�(�,�)

�(�+�,�)=�(�,�)⋅�(�,�)

Observera att + och ⋅ kan vara godtyckliga operatorer; När du skapar tjusiga nya typer av matematiska objekt, bryr sig abstrakt algebra inte hur + och ⋅ är definierade, så länge de är konsekventa på vanliga sätt, t.ex. �+�=�+�,(�⋅�)⋅�=�⋅(�⋅�) och (�⋅�)+(�⋅�)=(�+�)⋅�.

Om �, �, � och � var enkla nummer, då är det lätt att göra en enkel parning: vi kan göra �(�,�)=2��. Då kan vi se:

�(3,4+5)=23⋅9=227

�(3,4)⋅�(3,5)=23⋅4⋅23⋅5=212⋅215=227

Det är bilinjärt!

Sådana enkla parningar är dock inte lämpliga för kryptografi eftersom objekten som de arbetar på är enkla heltal och är för lätta att analysera; heltal gör det enkelt att dividera, beräkna logaritmer och göra olika andra beräkningar; enkla heltal har inget begrepp om en "offentlig nyckel" eller en "envägsfunktion". Dessutom, med parningen som beskrivs ovan kan du gå bakåt – genom att veta � och veta �(�,�), kan du helt enkelt beräkna en division och en logaritm för att bestämma �. Vi vill ha matematiska objekt som är så nära "svarta lådor" som möjligt där du kan addera, subtrahera, multiplicera och dividera, men gör inget annat. Det är här elliptiska kurvor och elliptiska kurvpar kommer in.

Det visar sig att det är möjligt att göra en bilinjär karta över elliptiska kurvpunkter – det vill säga komma fram till en funktion �(�,�) där ingångarna � och � är elliptiska kurvpunkter, och där utdata är vad som kallas en (��)12 element (åtminstone i det specifika fallet vi kommer att täcka här; detaljerna skiljer sig beroende på detaljerna i kurvan, mer om detta senare), men matematiken bakom att göra det är ganska komplex.

Låt oss först täcka prime fields och extension fields. Den vackra elliptiska kurvan på bilden tidigare i det här inlägget ser bara ut så om du antar att kurvekvationen är definierad med hjälp av vanliga reella tal. Men om vi faktiskt använder vanliga reella tal i kryptografi, så kan du använda logaritmer för att "gå bakåt", och allt går sönder; Dessutom kan mängden utrymme som behövs för att faktiskt lagra och representera siffrorna växa godtyckligt. Därför använder vi istället siffror i a primärt fält.

Ett primtalsfält består av mängden siffror 0,1,2…�−1, där � är primtal, och de olika operationerna definieras enligt följande:

�+�:(�+�) % �

�⋅�:(�⋅�) % �

�−�:(�−�) % �

�/�:(�⋅��−2) % �

I princip görs all matematik modulo � (se här. för en introduktion till modulär matematik). Division är ett specialfall; normalt är 32 inte ett heltal, och här vill vi bara ta itu med heltal, så vi försöker istället hitta talet � så att �⋅2=3, där ⋅ givetvis syftar på modulär multiplikation enligt definitionen ovan. Tack vare Fermats lilla sats, exponentieringstricket som visas ovan gör jobbet, men det finns också ett snabbare sätt att göra det, med hjälp av Utökad euklidisk algoritm. Antag att �=7; här är några exempel:

2+3=5 % 7=5

4+6=10 % 7=3

2−5=−3 % 7=4

6⋅3=18 % 7=4

3/2=(3⋅25) % 7=5

5⋅2=10 % 7=3

Om du leker med den här typen av matematik kommer du att märka att den är helt konsekvent och uppfyller alla vanliga regler. De två sista exemplen ovan visar hur (�/�)⋅�=�; du kan också se att (�+�)+�=�+(�+�),(�+�)⋅�=�⋅�+�⋅� och alla andra algebraiska gymnasieidentiteter du känner och älskar fortsätter att hålla sant också. I elliptiska kurvor i verkligheten beräknas punkterna och ekvationerna vanligtvis i primtalsfält.

Låt oss prata om det förlängningsfält. Du har förmodligen redan sett ett tilläggsfält tidigare; det vanligaste exemplet som du stöter på i matteläroböcker är fältet för komplexa tal, där fältet för reella tal är "utvidgat" med tilläggselementet −1=�. I grund och botten fungerar tilläggsfält genom att ta ett befintligt fält, sedan "uppfinna" ett nytt element och definiera förhållandet mellan det elementet och befintliga element (i det här fallet �2+1=0), och se till att denna ekvation inte stämmer. för alla tal som finns i det ursprungliga fältet, och titta på mängden av alla linjära kombinationer av element i det ursprungliga fältet och det nya elementet som du just har skapat.

Vi kan också göra förlängningar av prime fields; till exempel kan vi utöka primfältet mod7 som vi beskrev ovan med �, och sedan kan vi göra:

(2+3�)+(4+2�)=6+5�

(5+2�)+3=1+2�

(6+2�)⋅2=5+4�

4�⋅(2+�)=3+�

Det sista resultatet kan vara lite svårt att räkna ut; det som hände där var att vi först bryter ner produkten till 4�⋅2+4�⋅�, vilket ger 8�−4, och sedan för att vi arbetar i mod7 matte blir det �+3. För att dela upp gör vi:

�/�:(�⋅�(�2−2)) % �

Observera att exponenten för Fermats lilla teorem nu är �2 istället för �, men om vi vill bli mer effektiva kan vi också istället utöka den utökade euklidiska algoritmen för att göra jobbet. Observera att ��2−1=1 för alla � i detta fält, så vi kallar �2−1 för "ordningen för den multiplikativa gruppen i fältet".

Med reella tal, den Algebras grundläggande sats säkerställer att den kvadratiska förlängningen som vi kallar de komplexa talen är "fullständig" - du kan inte utöka den ytterligare, eftersom för vilket matematiskt samband (åtminstone, vilket matematiskt samband som helst definierat av en algebraisk formel) som du kan komma på mellan något nytt element � och de befintliga komplexa talen, är det möjligt att komma på minst ett komplext tal som redan uppfyller det förhållandet. Men med primfält har vi inte det här problemet, så vi kan gå längre och göra kubiska förlängningar (där det matematiska förhållandet mellan något nytt element � och befintliga fältelement är en kubikekvation, så 1,� och �2 är alla linjärt oberoende av varandra), förlängningar av högre ordning, förlängningar av förlängningar, etc. Och det är dessa typer av överladdade modulära komplexa tal som elliptiska kurvpar bygger på.

För dem som är intresserade av att se den exakta matematiken som är involverad i att göra alla dessa operationer skrivna i kod, implementeras primfält och fälttillägg här: https://github.com/ethereum/py_pairing/blob/master/py_ecc/bn128/bn128_field_elements.py

Nu till elliptiska kurvpar. En elliptisk kurvparning (eller snarare, den specifika formen av parning vi ska utforska här; det finns också andra typer av parningar, även om deras logik är ganska lik) är en karta �2×�1→��, där:

• �1 är en elliptisk kurva, där punkter uppfyller en ekvation av formen �2=�3+�, och där båda koordinaterna är element i �� (dvs. de är enkla tal, förutom aritmetiken görs modulo något primtal)
• �2 är en elliptisk kurva, där punkter uppfyller samma ekvation som �1, förutom där koordinaterna är element av (��)12 (dvs. de är de överladdade komplexa talen vi pratade om ovan; vi definierar ett nytt "magiskt tal" ” �, som definieras av ett 12:e gradens polynom som �12−18⋅�6+82=0)
• �� är den typ av objekt som resultatet av den elliptiska kurvan går in i. I kurvorna som vi tittar på är �� (��)12 (samma överladdade komplexa tal som används i �2)

Den huvudsakliga egenskapen som den måste uppfylla är bilinearitet, vilket i detta sammanhang innebär att:

• �(�,�+�)=�(�,�)⋅�(�,�)
• �(�+�,�)=�(�,�)⋅�(�,�)

Det finns två andra viktiga kriterier:

• Effektiv beräkningsbarhet (t.ex. vi kan göra en enkel parning genom att helt enkelt ta de diskreta logaritmerna för alla punkter och multiplicera dem tillsammans, men detta är lika svårt beräkningsmässigt som att bryta elliptisk kurvkryptografi i första hand, så det räknas inte)
• Icke-degeneration (visst, du kan bara definiera �(�,�)=1, men det är inte en särskilt användbar koppling)

Så hur gör vi det här?

Matematiken bakom varför parningsfunktioner fungerar är ganska knepig och involverar en hel del avancerad algebra som går utöver vad vi har sett hittills, men jag ska ge en översikt. Först och främst måste vi definiera begreppet a delare, i grunden ett alternativt sätt att representera funktioner på elliptiska kurvpunkter. En divisor för en funktion räknar i princip funktionens nollor och oändligheter. För att se vad detta betyder, låt oss gå igenom några exempel. Låt oss fixa en punkt �=(��,��) och överväga följande funktion:

�(�,�)=�−��

Divisorn är [�]+[−�]−2⋅[�] (hakparenteserna används för att representera det faktum att vi syftar på närvaron av punkten � i uppsättningen av nollor och oändligheter av funktionen, inte själva punkten P; [�]+[�] är inte samma sak som [�+�]). Resonemanget är som följer:

• Funktionen är lika med noll vid �, eftersom � is ��, alltså �−��=0
• Funktionen är lika med noll vid −�, eftersom −� och � delar samma � koordinat
• Funktionen går till oändlighet som � går till oändlighet, så vi säger att funktionen är lika med oändlighet vid �. Det finns en teknisk anledning till att denna oändlighet måste räknas två gånger, så � läggs till med en "multiplikhet" på −2 (negativ eftersom det är en oändlighet och inte en nolla, två på grund av denna dubbelräkning).

Det tekniska skälet är ungefär detta: eftersom ekvationen för kurvan är �3=�2+�, går det till oändligheten "1.5 gånger snabbare" än � gör för att �2 ska hänga med �3; därför, om en linjär funktion bara inkluderar � så representeras den som en oändlighet av multiplicitet 2, men om den inkluderar � så representeras den som en oändlighet av multiplicitet 3.

Tänk nu på en "linjefunktion":

��+��+�=0

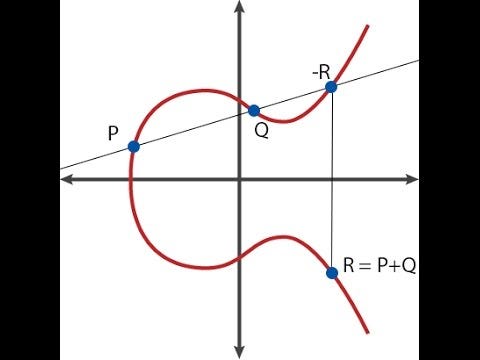
Där �, � och � är noggrant valda så att linjen går genom punkterna � och �. På grund av hur elliptisk kurvaddition fungerar (se diagrammet längst upp) betyder det också att den går genom −�−�. Och det går upp till oändligheten beroende på både � och �, så divisorn blir [�]+[�]+[−�−�]−3⋅[�].

Vi vet att varje "rationell funktion" (dvs. en funktion definierad endast med ett ändligt antal +,−,⋅ och / operationer på punktens koordinater) unikt motsvarar någon divisor, upp till multiplikation med en konstant (dvs. om två funktioner � och � har samma divisor, då �=�⋅� för någon konstant �).

För två valfria funktioner � och � är divisorn för �⋅� lika med divisorn för � plus divisorn för � (i matteläroböcker ser du (�⋅�)=(�)+(�)), så till exempel om �(�,�)=��−�, då (�3)=3⋅[�]+3⋅[−�]−6⋅[�]; � och −� är "trippelräknade" för att förklara det faktum att �3 närmar sig 0 vid dessa punkter "tre gånger så snabbt" i en viss matematisk mening.

Observera att det finns ett teorem som säger att om du "tar bort hakparenteserna" från en divisor för en funktion, måste punkterna summeras till �([�]+[�]+[−�−�]−3⋅[ �] passar tydligt, som �+�−�−�−3⋅�=�), och varje divisor som har denna egenskap är divisor för en funktion.

Nu är vi redo att titta på Tate-parningar. Tänk på följande funktioner, definierade via deras divisorer:

• (��)=�⋅[�]−�⋅[�], där � är ordningen på �1, dvs. �⋅�=� för alla �
• (��)=�⋅[�]−�⋅[�]
• (�)=[�+�]−[�]−[�]+[�]

Nu ska vi titta på produkten ��⋅��⋅��. Divisorn är:

�⋅[�]−�⋅[�]+�⋅[�]−�⋅[�]+�⋅[�+�]−�⋅[�]−�⋅[�]+�]⋅[

Vilket förenklar snyggt till:

�⋅[�+�]−�⋅[�]

Observera att denna divisor har exakt samma format som divisorn för �� och �� ovan. Därför ��⋅��⋅��=��+�.

Nu introducerar vi en procedur som kallas "slutlig exponentieringssteget", där vi tar resultatet av våra funktioner ovan (��,��, etc.) och höjer det till potensen �=(�12−1)/�, där �12−1 är ordningen för den multiplikativa gruppen i (��)12 (dvs. för vilken som helst �∈(��)12,�(�12−1)=1). Observera att om du tillämpar denna exponentiering på något resultat som har redan har höjts till �, får du en exponentiering till �12−1, så resultatet blir 1. Följaktligen, efter slutlig exponentiering, avbryts �� och vi får ���⋅���=( ��+�)�. Det finns lite bilinearitet för dig.

Om du nu vill göra en funktion som är bilinjär i båda argumenten måste du gå in på spöklikare matematik, där du istället för att ta �� av ett värde direkt, tar �� av en delare, och det är därifrån hela "Tate-parningen" kommer. För att bevisa några fler resultat måste du hantera begrepp som "linjär ekvivalens" och "Weil reciprocity", och kaninhålet fortsätter därifrån. Du kan hitta mer läsmaterial om allt detta här. och här..

För en implementering av en modifierad version av Tate-parningen, kallad optimal Ate-paring, kolla här. Koden implementerar Millers algoritm, som behövs för att faktiskt beräkna ��.

Observera att det faktum att parningar som denna är möjliga är lite av en blandad välsignelse: å ena sidan betyder det att alla protokoll vi kan göra med parningar blir möjliga, men det betyder också att vi måste vara mer försiktiga med vilka elliptiska kurvor vi använder.

Varje elliptisk kurva har ett värde som kallas an inbäddningsgrad; i huvudsak den minsta � så att ��−1 är en multipel av � (där � är primtal som används för fältet och � är kurvordningen). I fälten ovan, �=12, och i fälten som används för traditionell ECC (dvs. där vi inte bryr oss om parningar), är inbäddningsgraden ofta extremt stor, till den grad att parningar är beräkningsmässigt omöjliga att beräkna; Men om vi inte är försiktiga kan vi generera fält där �=4 eller till och med 1.

Om �=1, så kan problemet med "diskret logaritm" för elliptiska kurvor (i huvudsak återhämta sig � att bara känna till punkten �=�⋅�, problemet som du måste lösa för att "spricka" en elliptisk kurva privat nyckel) reduceras till ett liknande matematiskt problem över ��, där problemet blir mycket lättare (detta kallas MOV attack); att använda kurvor med en inbäddningsgrad på 12 eller högre säkerställer att denna minskning antingen är otillgänglig eller att det är minst lika svårt att lösa det diskreta loggproblemet över parningsresultat som att återställa en privat nyckel från en offentlig nyckel "på normalt sätt" (dvs. beräkningsmässigt omöjligt). Oroa dig inte; alla standardkurvparametrar har kontrollerats noggrant för detta problem.

Håll ögonen öppna för en matematisk förklaring av hur zk-SNARKs fungerar, kommer snart.

Speciellt tack till Christian Reitwiessner, Ariel Gabizon (från Zcash) och Alfred Menezes för att ha granskat och gjort korrigeringar.

• SEO-drivet innehåll och PR-distribution. Bli förstärkt idag.
• PlatoData.Network Vertical Generative Ai. Styrka dig själv. Tillgång här.
• PlatoAiStream. Web3 Intelligence. Kunskap förstärkt. Tillgång här.
• Platoesg. Kol, CleanTech, Energi, Miljö, Sol, Avfallshantering. Tillgång här.
• PlatoHealth. Biotech och kliniska prövningar Intelligence. Tillgång här.
• BlockOffsets. Modernisera miljökompensation ägande. Tillgång här.
• Källa: Platon Data Intelligence.