Beskrivning
I den här artikeln kommer vi att utforska vad som är hypotesprövning, med fokus på formuleringen av noll- och alternativhypoteser, sätta upp hypotestest och vi kommer att djupdyka i parametriska och icke-parametriska tester, diskutera deras respektive antaganden och implementering i python. Men vårt huvudfokus kommer att ligga på icke-parametriska tester som Mann-Whitney U-testet och Kruskal-Wallis-testet. I slutet kommer du att ha en omfattande förståelse för hypotestestning och de praktiska verktygen för att tillämpa dessa begrepp i dina egna statistiska analyser.
Inlärningsmål
- Förstå principerna för hypotesprövning, inklusive formulering av noll- och alternativhypoteser.
- Uppsättning av hypotestest.
- Förståelse om parametriskt test och dess typer.
- Förståelse om icke-parametriska test och dess typer tillsammans med dess implementeringar.
- Skillnaden mellan parametrisk och icke-parametrisk.
Innehållsförteckning
Vad är hypotestestning?
Hypotes är ett påstående från en person/organisation. Påståendet handlar vanligtvis om populationsparametrar som medelvärde eller proportion och vi söker bevis från ett urval för att stödja påståendet.
Hypotestestning, ibland kallad signifikanstestning, är en metod för att bekräfta ett påstående eller hypotes om en parameter i en population med hjälp av data som mäts i ett urval. Med den här metoden utforskar vi flera teorier genom att bestämma potentialen att om populationsparameterhypotesen hade varit sann, skulle en provstatistik kunna ha valts ut.
Hypotestestning innebär formulering av två hypoteser:
- Nollhypotes (H0)
- Alternativ hypotes (H1)
Nollhypotesen : Det är vanligtvis en hypotes om ingen skillnad och brukar betecknas med H0. Enligt RA Fisher är nollhypotes den hypotes som testas för eventuellt förkastande under antagandet att den är sann (Ref Fundamentals of Mathematical Statistics).
Alternativ hypotes: Varje hypotes som är komplementär till nollhypotesen kallas en alternativ hypotes, vanligtvis betecknad med H1.
Syftet med hypotestestning är att antingen förkasta eller behålla en nollhypotes för att fastställa ett statistiskt signifikant samband mellan två variabler (vanligtvis en oberoende och en beroende variabel, dvs vanligtvis en är orsaken och en är effekten).
Uppsättning av hypotestest
- Beskriv hypotesen i ord eller gör ett påstående.
- Baserat på krav definiera noll- och alternativa hypoteser.
- Identifiera vilken typ av hypotestest som är lämplig för påståendet ovan.
- Identifiera teststatistiken som ska användas för att testa nollhypotesens giltighet.
- Bestäm kriterierna för förkastande och bibehållande av nollhypotes. Detta kallas signifikansvärde som traditionellt betecknas med symbolen α (alfa).
- Beräkna p-värdet som är den villkorade sannolikheten för att observera teststatistikvärdet när nollhypotesen är sann. Enkelt uttryckt är p-värde beviset till stöd för nollhypotesen.
Parametriskt och icke-parametriskt test
Icke-parametriska statistiska tester förlitar sig inte på antaganden om parametrarna för populationsfördelningarna från vilka data samplas, medan parametriska statistiska test gör det.
Parametriska tester
De flesta statistiska tester utförs med en uppsättning antaganden som grund. Analysen kan ge missvisande eller helt falska slutsatser när vissa antaganden bryts.
Vanligtvis är antagandena:
- Normalitet: Samplingsfördelningen av parametrar som ska testas följer en normal (eller åtminstone symmetrisk) fördelning.
- Variansernas homogenitet: Variansen i data är densamma mellan olika grupper om vi inte testar för populationsmedel som kommer från två olika populationer.
Några av de parametriska testerna är:
- Z-test: Testa för populationsmedelvärde eller varians eller proportion när populationens standardavvikelse är känd.
- Elevens t-test: Testa för populationsmedelvärde eller varians eller proportion när populationens standardavvikelse inte är känd.
- Parat t-test: Används för att jämföra medelvärdena för två relaterade grupper eller tillstånd.
- Variansanalys (ANOVA): Används för att jämföra medel mellan tre eller flera oberoende grupper.
- Regressionsanalys: Används för att bedöma sambandet mellan en eller flera oberoende variabler och en beroende variabel.
- Analys av kovarians (ANCOVA): Utökar ANOVA genom att införliva ytterligare kovariater i analysen.
- Multivariat variansanalys (MANOVA): Utökar ANOVA för att bedöma skillnader i flera beroende variabler över grupper.
Låt oss nu djupdyka in i icke-parametriskt test.
Icke parametriskt test
För första gången använde Wolfowitz termen "icke-parametrisk" 1942. För att förstå idén om icke-parametrisk statistik måste man först ha en grundläggande förståelse för parametrisk statistik, som vi just har diskuterat. A parametriskt test kräver ett urval som följer en specifik fördelning (vanligtvis normal). Dessutom är icke-parametriska tester oberoende av parametriska antaganden som normalitet.
Icke-parametriska test (även känd som distributionsfria test eftersom de inte har antaganden om populationens fördelning). Icke-parametriska tester innebär att testerna inte är baserade på antagandena att data hämtas från en sannolikhetsfördelning definieras genom parametrar som medelvärde, proportion och standardavvikelse.
Icke-parametriska tester används när antingen:
- Testet handlar inte om populationsparametern som medelvärde eller proportion.
- Metoden kräver inga antaganden om befolkningsfördelning (som att befolkningen följer en normalfördelning).
Typer av icke-parametriska tester
Låt oss nu diskutera konceptet och proceduren för att göra Chi-Square-test, Mann-Whitney-test, Wilcoxon Signed Rank-test och Kruskal-Wallis-test:
Chi-Square-test
För att avgöra om sambandet mellan två kvalitativa variabler är statistiskt signifikant måste man genomföra ett signifikanstest som kallas Chi-Square Test.
Det finns två huvudtyper av Chi-Square-tester:
Chi-Square Goodness-of-Fit
Använd goodness-of-fit-testet för att avgöra om en population med en okänd fördelning "passar" med en känd fördelning. I detta fall kommer det att finnas en enda kvalitativ undersökningsfråga eller ett enda resultat av ett experiment från en enda population. Goodness-of-Fit används vanligtvis för att se om populationen är enhetlig (alla utfall inträffar med samma frekvens), populationen är normal eller populationen är densamma som en annan population med en känd fördelning. Noll- och alternativhypoteserna är:
- H0: Populationen passar den givna fördelningen.
- Ha: Populationen passar inte den givna fördelningen.
Låt oss förstå detta med ett exempel
| Dag | Måndag | Tisdag | Onsdag | Torsdag | Fredag | lördag | Söndag |
| Antal haverier | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
Tabellen visar antalet uppdelningar i en faktor. I det här exemplet finns bara en enskild variabel och vi måste avgöra om den observerade fördelningen (given i tabellen) passar den förväntade fördelningen eller inte.
För detta kommer nollhypotesen och alternativhypotesen att formuleras som:
- H0:Fördelningar är jämnt fördelade.
- Ha: Uppdelningar är inte jämnt fördelade.
Och frihetsgraden kommer att vara n-1 (i detta fall n=7, så df = 7-1=6)
Expected value will be= (14+22+16+18+12+19+11)/7=16
| Dag | Måndag | Tisdag | Onsdag | Torsdag | Fredag | lördag | Söndag |
| Antal uppdelningar (observerade) | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
| förväntat | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| (observerat-förväntat) | -2 | 6 | 0 | 2 | -4 | 3 | -5 |
| (observerat-förväntat)^2 | 4 | 36 | 0 | 4 | 16 | 9 | 25 |
Använd denna formel Beräkna chi-kvadrat
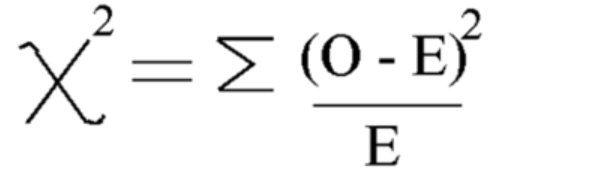
Chi-kvadrat = 5.875
Och frihetsgraden är = n-1=7-1=6
Låt oss nu se det kritiska värdet från chi square distributionstabell vid 5 % signifikansnivå
Så det kritiska värdet är 12.592
Eftersom det beräknade chi-kvadratvärdet är mindre än det kritiska värdet accepterar vi nollhypotesen och kan dra slutsatsen att uppdelningarna är likformigt fördelade.
Chi-Square Independence of Test
Använd testet för oberoende för att avgöra om två variabler (faktorer) är oberoende eller beroende, dvs om dessa två variabler har ett signifikant samband mellan dem eller inte. I detta fall kommer det att finnas två kvalitativa enkätfrågor eller experiment och en beredskapstabell kommer att konstrueras. Målet är att se om de två variablerna är orelaterade (oberoende) eller relaterade (beroende). Noll- och alternativhypoteserna är:
- H0: De två variablerna (faktorerna) är oberoende.
- Ha: De två variablerna (faktorerna) är beroende.
Låt oss ta ett exempel
Exempel där vi vill undersöka om kön och föredragen färg på skjortan var oberoende. Det betyder att vi vill ta reda på om en persons kön påverkar deras färgval. Vi gjorde en undersökning och organiserade uppgifterna i tabellen.
Denna tabell är observerade värden:
| Svart | White | Red | Blå | |
| man | 48 | 12 | 33 | 57 |
| Kvinna | 34 | 46 | 42 | 26 |
Formulera nu först noll- och alternativhypoteser
- H0: Kön och önskad skjortfärg är oberoende
- Ha: Kön och önskad skjortfärg är inte oberoende
För att beräkna Chi-kvadratteststatistik måste vi beräkna det förväntade värdet. Så lägg till alla rader och kolumner och totalsummor:
| Svart | White | Red | Blå | Totalt | |
| man | 48 | 12 | 33 | 57 | 150 |
| Kvinna | 34 | 46 | 42 | 26 | 148 |
| Totalt | 82 | 58 | 75 | 83 | 298 |
Efter detta kan vi beräkna förväntad värdetabell från tabellen ovan för varje post med denna formel = (rad total * kolumn total)/total total
Tabell för förväntat värde:
| Svart | White | Red | Blå | |
| man | 41.3 | 29.2 | 37.8 | 41.8 |
| Kvinna | 40.7 | 28.8 | 37.2 | 41.2 |
Beräkna nu Chi-kvadratvärde med formeln för chi-kvadrattest:
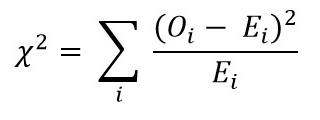
- Oi = observerat värde
- Ei = Förväntat värde
Värdet som vi får är: Χ2 = 34.9572
Beräkna frihetsgrad
DF=(nummer på rad-1)*(nummer på kolumn-1)
Hitta och jämför nu det kritiska värdet med chi-kvadrattestet statistiskt värde:
För att göra detta kan du slå upp frihetsgraden och signifikansnivån (alfa) från chi-kvadratfördelningstabell
Vid alfa =0.050 får vi kritiskt värde = 7.815
Eftersom chi-kvadrat> kritiskt värde
Därför förkastar vi nollhypotesen och vi kan dra slutsatsen att kön och föredragen skjortfärg inte är oberoende.
Implementering av Chi- Square
Låt oss nu se implementeringen av Chi-Square med hjälp av några verkliga exempel i python:
- H0: Kön och önskad skjortfärg är oberoende
- Ha: Kön och önskad skjortfärg är inte oberoende
Skapa datauppsättning:
import pandas as pd
from scipy.stats import chi2_contingency
from scipy.stats import chi2
# Given dataset
df_dict = {
'Black': [48, 34],
'White': [12, 46],
'Red': [33, 42],
'Blue': [57, 26]
}
dataset_table = pd.DataFrame(df_dict, index=['Male', 'Female'])
print("Dataset Table:")
print(dataset_table)
print()
# Observed Values
Observed_Values = dataset_table.values
print("Observed Values:")
print(Observed_Values)
print()
# Perform chi-square test
val = chi2_contingency(dataset_table)
Expected_Values = val[3]
print("Expected Values:")
print(Expected_Values)
print()
# Degree of Freedom
no_of_rows = len(dataset_table.iloc[0:2, 0])
no_of_columns = 4
ddof = (no_of_rows - 1) * (no_of_columns - 1)
print("Degree of Freedom:", ddof)
print()
# Chi-square statistic
chi_square = sum([(o - e) ** 2. / e for o, e in zip(Observed_Values, Expected_Values)])
chi_square_statistic = chi_square[0] + chi_square[1]
print("Chi-square statistic:", chi_square_statistic)
print()
# Critical value
alpha = 0.05
critical_value = chi2.ppf(q=1-alpha, df=ddof)
print('Critical value:', critical_value)
print()
# p-value
p_value = 1 - chi2.cdf(x=chi_square_statistic, df=ddof)
print('p-value:', p_value)
print()
# Significance level
print('Significance level:', alpha)
print('p-value:', p_value)
print('Degree of Freedom:', ddof)
print()
# Hypothesis testing
if chi_square_statistic >= critical_value:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
print()
if p_value <= alpha:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
Produktion:
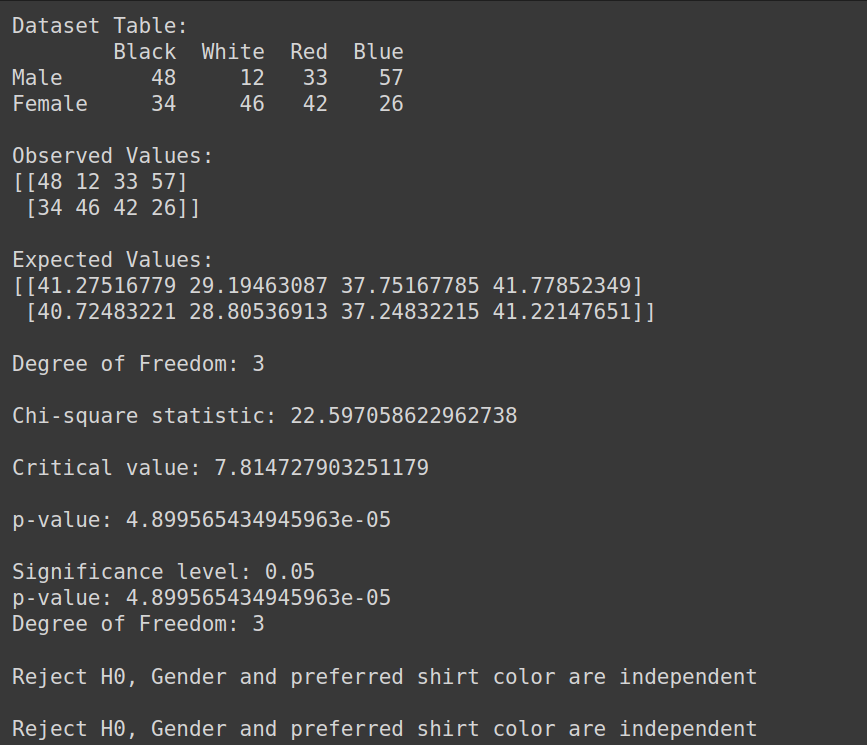
Mann- Whitney U Test
Mann-Whitney U-testet fungerar som det icke-parametriska alternativet till det oberoende provet t-testet. Den jämför två urvalsmedelvärden från samma population och avgör om de är lika. Detta test används vanligtvis för ordinaldata eller när antaganden för t-testet inte uppfylls.
Mann-Whitney U-testet rangordnar alla värden från båda grupperna tillsammans och summerar sedan rangorden för varje grupp. Den beräknar teststatistiken, U, baserat på dessa rangordningar. U-statistiken jämförs med ett kritiskt värde från en tabell eller beräknas med hjälp av en approximation. Om U-statistiken är mindre än det kritiska värdet förkastas nollhypotesen.
Detta skiljer sig från parametriska tester som t-testet, som jämför medelvärden och antar en normalfördelning. Mann-Whitney U-testet jämför istället rangordningar och kräver inte antagandet om en normalfördelning.
Att förstå Mann-Whitney U-testet kan vara svårt eftersom resultaten presenteras i grupprankningsskillnader snarare än gruppmedelskillnader.
Formel för Mann-Whitney Test:
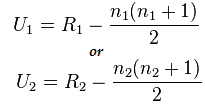
U= min(U1,U2)
Här,
- U= Mann-Whitney U Test
- n1= provstorlek ett
- n2= provstorlek två
- R1= Rang för provstorlek ett
- R2= Rang av provstorlek 2
Så låt oss förstå detta med ett kort exempel:
Anta att vi vill jämföra effektiviteten hos två olika behandlingsmetoder (metod A och metod B) för att förbättra patienternas hälsa. Vi har följande data:
- Metod A: 3,4,2,6,2,5
- Metod B: 9,7,5,10,6,8
Här kan vi se att data inte är normalfördelade, och urvalsstorlekarna är små.
Implementering av Mann-Whitney U-test
Låt oss nu utföra Mann-Whitney U-testet:
Men låt oss först formulera noll- och alternativhypotesen
- H0: Det finns ingen skillnad mellan rangen för varje behandling
- Ha: Det finns en skillnad mellan rangen för varje behandling
Kombinera alla behandlingar: 3,4,2,6,2,5,9,7,5,10,6,8
Sorterade data: 2,2,3,4,5,5,6,6,7,8,9,10
Rang av sorterade data: 1,2,3,4,5,6,7,8,9,10,11,12
- Rangordna data separat:
- Method A: 3(3),4(4),2(1.5),6(7.5),2(1.5),5(5.5)
- Method B: 9(11),7(9),5(5.5),10(12),6(1.5),8(10)
- Beräknar summan av rang):
- R1: 3+4+1.5+7.5+1.5+5.5=23
- R2: 11+9+5.5+12+1.5+10=55
Beräkna nu det statistiska värdet med denna formel:
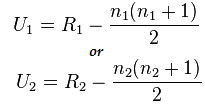
Här är n1=6 och n2=6
Och värdet efter beräkning för U1=2 och för U2= 34
Beräknar U-statistik:
Us= min(U1,U2)= min(2,34)= 2
Från Mann-Whitney bord vi kan hitta det kritiska värdet
I det här fallet blir det kritiska värdet 5
Eftersom Uc= 5 vilket är större än Oss vid 5 % signifikansnivå. Så vi avvisar H0
Därför kan vi dra slutsatsen att det finns en skillnad mellan rangen för varje behandling.
Implementering med python
from scipy.stats import mannwhitneyu, norm
import numpy as np
TreatmentA = np.array([3,4,2,6,2,5])
TreatmentB = np.array([9,7,5,10,6,8])
# Perform Mann-Whitney U test
U_statistic, p_value = mannwhitneyu(TreatmentA, TreatmentB)
# Print the result
print(f'The U-statistic is {U_statistic:.2f} and the p-value is {p_value:.4f}')
if p_value < 0.05:
print("Reject Null Hypothesis: There is a significant difference between the Rank of each treatment.")
else:
print("Fail to Reject Null Hypothesis: Fail to Reject Null Hypothesis: There is no enough evidence to conclude that there is difference between the Rank of each treatment")Produktion:

Kruskal –Wallis test
Kruskal –Wallis Test används med flera grupper. Det är det icke-parametriska och ett värdefullt alternativ till ett envägs ANOVA-test när antagandena om normalitet och varianslikhet bryts. Kruskal –Wallis Test jämför medianvärden för mer än två oberoende grupper.
Den testar nollhypotesen när k oberoende urval (k>=3) dras från en population med identiska fördelningar, utan att kräva normalitetsvillkoret för populationerna.
Antaganden:
Se till att det finns minst tre oberoende dragna stickprov. Varje prov har minst 5 observationer, n>=5
Betrakta ett exempel där vi vill avgöra om studietekniken som används av tre grupper av studenter påverkar deras provresultat. Vi kan använda Kruskal-Wallis-testet för att analysera data och bedöma om det finns statistiskt signifikanta skillnader i provresultat mellan grupperna.
Formulera nollhypotesen för detta som:
- H0: Det finns ingen skillnad i provresultat mellan de tre grupperna av elever.
- Ha: Det finns en skillnad i provresultat mellan de tre grupperna av elever.
Wilcoxon signerade rangtest
Wilcoxon Signed Rank Test (även känt som Wilcoxon Matched Pair Test) är den icke-parametriska versionen av beroende prov t-test eller parat prov t-test. Teckentest är det andra icke-parametriska alternativet till det parade provets t-test. Det används när variablerna av intresse är dikotoma till sin natur (som man och kvinna, ja och nej). Wilcoxon Signed Rank Test är också en icke-parametrisk version för ett prov t-test. Wilcoxon Signed Rank Test jämför medianerna för grupperna under två situationer (parade prover) eller så jämför det gruppens median med den hypoteserade medianen (ett prov).
Låt oss förstå detta med ett exempel, anta att vi har data om rökares dagliga cigarettkonsumtion före och efter deltagande i ett 8-veckors program och vi vill avgöra om det finns en signifikant skillnad i den dagliga cigarettkonsumtionen före och efter programmet. använd detta test
Hypotesformuleringen för detta blir
- H0: Det är ingen skillnad i daglig cigarettkonsumtion före och efter programmet.
- Ha: Det är skillnad i daglig cigarettkonsumtion före och efter programmet
Testa för normalitet
Låt oss nu diskutera normalitetstester:
Shapiro Wilk test
Shapiro-Wilk-testet bedömer om ett givet urval av data kommer från en normalfördelad population. Det är ett av de vanligaste testerna för att kontrollera normalitet. Testet är särskilt användbart när det handlar om relativt små urvalsstorlekar.
I Shapiro-Wilk-testet:
- Nollhypotesen : Urvalsdata kommer från en population som följer en normalfördelning.
- Alternativ hypotes : Urvalsdata kommer inte från en population som följer en normalfördelning.
Teststatistiken som genereras av Shapiro-Wilk-testet mäter diskrepansen mellan observerade data och förväntade data under antagande om normalitet. Om p-värdet associerat med teststatistiken är mindre än en vald signifikansnivå (t.ex. 0.05), förkastar vi nollhypotesen, vilket indikerar att data inte är normalfördelade. Om p-värdet är större än signifikansnivån misslyckas vi med att förkasta nollhypotesen, vilket tyder på att data kan följa en normalfördelning.
Låt oss först skapa en datauppsättning för dessa test du kan använda vilken datauppsättning du vill:
import pandas as pd
# Create the dictionary with the provided data
data = {
'population': [6.1101, 5.5277, 8.5186, 7.0032, 5.8598],
'profit': [17.5920, 9.1302, 13.6620, 11.8540, 6.8233]
}
# Create the DataFrame
df = pd.DataFrame(data)
response_var=df['profit']
Here, a sample for running Shapiro -Wilk test on python:
from scipy.stats import shapiro
stat, p_val = shapiro(response_var)
print(f'Shapiro-Wilk Test: Statistic={stat} p-value={p_val}')
if p_val > alpha:
print('Data looks normal (fail to reject H0)')
else:
print('Data looks normal (fail to reject H0)')Produktion:

Detta test är mest lämpligt för relativt små urvalsstorlekar (n=< 50-2000) eftersom det blir mindre tillförlitligt med större urvalsstorlekar.
Andersson-Darling
Den bedömer om ett givet urval av data kommer från en specificerad fördelning, till exempel normalfördelningen. Det liknar Shapiro-Wilk-testet men är känsligare speciellt för mindre provstorlekar.
Den passar flera fördelningar, inklusive normalfördelningen, för fall där fördelningens parametrar är okända.
Här, Python-kod för att implementera det:
from scipy.stats import anderson
response_var = data['profit']
alpha = 0.05
# Anderson-Darling Test
result = anderson(response_var)
print(f'Anderson statistics: {result.statistic:.3f}')
if result.statistic > result.critical_values[-1]:
p_value = 0.0 # The p-value is essentially 0 if the statistic exceeds the largest critical value
else:
p_value = result.significance_level[result.statistic < result.critical_values][-1]
print("P-value:", p_value)
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")Produktion:

Jarque-Bera test
Jarque-Bera-testet bedömer om ett givet urval av data kommer från en normalfördelad population. Det är baserat på datas skevhet och kurtos.
Här är implementeringen av Jarque-Bera Test i Python med exempeldata:
from scipy.stats import jarque_bera
# Performing Jarque-Bera test
test_statistic, p_value = jarque_bera(response_var)
print("Jarque-Bera Test Statistic:", test_statistic)
print("P-value:", p_value)
# Interpreting results
alpha = 0.05
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")Produktion:

| Kategori | Parametriska statistiska tekniker | Icke-parametrisk statistiktekniker |
| korrelation | Pearson Product Moment Korrelationskoefficient (r) | Spearman Rank Coefficient Correlation (Rho), Kendall's Tau |
| Två grupper, oberoende åtgärder | Oberoende t-test | Mann-Whitney U-test |
| Mer än två grupper, oberoende åtgärder | Envägs ANOVA | Kruskal-Wallis enkelriktad ANOVA |
| Två grupper, upprepade åtgärder | Parat t-test | Wilcoxon matchade par signerade rangtest |
| Fler än två grupper, upprepade åtgärder | Envägs, upprepade mätningar ANOVA | Friedmans tvåvägsanalys av varians |
Slutsats
Hypotesundersökning är avgörande för att utvärdera påståenden om populationsparametrar med hjälp av provdata. Parametriska tester förlitar sig på specifika antaganden och är lämpliga för intervall- eller förhållandedata, medan icke-parametriska tester är mer flexibla och applicerbara på nominella eller ordinaldata utan strikta fördelningsantaganden. Tester som Shapiro-Wilk och Anderson-Darling bedömer normaliteten, medan Chi-square och Jarque-Bera utvärderar god passform. Att förstå skillnaderna mellan parametriska och icke-parametriska test är avgörande för att välja lämplig statistisk metod. Sammantaget ger hypotestestning ett systematiskt ramverk för att fatta datadrivna beslut och dra tillförlitliga slutsatser från empiriska bevis.
Är du redo att bemästra avancerad statistisk analys? Anmäl dig till vår BlackBelt Data Analysis-kurs idag! Få expertis inom hypotestestning, parametriska och icke-parametriska tester, Python-implementering och mer. Lyft dina statistiska färdigheter och briljera i datadrivet beslutsfattande. Gå med nu!
Vanliga frågor
A. Parametriska tester gör antaganden om populationsfördelning och parametrar, såsom normalitet och varianshomogenitet, medan icke-parametriska test inte förlitar sig på dessa antaganden. Parametriska tester har mer kraft när antaganden är uppfyllda, medan icke-parametriska tester är mer robusta och tillämpbara i ett större antal situationer, inklusive när data är skeva eller inte normalfördelade.
A. Chi-kvadrattestet används för att fastställa om det finns ett signifikant samband mellan två kategoriska variabler. Den analyserar vanligen kategoriska data och testar hypoteser om variablers oberoende i beredskapstabeller.
A. Mann-Whitney U-testet jämför två oberoende grupper när den beroende variabeln är ordinal eller inte normalfördelad. Den bedömer om det finns en signifikant skillnad mellan medianerna för de två grupperna.
S. Shapiro-Wilk-testet bedömer om ett urval kommer från en normalfördelad population. Den testar nollhypotesen att data följer en normalfördelning. Om p-värdet är mindre än den valda signifikansnivån (t.ex. 0.05) förkastar vi nollhypotesen och drar slutsatsen att data inte är normalfördelade.
- SEO-drivet innehåll och PR-distribution. Bli förstärkt idag.
- PlatoData.Network Vertical Generative Ai. Styrka dig själv. Tillgång här.
- PlatoAiStream. Web3 Intelligence. Kunskap förstärkt. Tillgång här.
- Platoesg. Kol, CleanTech, Energi, Miljö, Sol, Avfallshantering. Tillgång här.
- PlatoHealth. Biotech och kliniska prövningar Intelligence. Tillgång här.
- Källa: https://www.analyticsvidhya.com/blog/2024/04/a-comprehensive-guide-on-non-parametric-tests/



