Computerwetenschappers zijn een veeleisend stel. Voor hen is het niet genoeg om het juiste antwoord op een probleem te krijgen; het doel is bijna altijd om het antwoord zo efficiënt mogelijk te krijgen.

Neem de handeling van het vermenigvuldigen van matrices of reeksen getallen. In 1812 bedacht de Franse wiskundige Jacques Philippe Marie Binet de basisset regels die we studenten nog steeds onderwijzen. Het werkt prima, maar andere wiskundigen hebben manieren gevonden om het proces te vereenvoudigen en te versnellen. Nu de taak van het proces versnellen van matrixvermenigvuldiging ligt op het kruispunt van wiskunde en informatica, waar onderzoekers het proces tot op de dag van vandaag blijven verbeteren – hoewel de winst de afgelopen decennia tamelijk bescheiden was. Sinds 1987 zijn de numerieke verbeteringen in de matrixvermenigvuldiging ‘klein en … extreem moeilijk te verkrijgen’, zegt hij François Le Gall, een computerwetenschapper aan de Universiteit van Nagoya.

Nu hebben drie onderzoekers – Ran Duan en Renfei Zhou van Tsinghua University en Hongxun Wu van de University of California, Berkeley – een grote stap voorwaarts gezet in de aanpak van dit eeuwige probleem. Hun nieuwe resultaten, afgelopen november gepresenteerd op de Foundations of Computer Science-conferentie, komt voort uit een onverwachte nieuwe techniek, zei Le Gall. Hoewel de verbetering zelf relatief klein was, noemde Le Gall deze ‘conceptueel groter dan andere voorgaande’.

De techniek onthult een voorheen onbekende en dus onaangeboorde bron van potentiële verbeteringen, en heeft al vruchten afgeworpen: Een tweede papier, gepubliceerd in januari, bouwt voort op de eerste en laat zien hoe matrixvermenigvuldiging nog verder kan worden gestimuleerd.

“Dit is een grote technische doorbraak”, aldus de woordvoerder Willem Kuszmaul, een theoretische computerwetenschapper aan de Harvard University. “Het is de grootste verbetering in matrixvermenigvuldiging die we in meer dan tien jaar hebben gezien.”

Voer de matrix in

Het lijkt misschien een obscuur probleem, maar matrixvermenigvuldiging is een fundamentele computerbewerking. Het is opgenomen in een groot deel van de algoritmen die mensen dagelijks gebruiken voor allerlei taken, van het weergeven van scherpere computergraphics tot het oplossen van logistieke problemen in de netwerktheorie. En net als op andere gebieden van de berekening is snelheid van het grootste belang. Zelfs kleine verbeteringen kunnen uiteindelijk leiden tot aanzienlijke besparingen in tijd, rekenkracht en geld. Maar voorlopig zijn theoretici vooral geïnteresseerd in het uitzoeken hoe snel het proces ooit kan zijn.

De traditionele manier om twee te vermenigvuldigen nPern matrices — door getallen uit elke rij in de eerste matrix te vermenigvuldigen met getallen in de kolommen in de tweede — vereist n³ aparte vermenigvuldigingen. Voor 2-bij-2-matrices betekent dit 2³ of 8 vermenigvuldigingen.

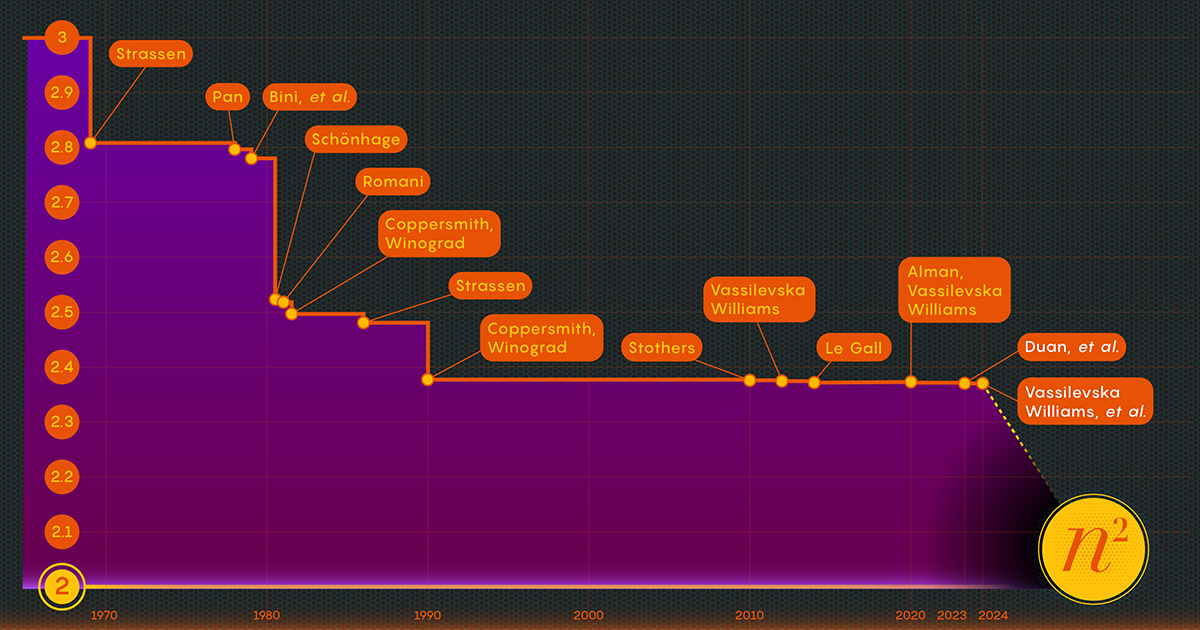
In 1969 onthulde de wiskundige Volker Strassen een ingewikkelder procedure waarmee matrices van 2 bij 2 konden worden vermenigvuldigd in slechts zeven vermenigvuldigingsstappen en 18 optellingen. Twee jaar later demonstreerde computerwetenschapper Shmuel Winograd dat zeven inderdaad het absolute minimum is voor 2-bij-2-matrices.

Strassen exploiteerde datzelfde idee om dat allemaal groter te laten zien nPern matrices kunnen ook worden vermenigvuldigd met minder dan n³ stappen. Een sleutelelement in deze strategie is een procedure die decompositie wordt genoemd: het opsplitsen van een grote matrix in opeenvolgend kleinere submatrices, die uiteindelijk zo klein kunnen zijn als 2 bij 2 of zelfs 1 bij 1 (dit zijn slechts enkele getallen).

De grondgedachte voor het verdelen van een gigantische array in kleine stukjes is volgens Virginia Vassilevska Williams, een computerwetenschapper aan het Massachusetts Institute of Technology en co-auteur van een van de nieuwe artikelen. "Het is moeilijk voor een mens om naar een grote matrix te kijken (bijvoorbeeld in de orde van 100 bij 100) en het best mogelijke algoritme te bedenken", zei Vassilevska Williams. Zelfs 3-bij-3-matrices zijn nog niet volledig opgelost. “Toch kun je een snel algoritme dat je al voor kleine matrices hebt ontwikkeld, gebruiken om ook voor grotere matrices een snel algoritme te verkrijgen.”

De sleutel tot snelheid, zo hebben onderzoekers vastgesteld, is het verminderen van het aantal vermenigvuldigingsstappen, waardoor die exponent wordt verlaagd n³ (voor de standaardmethode) zoveel mogelijk. De laagst mogelijke waarde, n², is eigenlijk net zo lang als het duurt om het antwoord op te schrijven. Computerwetenschappers noemen die exponent omega, ω, met n^ω zijnde de minste mogelijke stappen die nodig zijn om twee met succes te vermenigvuldigen nPern matrixen als n wordt erg groot. “Het punt van dit werk,” zei Zhou, die ook co-auteur was van het artikel van januari 2024, “is om te zien hoe dicht je bij 2 kunt komen, en of dit in theorie haalbaar is.”

Een laserfocus

In 1986 beleefde Strassen opnieuw een grote doorbraak toen hij geïntroduceerd wat de lasermethode voor matrixvermenigvuldiging wordt genoemd. Strassen gebruikte het om een ​​bovenwaarde voor omega van 2.48 vast te stellen. Hoewel de methode slechts één stap is in grote matrixvermenigvuldigingen, is het een van de belangrijkste omdat onderzoekers deze blijven verbeteren.

Een jaar later introduceerden Winograd en Don Coppersmith een nieuw algoritme dat de lasermethode prachtig aanvulde. Deze combinatie van hulpmiddelen heeft een rol gespeeld in vrijwel alle daaropvolgende pogingen om de matrixvermenigvuldiging te versnellen.

Hier is een vereenvoudigde manier om na te denken over hoe deze verschillende elementen in elkaar passen. Laten we beginnen met twee grote matrices, A en B, die u met elkaar wilt vermenigvuldigen. Eerst ontbind je ze in veel kleinere submatrices, of blokken, zoals ze soms worden genoemd. Vervolgens kun je het algoritme van Coppersmith en Winograd gebruiken als een soort handleiding voor het hanteren en uiteindelijk assembleren van de blokken. “Het vertelt me ​​wat ik moet vermenigvuldigen en wat ik moet toevoegen en welke gegevens waar naartoe moeten” in de productmatrix C, zei Vassilevska Williams. “Het is gewoon een recept om C op te bouwen uit A en B.”

Er zit echter een addertje onder het gras: soms krijg je blokken die gemeenschappelijke vermeldingen hebben. Als u deze in het product laat staan, komt dit neer op het tweemaal tellen van deze vermeldingen, dus op een gegeven moment moet u zich ontdoen van die dubbele termen, die overlappingen worden genoemd. Onderzoekers doen dit door de blokken waarin ze zich bevinden te ‘doden’ – door hun componenten gelijk te stellen aan nul om ze uit de berekening te verwijderen.

Dat is waar de lasermethode van Strassen eindelijk in het spel komt. "De lasermethode werkt doorgaans heel goed en vindt over het algemeen een goede manier om een ​​subset van blokken te vernietigen om de overlap te verwijderen", aldus Le Gall. Nadat de laser alle overlappingen heeft geëlimineerd of ‘weggebrand’, kunt u de uiteindelijke productmatrix samenstellen, C.

Het samenvoegen van deze verschillende technieken resulteert in een algoritme voor het vermenigvuldigen van twee matrices met een opzettelijk gierig aantal vermenigvuldigingen in het algemeen – althans in theorie. De lasermethode is niet praktisch bedoeld; het is gewoon een manier om na te denken over de ideale manier om matrices te vermenigvuldigen. "We voeren de methode nooit uit [op een computer]", zei Zhou. “Wij analyseren het.”

En die analyse heeft geleid tot de grootste verbetering van omega in meer dan tien jaar.

Er is een verlies gevonden

Uit het artikel van Duan, Zhou en Wu van afgelopen zomer bleek dat het proces van Strassen nog aanzienlijk versneld kon worden. Het kwam allemaal door een concept dat ze een verborgen verlies noemden, diep verborgen in eerdere analyses – “een gevolg van het onbedoeld doden van te veel blokken”, zei Zhou.

De lasermethode werkt door blokken met overlappingen te labelen als afval, bestemd voor verwijdering; andere blokken worden als waardig beschouwd en worden opgeslagen. Het selectieproces is echter enigszins gerandomiseerd. Een blok dat als afval wordt beoordeeld, kan in feite toch nuttig blijken te zijn. Dit was geen totale verrassing, maar door veel van deze willekeurige keuzes te onderzoeken, stelde het team van Duan vast dat de lasermethode blokken systematisch onderwaardeerde: er zouden meer blokken moeten worden opgeslagen en minder weggegooid. En, zoals meestal het geval is, vertaalt minder verspilling zich in grotere efficiëntie.

"Het kunnen behouden van meer blokken zonder overlap leidt dus tot een sneller algoritme voor matrixvermenigvuldiging", aldus Le Gall.

Nadat het team van Duan het bestaan ​​van dit verlies had bewezen, wijzigde het de manier waarop de lasermethode blokken labelde, waardoor de hoeveelheid afval aanzienlijk werd verminderd. Als gevolg hiervan hebben ze een nieuwe bovengrens voor omega vastgesteld op ongeveer 2.371866 – een verbetering ten opzichte van de vorige bovengrens van 2.3728596. ingesteld in 2020 door Josh Alman en Vassilevska Williams. Dat lijkt misschien een bescheiden verandering, waarbij de grens met ongeveer 0.001 wordt verlaagd. Maar het is de grootste verbetering die wetenschappers sinds 2010 hebben gezien. Het resultaat van Vassilevska Williams en Alman voor 2020 verbeterde in vergelijking met zijn voorganger slechts 0.00001.

Maar wat het meest opwindend is voor onderzoekers is niet alleen het nieuwe record zelf – dat niet lang stand hield. Het is ook het feit dat de krant een nieuwe weg voor verbetering onthulde die tot dan toe totaal onopgemerkt was gebleven. Al bijna vier decennia vertrouwt iedereen op dezelfde lasermethode, zei Le Gall. "Toen ontdekten ze dat we het beter kunnen doen."

Het artikel uit januari 2024 verfijnde deze nieuwe aanpak, waardoor Vassilevska Williams, Zhou en hun co-auteurs het verborgen verlies verder konden verminderen. Dit leidde tot een extra verbetering van de bovengrens van omega, waardoor deze werd teruggebracht tot 2.371552. De auteurs hebben dezelfde techniek ook gegeneraliseerd om het vermenigvuldigingsproces voor rechthoekige (nPerm) matrices — een procedure die toepassingen heeft in de grafentheorie, machinaal leren en andere gebieden.

Enige verdere vooruitgang in deze richting is vrijwel zeker, maar er zijn grenzen. In 2015 Le Gall en twee medewerkers bewezen dat de huidige aanpak – de lasermethode gekoppeld aan het Coppersmith-Winograd-recept – geen omega onder 2.3078 kan opleveren. Om verdere verbeteringen aan te brengen, zei Le Gall, “moet je de oorspronkelijke [aanpak] van Coppersmith en Winograd verbeteren, die sinds 1987 niet echt is veranderd.. ' Maar tot nu toe heeft niemand een betere manier bedacht. Misschien is er niet eens één.

“Het verbeteren van omega is eigenlijk onderdeel van het begrijpen van dit probleem,” zei Zhou. “Als we het probleem goed kunnen begrijpen, kunnen we er betere algoritmen voor ontwerpen. [En] mensen bevinden zich nog in de allereerste fase van het begrijpen van dit eeuwenoude probleem.”