컴퓨터 과학자들은 까다로운 사람들입니다. 그들에게는 문제에 대한 올바른 답을 얻는 것만으로는 충분하지 않습니다. 거의 항상 목표는 가능한 한 효율적으로 답을 얻는 것입니다.

행렬이나 숫자 배열을 곱하는 행위를 해보세요. 1812년에 프랑스 수학자 자크 필립 마리 비네(Jacques Philippe Marie Binet)는 우리가 여전히 학생들에게 가르치고 있는 기본 규칙 세트를 고안했습니다. 이는 완벽하게 작동하지만 다른 수학자들은 프로세스를 단순화하고 속도를 높이는 방법을 찾았습니다. 이제 과제는 프로세스를 가속화 행렬 곱셈은 수학과 컴퓨터 과학의 교차점에 있으며, 연구자들은 오늘날까지 계속해서 프로세스를 개선하고 있습니다. 하지만 최근 수십 년 동안 그 성과는 상당히 미미했습니다. 1987년 이후 행렬 곱셈의 수치적 개선은 "작고... 얻기가 극도로 어려웠습니다"라고 말했습니다. 프랑수아 르 갈, 나고야 대학의 컴퓨터 과학자.

이제 세 명의 연구원(Tsinghua University의 Ran Duan과 Renfei Zhou, 캘리포니아 버클리 대학의 Hongxun Wu)은 이 고질적인 문제를 해결하는 데 큰 진전을 이루었습니다. 그들의 새로운 결과작년 11월 Foundations of Computer Science 컨퍼런스에서 발표된 는 예상치 못한 새로운 기술에서 비롯되었다고 Le Gall은 말했습니다. 개선 자체는 상대적으로 작았지만 르 갈은 “개념적으로는 이전의 다른 개선 사항보다 크다”고 평가했습니다.

이 기술은 이전에 알려지지 않았으므로 아직 개발되지 않은 잠재적인 개선의 원천을 밝혀냈으며 이미 결실을 맺었습니다. 두 번째 논문1월에 출판된 는 행렬 곱셈을 더욱 향상시킬 수 있는 방법을 보여주는 첫 번째 책을 기반으로 합니다.

“이것은 중대한 기술적 혁신이다”라고 그는 말했다. 윌리엄 쿠스마울, 하버드 대학의 이론 컴퓨터 과학자입니다. "이것은 지난 10년 동안 우리가 본 행렬 곱셈의 가장 큰 개선입니다."

매트릭스 입력

모호한 문제처럼 보일 수도 있지만 행렬 곱셈은 기본적인 계산 작업입니다. 이는 보다 선명한 컴퓨터 그래픽 표시부터 네트워크 이론의 물류 문제 해결에 이르기까지 다양한 작업에 사람들이 매일 사용하는 알고리즘의 상당 부분에 통합되어 있습니다. 그리고 다른 계산 영역과 마찬가지로 속도가 가장 중요합니다. 약간의 개선이라도 결국에는 시간, 계산 능력 및 비용을 크게 절약할 수 있습니다. 그러나 현재 이론가들은 주로 프로세스가 얼마나 빨라질 수 있는지 알아내는 데 관심이 있습니다.

2를 곱하는 전통적인 방법 n-으로-n 행렬 — 첫 번째 행렬의 각 행에 있는 숫자와 두 번째 행렬의 열에 있는 숫자를 곱하여 — 필요 n³ 별도의 곱셈. 2x2 행렬의 경우 이는 2를 의미합니다.³ 또는 8번 곱셈.

1969년 수학자 폴커 스트라센(Volker Strassen)은 단 2번의 곱셈 단계와 2번의 덧셈만으로 18x2 행렬을 곱할 수 있는 더 복잡한 절차를 공개했습니다. 2년 후, 컴퓨터 과학자 Shmuel Winograd는 XNUMX이 실제로 XNUMXxXNUMX 행렬의 절대 최소값임을 입증했습니다.

Strassen은 동일한 아이디어를 활용하여 모든 것이 더 크다는 것을 보여주었습니다. n-으로-n 행렬은 또한 n³ 단계. 이 전략의 핵심 요소에는 분해라는 절차가 포함됩니다. 즉, 큰 행렬을 연속적으로 작은 부분행렬로 분해하여 결국 2x2 또는 심지어 1x1(단지 단일 숫자임)만큼 작아질 수 있습니다.

거대한 배열을 작은 조각으로 나누는 이유는 매우 간단합니다. 버지니아 바실 레프 스카 윌리엄스, MIT의 컴퓨터 과학자이자 새로운 논문 중 하나의 공동 저자입니다. Vassilevska Williams는 "인간이 큰 행렬(예: 100x100 정도)을 보고 가능한 최상의 알고리즘을 생각하는 것은 어렵습니다."라고 말했습니다. 3x3 행렬도 아직 완전히 풀리지 않았습니다. 그럼에도 불구하고 작은 행렬을 위해 이미 개발한 빠른 알고리즘을 사용하여 더 큰 행렬을 위한 빠른 알고리즘을 얻을 수도 있습니다.

연구원들이 판단한 속도의 핵심은 곱셈 단계 수를 줄여 해당 지수를 낮추는 것입니다. n³ (표준 방법의 경우) 가능한 한 많이. 가능한 가장 낮은 값, n², 기본적으로 답변을 작성하는 데 걸리는 시간입니다. 컴퓨터 과학자들은 이 지수를 오메가(Ω)라고 부릅니다. n^ω 두 개를 성공적으로 곱하는 데 필요한 최소한의 단계입니다. n-으로-n 행렬 n 매우 크게 자랍니다. 2024년 2월 논문의 공동 집필자인 Zhou는 "이 연구의 요점은 XNUMX에 얼마나 가까워질 수 있는지, 그리고 그것이 이론적으로 달성될 수 있는지 확인하는 것"이라고 말했습니다.

레이저 초점

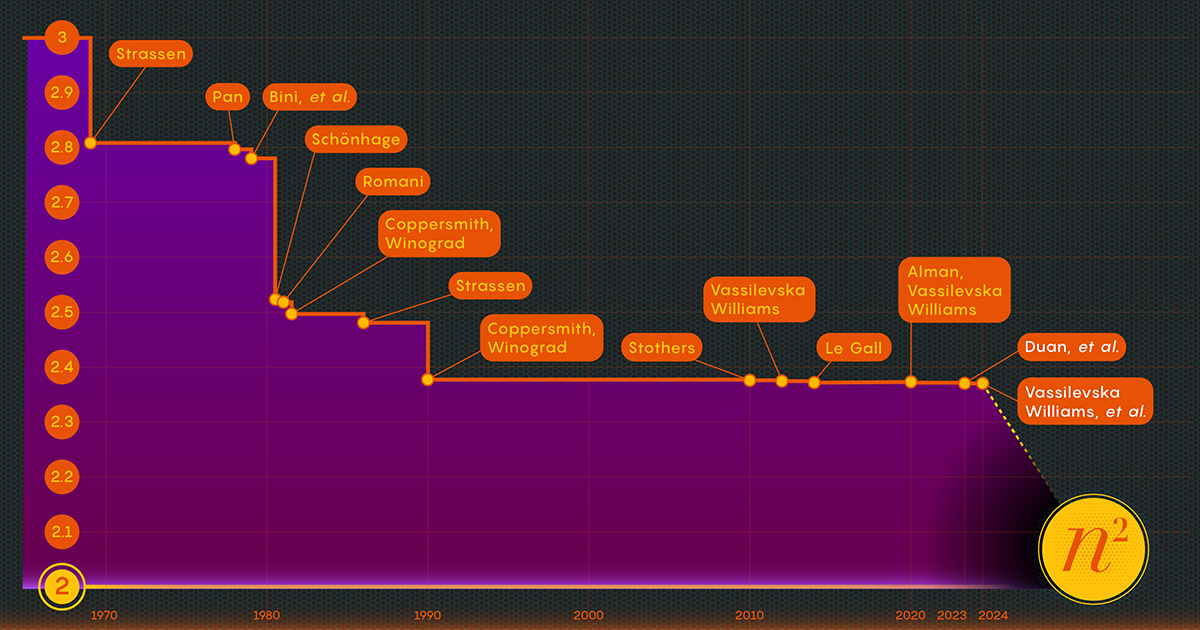
1986년 Strassen은 또 다른 큰 돌파구를 마련했습니다. 소개 행렬 곱셈을 위한 레이저 방법이라고 불리는 것이 있습니다. Strassen은 이를 사용하여 오메가의 상한값인 2.48을 설정했습니다. 이 방법은 대규모 행렬 곱셈의 한 단계일 뿐이지만 연구자들이 계속해서 개선해 왔기 때문에 가장 중요한 방법 중 하나입니다.

1년 후, Winograd와 Don Coppersmith는 레이저 방법을 아름답게 보완하는 새로운 알고리즘을 도입했습니다. 이러한 도구 조합은 행렬 곱셈 속도를 높이기 위한 사실상 모든 후속 노력에 사용되었습니다.

이러한 다양한 요소가 어떻게 결합되는지에 대한 단순화된 생각은 다음과 같습니다. 함께 곱하려는 두 개의 큰 행렬 A와 B부터 시작하겠습니다. 먼저 이를 때때로 호출되는 여러 개의 작은 하위 행렬 또는 블록으로 분해합니다. 다음으로, Coppersmith와 Winograd의 알고리즘을 사용하여 블록을 처리하고 최종적으로 조립하기 위한 일종의 지침 매뉴얼 역할을 할 수 있습니다. Vassilevska Williams는 제품 매트릭스 C에서 "무엇을 곱하고 무엇을 추가해야 하며 어떤 항목이 어디로 가는지 알려줍니다"라고 말했습니다. "이것은 A와 B에서 C를 구성하는 레시피일 뿐입니다."

그러나 문제가 있습니다. 공통 항목이 있는 블록으로 끝나는 경우가 있습니다. 이를 제품에 남겨 두는 것은 해당 항목을 두 번 계산하는 것과 유사하므로 어느 시점에서는 중복이라고 하는 중복된 용어를 제거해야 합니다. 연구자들은 자신이 속한 블록을 "삭제"하여 이를 수행합니다. 즉, 해당 구성 요소를 0으로 설정하여 계산에서 제거합니다.

Strassen의 레이저 방법이 마침내 작동하게 되는 곳입니다. "레이저 방법은 일반적으로 매우 잘 작동하며 일반적으로 중복을 제거하기 위해 블록의 하위 집합을 죽이는 좋은 방법을 찾습니다."라고 Le Gall은 말했습니다. 레이저가 모든 겹침을 제거하거나 "소각"한 후 최종 제품 매트릭스 C를 구성할 수 있습니다.

이러한 다양한 기술을 결합하면 적어도 이론적으로는 전체적으로 고의적으로 인색한 수의 곱셈을 사용하여 두 행렬을 곱하는 알고리즘이 생성됩니다. 레이저 방법은 실용적이지 않습니다. 이는 행렬을 곱하는 이상적인 방법을 생각하는 방법일 뿐입니다. Zhou는 “우리는 [컴퓨터에서] 이 방법을 실행하지 않습니다. “우리는 그것을 분석합니다.”

그리고 그 분석은 지난 10여년 동안 오메가의 가장 큰 개선으로 이어졌습니다.

손실이 발견되었습니다

지난 여름 Duan, Zhou 및 Wu가 작성한 논문에서는 Strassen의 프로세스가 여전히 상당히 가속화될 수 있음을 보여주었습니다. 이는 모두 이전 분석에 깊이 묻혀 있던 숨겨진 손실이라는 개념 때문이었습니다. "의도치 않게 너무 많은 블록을 죽인 결과"라고 Zhou는 말했습니다.

레이저 방법은 겹쳐진 블록을 쓰레기로 분류하여 폐기하도록 지정하는 방식으로 작동합니다. 다른 블록은 가치 있는 것으로 간주되어 저장됩니다. 그러나 선택 과정은 다소 무작위입니다. 쓰레기로 평가된 블록은 실제로 결국 유용한 것으로 판명될 수 있습니다. 이것은 전혀 놀라운 일이 아니었지만 이러한 무작위 선택 중 다수를 조사함으로써 Duan의 팀은 레이저 방법이 체계적으로 블록의 가치를 과소평가하고 있다고 판단했습니다. 즉, 더 많은 블록을 저장하고 더 적은 수의 블록을 버려야 합니다. 그리고 일반적으로 그렇듯이 낭비가 적을수록 효율성이 높아집니다.

Le Gall은 “겹침 없이 더 많은 블록을 유지할 수 있으면 더 빠른 행렬 곱셈 알고리즘이 가능해집니다.”라고 말했습니다.

이러한 손실의 존재를 입증한 후 Duan의 팀은 레이저 방법으로 블록을 라벨링하는 방식을 수정하여 폐기물을 크게 줄였습니다. 결과적으로 그들은 오메가의 새로운 상한선을 약 2.371866으로 설정했습니다. 이는 이전 상한선인 2.3728596보다 개선된 수치입니다. 2020 년을 배경으로 Josh Alman과 Vassilevska Williams의 작품입니다. 이는 경계를 약 0.001만큼 낮추는 작은 변화처럼 보일 수 있습니다. 그러나 이는 2010년 이후 과학자들이 본 가장 큰 개선 사항입니다. Vassilevska Williams와 Alman의 2020년 결과는 이에 비해 이전 버전보다 0.00001만 개선되었습니다.

그러나 연구자에게 가장 흥미로운 것은 오래 가지 못한 새로운 기록 그 자체만이 아닙니다. 또한 이 논문은 그때까지 전혀 눈에 띄지 않았던 개선을 위한 새로운 길을 밝혀냈다는 사실이기도 합니다. 거의 40년 동안 모든 사람들이 동일한 레이저 방법을 사용해 왔다고 Le Gall은 말했습니다. "그런 다음 그들은 우리가 더 잘할 수 있다는 것을 발견했습니다."

2024년 2.371552월 논문에서는 이 새로운 접근 방식을 개선하여 Vassilevska Williams, Zhou 및 공동 저자가 숨겨진 손실을 더욱 줄일 수 있도록 했습니다. 이로 인해 오메가의 상한이 추가로 개선되어 XNUMX로 감소되었습니다. 저자는 또한 직사각형의 곱셈 과정을 개선하기 위해 동일한 기술을 일반화했습니다(n-으로-m) 행렬 — 그래프 이론, 기계 학습 및 기타 분야에 적용되는 절차입니다.

이러한 측면에서 추가적인 진전은 거의 확실하지만 한계가 있습니다. 2015년에는 르 갈과 두 명의 협력자가 증명 현재 접근 방식(Coppersmith-Winograd 레시피와 결합된 레이저 방법)은 2.3078 미만의 오메가를 생성할 수 없습니다. Le Gall은 추가 개선을 위해서는 “1987년 이후 실제로 변하지 않은 Coppersmith 및 Winograd의 원래 [접근 방식]을 개선해야 합니다.. " 그러나 지금까지 아무도 더 나은 방법을 찾지 못했습니다. 심지어 하나도 없을 수도 있습니다.

“오메가를 개선하는 것은 실제로 이 문제를 이해하는 것의 일부입니다.”라고 Zhou는 말했습니다. “문제를 잘 이해할 수 있다면 더 나은 알고리즘을 설계할 수 있습니다. [그리고] 사람들은 아직 이 오래된 문제를 이해하는 초기 단계에 있습니다.”