개요
이번 글에서는 무엇이 무엇인지 알아보겠습니다. 가설 검증, 귀무가설과 대립가설의 공식화, 가설 테스트 설정에 중점을 두고 모수적 테스트와 비모수적 테스트에 대해 자세히 알아보고 각각의 가정과 Python에서의 구현을 논의합니다. 그러나 우리의 주요 초점은 Mann-Whitney U 테스트 및 Kruskal-Wallis 테스트와 같은 비모수적 테스트에 있습니다. 마지막에는 가설 검정에 대한 포괄적인 이해와 이러한 개념을 자신의 통계 분석에 적용할 수 있는 실용적인 도구를 갖추게 됩니다.
학습 목표
- 귀무 가설과 대립 가설의 수립을 포함하여 가설 검정의 원리를 이해합니다.
- 가설 검정 설정.
- Parametric Test 및 그 종류에 대한 이해
- 비모수적 테스트와 그 유형 및 구현에 대해 이해합니다.
- 파라메트릭과 비파라메트릭의 차이점
차례
가설 테스트란 무엇입니까?
가설은 개인/조직이 주장하는 것입니다. 주장은 일반적으로 평균이나 비율과 같은 모집단 매개변수에 관한 것이며 우리는 주장을 뒷받침하는 증거를 표본에서 찾습니다.
유의성 테스트라고도 하는 가설 테스트는 표본에서 측정된 데이터를 사용하여 모집단의 매개변수에 대한 주장이나 가설을 확인하는 방법입니다. 이 방법을 사용하여 모집단 모수 가설이 참이었다면 표본 통계가 선택되었을 가능성을 결정하여 여러 이론을 탐색합니다.
가설 테스트에는 두 가지 가설의 공식화가 포함됩니다.
- 귀무가설(H0)
- 대립가설(H1)
귀무 가설 : 이는 일반적으로 차이가 없다는 가설이며 일반적으로 H0로 표시됩니다. RA Fisher에 따르면 귀무 가설은 그것이 참이라는 가정 하에서 기각 가능성을 테스트하는 가설입니다(Ref Fundamentals of Mathematical Statistics).
대립 가설: 귀무가설을 보완하는 모든 가설을 대립가설이라고 하며 일반적으로 H1로 표시합니다.
가설 검정의 목적은 귀무 가설을 기각하거나 유지하여 두 변수(보통 독립 변수 하나와 종속 변수 하나, 즉 하나는 원인이고 다른 하나는 결과) 사이에 통계적으로 유의미한 관계를 설정하는 것입니다.
가설 검정 설정
- 가설을 말로 설명하거나 주장하십시오.
- 주장에 기초하여 귀무가설과 대립가설을 정의합니다.
- 위 주장에 적합한 가설 검정 유형을 식별하십시오.
- 귀무가설의 타당성을 검정하는 데 사용할 검정 통계량을 식별합니다.
- 귀무가설의 기각 및 유지 기준을 결정합니다. 이를 전통적으로 α(알파) 기호로 표시하는 유의성 값이라고 합니다.
- 귀무가설이 참일 때 검정 통계값을 관찰할 조건부 확률인 p-값을 계산합니다. 간단히 말해서, p-값은 귀무 가설을 뒷받침하는 증거입니다.
파라메트릭 및 비파라메트릭 테스트
비모수적 통계 테스트는 데이터가 샘플링되는 모집단 분포의 모수에 대한 가정에 의존하지 않는 반면, 모수적 통계 테스트는 그렇지 않습니다.
파라메트릭 테스트
대부분의 통계 테스트는 일련의 가정을 기반으로 수행됩니다. 특정 가정이 위반되면 분석에서 오해의 소지가 있거나 완전히 잘못된 결론이 나올 수 있습니다.
일반적으로 가정은 다음과 같습니다.
- 정규성: 테스트할 매개변수의 샘플링 분포는 정규(또는 적어도 대칭) 분포를 따릅니다.
- 분산의 동질성: 두 개의 서로 다른 모집단에서 나오는 모집단 평균을 테스트하지 않는 한 데이터의 분산은 서로 다른 그룹에서 동일합니다.
파라메트릭 테스트 중 일부는 다음과 같습니다.
- Z-테스트: 모집단 표준 편차가 알려진 경우 모집단 평균, 분산 또는 비율을 검정합니다.
- 학생의 t-테스트: 모집단 표준 편차를 알 수 없는 경우 모집단 평균, 분산 또는 비율을 검정합니다.
- 쌍체 t-검정: 관련된 두 그룹 또는 조건의 평균을 비교하는 데 사용됩니다.
- 분산 분석(ANOVA): 3개 이상의 독립 그룹에 걸쳐 평균을 비교하는 데 사용됩니다.
- 회귀 분석: 하나 이상의 독립변수와 종속변수 사이의 관계를 평가하는 데 사용됩니다.
- 공분산 분석(ANCOVA): 추가 공변량을 분석에 통합하여 ANOVA를 확장합니다.
- 다변량 분산 분석(MANOVA): 그룹 간 여러 종속 변수의 차이를 평가하기 위해 ANOVA를 확장합니다.
이제 비모수적 테스트에 대해 자세히 살펴보겠습니다.
비모수적 테스트
울포위츠는 1942년에 처음으로 "비모수적"이라는 용어를 사용했습니다. 비모수적 통계의 개념을 이해하려면 먼저 방금 논의한 모수적 통계에 대한 기본적인 이해가 있어야 합니다. ㅏ 파라메트릭 테스트 특정 분포(보통 정규 분포)를 따르는 표본이 필요합니다. 또한 비모수적 테스트는 정규성과 같은 모수적 가정과 무관합니다.
비모수적 테스트(모집단 분포에 대한 가정이 없기 때문에 분포 자유 테스트라고도 함). 비모수적 테스트는 테스트가 데이터가 다음에서 추출되었다는 가정을 기반으로 하지 않음을 의미합니다. 확률 분포 평균, 비율, 표준편차 등의 매개변수를 통해 정의됩니다.
비모수적 테스트는 다음 중 하나에 사용됩니다.
- 이 테스트는 평균이나 비율과 같은 모집단 매개변수에 관한 것이 아닙니다.
- 이 방법에는 모집단 분포에 대한 가정(예: 모집단이 정규 분포를 따른다)이 필요하지 않습니다.
비모수적 테스트 유형
이제 Chi-Square 테스트, Mann-Whitney 테스트, Wilcoxon Signed Rank 테스트 및 Kruskal-Wallis 테스트를 수행하는 개념과 절차에 대해 논의해 보겠습니다.
카이-제곱 테스트
두 질적 변수 사이의 연관성이 통계적으로 유의한지 여부를 확인하려면 카이제곱 검정이라는 유의성 검정을 수행해야 합니다.
카이제곱 검정에는 두 가지 주요 유형이 있습니다.
카이제곱 적합도
알 수 없는 분포를 가진 모집단이 알려진 분포에 "적합"하는지 여부를 결정하려면 적합도 검정을 사용합니다. 이 경우 단일 정성적 설문조사 질문이 있거나 단일 모집단의 단일 실험 결과가 있습니다. 적합도는 일반적으로 모집단이 균일한지(모든 결과가 동일한 빈도로 발생함), 모집단이 정규인지, 모집단이 알려진 분포를 갖는 다른 모집단과 동일한지 확인하는 데 사용됩니다. 귀무가설과 대립가설은 다음과 같습니다.
- H0: 모집단이 주어진 분포에 적합합니다.
- Ha: 모집단이 주어진 분포에 맞지 않습니다.
예를 들어 이것을 이해해보자
| 낮 | 월요일 | 화요일 | 수요일 | 목요일 | 금요일 | 토요일 | 일요일 |
| 고장 횟수 | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
표에는 요인의 분석 수가 표시됩니다. 이 예에는 단일 변수만 있으며 관찰된 분포(표에 나와 있음)가 예상 분포에 맞는지 여부를 결정해야 합니다.
이를 위해 귀무가설과 대립가설은 다음과 같이 공식화됩니다.
- H0:내역이 균일하게 분포됩니다.
- Ha: 고장이 균일하게 분포되지 않습니다.
그리고 자유도는 n-1이 됩니다(이 경우 n=7, 따라서 df = 7-1=6).
Expected value will be= (14+22+16+18+12+19+11)/7=16
| 낮 | 월요일 | 화요일 | 수요일 | 목요일 | 금요일 | 토요일 | 일요일 |
| 고장 횟수(관찰) | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
| 기대하는 | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| (관찰-예상) | -2 | 6 | 0 | 2 | -4 | 3 | -5 |
| (관찰-예상)^2 | 4 | 36 | 0 | 4 | 16 | 9 | 25 |
이 공식을 사용하여 카이제곱을 계산합니다.
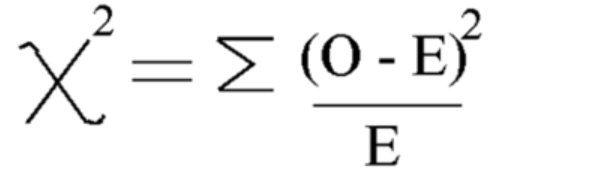
카이제곱 = 5.875
그리고 자유도는 = n-1=7-1=6 입니다.
이제 임계값을 살펴보겠습니다. 카이제곱 분포표 5% 유의수준에서
따라서 임계값은 12.592입니다.
카이제곱 계산값이 임계값보다 작으므로 귀무가설을 채택하고 분석이 균일하게 분포되어 있다는 결론을 내릴 수 있습니다.
카이제곱 검정의 독립성
독립성 검정을 사용하여 두 변수(요인)가 독립인지 종속인지, 즉 이 두 변수가 그들 사이에 유의미한 연관 관계를 가지고 있는지 여부를 결정합니다. 이 경우 두 개의 정성적 설문조사 질문 또는 실험이 있으며 분할표가 구성됩니다. 목표는 두 변수가 관련이 없는지(독립) 또는 관련이 있는지(종속) 확인하는 것입니다. 귀무가설과 대립가설은 다음과 같습니다.
- H0: 두 변수(요인)는 독립적입니다.
- Ha: 두 변수(요인)는 종속적입니다.
예를 들어보자
성별과 선호하는 셔츠 색상이 독립적인지 조사하려는 예입니다. 이는 사람의 성별이 색상 선택에 영향을 미치는지 알아보고 싶다는 의미입니다. 설문조사를 실시하고 데이터를 표로 정리했습니다.
이 표는 관찰된 값입니다.
| 검정 | 백 | 빨간색 | 파란색 | |
| 남성 | 48 | 12 | 33 | 57 |
| 여성 | 34 | 46 | 42 | 26 |
이제 먼저 귀무가설과 대립가설을 공식화합니다.
- H0: 성별, 선호하는 셔츠 색상은 독립적입니다.
- Ha: 성별과 선호하는 셔츠 색상은 독립적이지 않습니다.
카이제곱 검정 통계량을 계산하려면 기대값을 계산해야 합니다. 따라서 모든 행과 열 및 전체 합계를 추가합니다.
| 검정 | 백 | 빨간색 | 파란색 | 금액 | |
| 남성 | 48 | 12 | 33 | 57 | 150 |
| 여성 | 34 | 46 | 42 | 26 | 148 |
| 금액 | 82 | 58 | 75 | 83 | 298 |
그런 다음 이 공식 = (행 합계 * 열 합계)/전체 합계를 사용하여 위 표에서 각 항목에 대한 기대 값 표를 계산할 수 있습니다.
기대값 표:
| 검정 | 백 | 빨간색 | 파란색 | |
| 남성 | 41.3 | 29.2 | 37.8 | 41.8 |
| 여성 | 40.7 | 28.8 | 37.2 | 41.2 |
이제 카이제곱 검정 공식을 사용하여 카이제곱 값을 계산합니다.
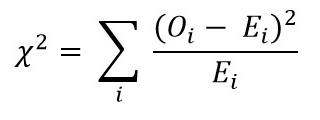
- Oi = 관찰된 값
- Ei = 기대값
우리가 얻는 값은 다음과 같습니다: Χ2 = 34.9572
자유도 계산
DF=(행수-1)*(열수-1)
이제 임계값을 찾아 카이제곱 검정과 비교해 보세요. 통계값:
이를 수행하려면 다음에서 자유도와 유의 수준(알파)을 찾아볼 수 있습니다. 카이제곱 분포표
알파 =0.050에서 임계값 = 7.815를 얻습니다.
카이제곱> 임계값이므로
따라서 우리는 귀무 가설을 기각하고 성별과 선호하는 셔츠 색상이 독립적이지 않다는 결론을 내릴 수 있습니다.
카이제곱 구현
이제 Python의 실제 예제를 사용하여 Chi-Square의 구현을 살펴보겠습니다.
- H0: 성별, 선호하는 셔츠 색상은 독립적입니다.
- Ha: 성별과 선호하는 셔츠 색상은 독립적이지 않습니다.
데이터 세트 생성:
import pandas as pd
from scipy.stats import chi2_contingency
from scipy.stats import chi2
# Given dataset
df_dict = {
'Black': [48, 34],
'White': [12, 46],
'Red': [33, 42],
'Blue': [57, 26]
}
dataset_table = pd.DataFrame(df_dict, index=['Male', 'Female'])
print("Dataset Table:")
print(dataset_table)
print()
# Observed Values
Observed_Values = dataset_table.values
print("Observed Values:")
print(Observed_Values)
print()
# Perform chi-square test
val = chi2_contingency(dataset_table)
Expected_Values = val[3]
print("Expected Values:")
print(Expected_Values)
print()
# Degree of Freedom
no_of_rows = len(dataset_table.iloc[0:2, 0])
no_of_columns = 4
ddof = (no_of_rows - 1) * (no_of_columns - 1)
print("Degree of Freedom:", ddof)
print()
# Chi-square statistic
chi_square = sum([(o - e) ** 2. / e for o, e in zip(Observed_Values, Expected_Values)])
chi_square_statistic = chi_square[0] + chi_square[1]
print("Chi-square statistic:", chi_square_statistic)
print()
# Critical value
alpha = 0.05
critical_value = chi2.ppf(q=1-alpha, df=ddof)
print('Critical value:', critical_value)
print()
# p-value
p_value = 1 - chi2.cdf(x=chi_square_statistic, df=ddof)
print('p-value:', p_value)
print()
# Significance level
print('Significance level:', alpha)
print('p-value:', p_value)
print('Degree of Freedom:', ddof)
print()
# Hypothesis testing
if chi_square_statistic >= critical_value:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
print()
if p_value <= alpha:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
출력:
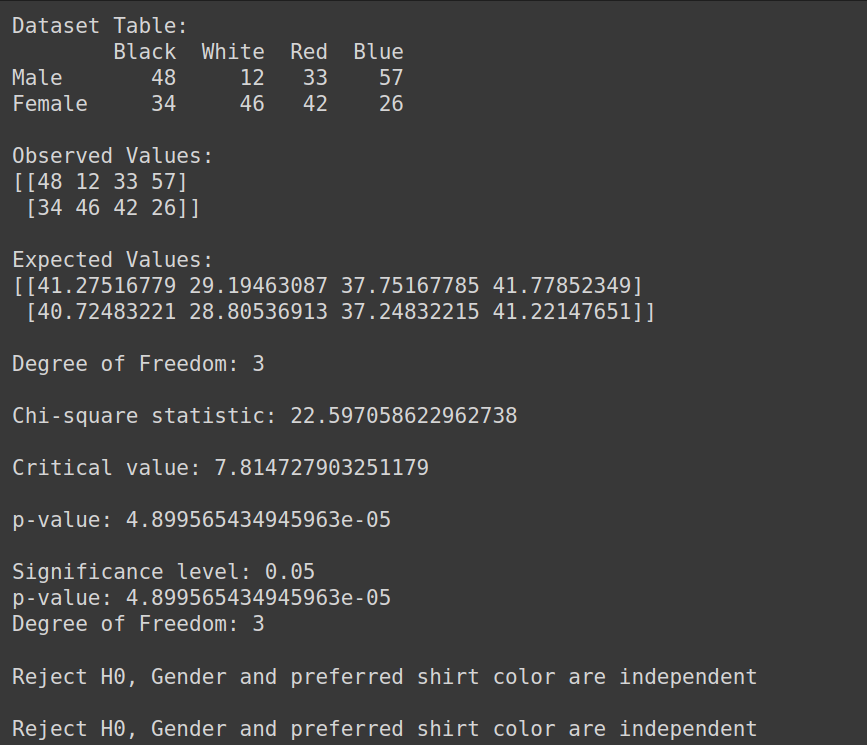
Mann-Whitney U 테스트
Mann-Whitney U 검정은 독립 표본 t 검정에 대한 비모수적 대안으로 사용됩니다. 동일한 모집단의 두 표본 평균을 비교하여 동일한지 확인합니다. 이 검정은 일반적으로 순서형 데이터에 사용되거나 t-검정의 가정이 충족되지 않을 때 사용됩니다.
Mann-Whitney U 테스트는 두 그룹의 모든 값의 순위를 매긴 다음 각 그룹의 순위를 합산합니다. 이러한 순위를 기반으로 검정 통계량 U를 계산합니다. U-통계량은 테이블의 임계값과 비교되거나 근사치를 사용하여 계산됩니다. U-통계량이 임계값보다 작으면 귀무가설이 기각됩니다.
이는 평균을 비교하고 정규 분포를 가정하는 t-테스트와 같은 모수적 테스트와 다릅니다. Mann-Whitney U 검정은 대신 순위를 비교하며 정규 분포 가정이 필요하지 않습니다.
Mann-Whitney U 검정은 결과가 그룹 평균 차이가 아닌 그룹 순위 차이로 표시되므로 이해하기 어려울 수 있습니다.
Mann-Whitney 검정 공식:
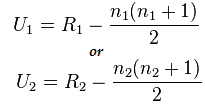
U= 최소(U1,U2)
여기
- U= Mann-Whitney U 테스트
- n1= 표본 크기 XNUMX
- n2= 표본 크기 XNUMX
- R1= 표본 크기 XNUMX의 순위
- R2= 표본 크기 2의 순위
그럼 간단한 예를 통해 이를 이해해 보겠습니다.
환자의 건강 개선에 있어 두 가지 다른 치료 방법(방법 A와 방법 B)의 효과를 비교한다고 가정해 보겠습니다. 우리는 다음과 같은 데이터를 가지고 있습니다:
- 방법 A: 3,4,2,6,2,5
- 방법 B: 9,7,5,10,6,8
여기서는 데이터가 정규 분포를 따르지 않고 표본 크기가 작다는 것을 알 수 있습니다.
Mann-Whitney U 테스트 구현
이제 Mann-Whitney U 테스트를 수행해 보겠습니다.
하지만 먼저 귀무 가설과 대립 가설을 공식화해 보겠습니다.
- H0: 각 시술별 순위에는 차이가 없습니다.
- Ha: 각 시술 별로 순위에 차이가 있습니다.
모든 치료법을 결합하십시오: 3,4,2,6,2,5,9,7,5,10,6,8
정렬된 데이터 : 2,2,3,4,5,5,6,6,7,8,9,10
정렬된 데이터 순위: 1,2,3,4,5,6,7,8,9,10,11,12
- 별도로 데이터 순위 지정:
- Method A: 3(3),4(4),2(1.5),6(7.5),2(1.5),5(5.5)
- Method B: 9(11),7(9),5(5.5),10(12),6(1.5),8(10)
- 순위 합계 계산):
- R1: 3+4+1.5+7.5+1.5+5.5=23
- R2: 11+9+5.5+12+1.5+10=55
이제 다음 공식을 사용하여 통계 값을 계산합니다.
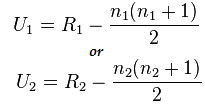
여기서 n1=6이고 n2=6입니다.
그리고 U1=2, U2= 34에 대한 계산 후의 값
U 통계 계산:
우리= 최소(U1,U2)= 최소(2,34)= 2
~ 만-휘트니 테이블 임계값을 찾을 수 있습니다
이 경우 임계 값은 5입니다.
5% 유의수준에서 Uc= 5가 우리보다 크기 때문에 기각합니다. H0
따라서 우리는 각 치료의 순위에 차이가 있다는 결론을 내릴 수 있습니다.
파이썬으로 구현
from scipy.stats import mannwhitneyu, norm
import numpy as np
TreatmentA = np.array([3,4,2,6,2,5])
TreatmentB = np.array([9,7,5,10,6,8])
# Perform Mann-Whitney U test
U_statistic, p_value = mannwhitneyu(TreatmentA, TreatmentB)
# Print the result
print(f'The U-statistic is {U_statistic:.2f} and the p-value is {p_value:.4f}')
if p_value < 0.05:
print("Reject Null Hypothesis: There is a significant difference between the Rank of each treatment.")
else:
print("Fail to Reject Null Hypothesis: Fail to Reject Null Hypothesis: There is no enough evidence to conclude that there is difference between the Rank of each treatment")출력:

크루스칼 – 월리스 테스트
Kruskal –Wallis 테스트는 여러 그룹에 사용됩니다. 이는 정규성과 등분산 가정이 위반되는 경우 일원 분산 분석(one-way ANOVA) 테스트에 대한 비모수적이며 귀중한 대안입니다. Kruskal –Wallis Test는 두 개 이상의 독립 그룹의 중앙값을 비교합니다.
모집단에 대한 정규성 조건을 요구하지 않고 동일한 분포를 갖는 모집단에서 k개의 독립 표본(k>=3)을 추출할 때 귀무 가설을 검정합니다.
가정 :
독립적으로 추출된 무작위 샘플이 5개 이상 있는지 확인하세요. 각 표본에는 최소 5개의 관측치가 있습니다(n>=XNUMX).
세 그룹의 학생이 사용하는 학습 기술이 시험 점수에 영향을 미치는지 확인하려는 예를 생각해 보세요. Kruskal-Wallis 테스트를 사용하여 데이터를 분석하고 그룹 간 시험 점수에 통계적으로 유의미한 차이가 있는지 평가할 수 있습니다.
이에 대한 귀무가설을 다음과 같이 공식화합니다.
- H0: 세 그룹의 학생 간 시험 점수에는 차이가 없습니다.
- Ha: 세 그룹의 학생 사이에 시험 점수에 차이가 있습니다.
Wilcoxon 부호 있는 순위 검정
Wilcoxon 부호 순위 테스트(Wilcoxon 일치 쌍 테스트라고도 함)는 종속 표본 t-검정 또는 쌍체 표본 t-검정의 비모수적 버전입니다. 부호 테스트는 대응 표본 t-테스트에 대한 또 다른 비모수적 대안입니다. 이는 관심 변수가 본질적으로 이분형인 경우(예: 남성과 여성, 예 및 아니오) 사용됩니다. Wilcoxon Signed Rank Test는 단일 표본 t-검정에 대한 비모수적 버전이기도 합니다. Wilcoxon 부호 순위 검정은 두 상황(쌍 표본)에서 그룹의 중앙값을 비교하거나 그룹의 중앙값을 가설 중앙값(1개의 표본)과 비교합니다.
예를 들어 8주 프로그램에 참여하기 전과 후에 흡연자의 일일 담배 소비량에 대한 데이터가 있고 프로그램 전후의 일일 담배 소비량에 유의미한 차이가 있는지 확인하고 싶다고 가정해 보겠습니다. 이 테스트를 사용
이에 대한 가설정립은 다음과 같다.
- H0: 프로그램 전후 일일 담배 소비량에는 차이가 없습니다.
- Ha: 프로그램 전후 일일 담배 소비량에 차이가 있습니다.
정규성 검정
이제 정규성 테스트에 대해 논의하겠습니다.
샤피로 윌크 테스트
Shapiro-Wilk 테스트는 주어진 데이터 샘플이 정규 분포 모집단에서 나온 것인지 여부를 평가합니다. 정규성을 확인하는 데 가장 일반적으로 사용되는 테스트 중 하나입니다. 이 테스트는 상대적으로 작은 표본 크기를 다룰 때 특히 유용합니다.
Shapiro-Wilk 테스트에서:
- 귀무 가설 : 표본 데이터는 정규 분포를 따르는 모집단에서 나옵니다.
- 대체 가설: 표본 데이터는 정규 분포를 따르는 모집단에서 나온 것이 아닙니다.
Shapiro-Wilk 검정에 의해 생성된 검정 통계량은 정규성 가정 하에서 관측된 데이터와 예상 데이터 간의 불일치를 측정합니다. 검정 통계량과 관련된 p-값이 선택한 유의 수준(예: 0.05)보다 작으면 귀무 가설을 기각하여 데이터가 정규 분포를 따르지 않음을 나타냅니다. p-값이 유의 수준보다 크면 귀무 가설을 기각하지 못하므로 데이터가 정규 분포를 따를 수 있음을 나타냅니다.
먼저 이러한 테스트를 위한 데이터 세트를 생성해 보겠습니다. 선택한 데이터 세트를 사용할 수 있습니다.
import pandas as pd
# Create the dictionary with the provided data
data = {
'population': [6.1101, 5.5277, 8.5186, 7.0032, 5.8598],
'profit': [17.5920, 9.1302, 13.6620, 11.8540, 6.8233]
}
# Create the DataFrame
df = pd.DataFrame(data)
response_var=df['profit']
Here, a sample for running Shapiro -Wilk test on python:
from scipy.stats import shapiro
stat, p_val = shapiro(response_var)
print(f'Shapiro-Wilk Test: Statistic={stat} p-value={p_val}')
if p_val > alpha:
print('Data looks normal (fail to reject H0)')
else:
print('Data looks normal (fail to reject H0)')출력:

이 테스트는 표본 크기가 클수록 신뢰성이 떨어지기 때문에 상대적으로 작은 표본 크기(n=< 50-2000)에 가장 적합합니다.
앤더슨-달링
주어진 데이터 샘플이 정규 분포와 같은 지정된 분포에서 나오는지 여부를 평가합니다. Shapiro-Wilk 테스트와 유사하지만 특히 작은 표본 크기에 더 민감합니다.
이는 분포 모수를 알 수 없는 경우 정규 분포를 포함한 여러 분포에 적합합니다.
이를 구현하기 위한 Python 코드는 다음과 같습니다.
from scipy.stats import anderson
response_var = data['profit']
alpha = 0.05
# Anderson-Darling Test
result = anderson(response_var)
print(f'Anderson statistics: {result.statistic:.3f}')
if result.statistic > result.critical_values[-1]:
p_value = 0.0 # The p-value is essentially 0 if the statistic exceeds the largest critical value
else:
p_value = result.significance_level[result.statistic < result.critical_values][-1]
print("P-value:", p_value)
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")출력:

Jarque-Bera 테스트
Jarque-Bera 테스트는 주어진 데이터 샘플이 정규 분포 모집단에서 나온 것인지 여부를 평가합니다. 이는 데이터의 왜도와 첨도를 기반으로 합니다.
다음은 샘플 데이터를 사용하여 Python에서 Jarque-Bera 테스트를 구현한 것입니다.
from scipy.stats import jarque_bera
# Performing Jarque-Bera test
test_statistic, p_value = jarque_bera(response_var)
print("Jarque-Bera Test Statistic:", test_statistic)
print("P-value:", p_value)
# Interpreting results
alpha = 0.05
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")출력:

| 범주 | 모수적 통계 기법 | 비모수적 통계분석기법 |
| 상관 관계 | 피어슨 곱 모멘트 상관계수(r) | Spearman 순위 계수 상관 관계(Rho), Kendall의 Tau |
| 두 그룹, 독립적인 측정 | 독립 t-검정 | Mann-Whitney U 테스트 |
| 2개 이상의 그룹, 독립적인 조치 | 일원 분산 분석 | Kruskal-Wallis 일원 분산 분석 |
| 두 그룹, 반복 측정 | 쌍체 t-검정 | Wilcoxon 일치 쌍 부호 순위 테스트 |
| 2개 이상의 그룹, 반복 측정 | 일원 반복 측정 ANOVA | Friedman의 양방향 분산 분석 |
결론
가설 검증 표본 데이터를 사용하여 모집단 매개변수에 대한 주장을 평가하는 데 필수적입니다. 모수적 테스트는 특정 가정에 의존하며 간격 또는 비율 데이터에 적합한 반면, 비모수적 테스트는 더 유연하고 엄격한 분포 가정 없이 명목 또는 순서 데이터에 적용 가능합니다. Shapiro-Wilk 및 Anderson-Darling과 같은 검정은 정규성을 평가하고 Chi-square 및 Jarque-Bera는 적합도를 평가합니다. 적절한 통계적 접근법을 선택하려면 모수적 테스트와 비모수적 테스트의 차이점을 이해하는 것이 중요합니다. 전반적으로, 가설 테스트는 데이터 기반 결정을 내리고 경험적 증거로부터 신뢰할 수 있는 결론을 도출하기 위한 체계적인 프레임워크를 제공합니다.
고급 통계 분석을 마스터할 준비가 되셨나요? 지금 BlackBelt 데이터 분석 과정에 등록하세요! 가설 테스트, 모수적 및 비모수적 테스트, Python 구현 등에 대한 전문 지식을 얻으십시오. 통계 기술을 향상하고 데이터 기반 의사결정에 탁월한 능력을 발휘하세요. 지금 가입하세요!
자주 묻는 질문
A. 모수적 테스트는 모집단 분포와 매개변수(예: 정규성, 분산의 동질성)에 대한 가정을 하는 반면, 비모수적 테스트는 이러한 가정에 의존하지 않습니다. 모수적 테스트는 가정이 충족될 때 더 강력한 성능을 발휘하는 반면, 비모수적 테스트는 더 강력하고 데이터가 왜곡되거나 정규 분포가 아닌 경우를 포함하여 더 넓은 범위의 상황에 적용할 수 있습니다.
A. 카이제곱 검정은 두 범주형 변수 사이에 유의미한 연관성이 있는지 확인하는 데 사용됩니다. 일반적으로 범주형 데이터를 분석하고 분할표에서 변수의 독립성에 대한 가설을 테스트합니다.
A. Mann-Whitney U 검정은 종속변수가 순서형이거나 정규 분포가 아닐 때 두 개의 독립 그룹을 비교합니다. 두 그룹의 중앙값 간에 유의한 차이가 있는지 여부를 평가합니다.
A. Shapiro-Wilk 검정은 표본이 정규 분포 모집단에서 추출되었는지 여부를 평가합니다. 데이터가 정규 분포를 따른다는 귀무가설을 테스트합니다. p-값이 선택한 유의 수준(예: 0.05)보다 작으면 귀무 가설을 기각하고 데이터가 정규 분포를 따르지 않는다는 결론을 내립니다.
- SEO 기반 콘텐츠 및 PR 배포. 오늘 증폭하십시오.
- PlatoData.Network 수직 생성 Ai. 자신에게 권한을 부여하십시오. 여기에서 액세스하십시오.
- PlatoAiStream. 웹3 인텔리전스. 지식 증폭. 여기에서 액세스하십시오.
- 플라톤ESG. 탄소, 클린테크, 에너지, 환경, 태양광, 폐기물 관리. 여기에서 액세스하십시오.
- PlatoHealth. 생명 공학 및 임상 시험 인텔리전스. 여기에서 액세스하십시오.
- 출처: https://www.analyticsvidhya.com/blog/2024/04/a-comprehensive-guide-on-non-parametric-tests/



