Image par l'éditeur
 

Comme Karl Pearson, un mathématicien britannique l'a dit un jour, Statistique est la grammaire des sciences et cela vaut en particulier pour les sciences informatiques et de l'information, les sciences physiques et les sciences biologiques. Lorsque vous commencez votre voyage en Sciences des données or Analyse de Donnée, avoir des connaissances statistiques vous aidera à mieux exploiter les informations sur les données.

"La statistique est la grammaire de la science." Carl Pearson

L'importance des statistiques dans la science des données et l'analyse des données ne peut être sous-estimée. Les statistiques fournissent des outils et des méthodes pour trouver une structure et donner des informations plus approfondies sur les données. Les statistiques et les mathématiques aiment les faits et détestent les suppositions. Connaître les principes fondamentaux de ces deux sujets importants vous permettra de penser de manière critique et d'être créatif lorsque vous utilisez les données pour résoudre des problèmes commerciaux et prendre des décisions basées sur les données. Dans cet article, je couvrirai les sujets statistiques suivants pour la science des données et l'analyse de données :

- Random variables - Probability distribution functions (PDFs) - Mean, Variance, Standard Deviation - Covariance and Correlation - Bayes Theorem - Linear Regression and Ordinary Least Squares (OLS) - Gauss-Markov Theorem - Parameter properties (Bias, Consistency, Efficiency) - Confidence intervals - Hypothesis testing - Statistical significance - Type I & Type II Errors - Statistical tests (Student's t-test, F-test) - p-value and its limitations - Inferential Statistics - Central Limit Theorem & Law of Large Numbers - Dimensionality reduction techniques (PCA, FA)

Si vous n'avez aucune connaissance statistique préalable et que vous souhaitez identifier et apprendre les concepts statistiques essentiels à partir de zéro, pour vous préparer à vos entretiens d'embauche, cet article est pour vous. Cet article sera également une bonne lecture pour quiconque souhaite rafraîchir ses connaissances statistiques.

Voici le LunarTech.ai, où nous comprenons le pouvoir des stratégies de recherche d'emploi dans le domaine dynamique de la science des données et de l'IA. Nous approfondissons les tactiques et les stratégies nécessaires pour naviguer dans le processus de recherche d'emploi concurrentiel. Qu'il s'agisse de définir vos objectifs de carrière, de personnaliser les documents de candidature ou de tirer parti des sites d'emploi et du réseautage, nos informations vous fournissent les conseils dont vous avez besoin pour décrocher l'emploi de vos rêves.

Vous vous préparez pour des entretiens en science des données ? N'ayez pas peur ! Nous mettons en lumière les subtilités du processus d'entretien, en vous dotant des connaissances et de la préparation nécessaires pour augmenter vos chances de succès. Des premières présélections téléphoniques aux évaluations techniques, en passant par les entretiens techniques et les entretiens comportementaux, nous ne négligeons aucun effort.

At LunarTech.ai, nous allons au-delà de la théorie. Nous sommes votre tremplin vers un succès inégalé dans le domaine de la technologie et de la science des données. Notre parcours d'apprentissage complet est conçu pour s'adapter parfaitement à votre style de vie, vous permettant de trouver l'équilibre parfait entre les engagements personnels et professionnels tout en acquérant des compétences de pointe. Grâce à notre dévouement à l'évolution de votre carrière, y compris l'aide au placement, la rédaction de CV d'experts et la préparation aux entretiens, vous deviendrez une centrale prête pour l'industrie.

Rejoignez notre communauté d'individus ambitieux dès aujourd'hui et embarquez ensemble dans ce passionnant voyage en science des données. Avec LunarTech.ai, l'avenir est prometteur et vous détenez les clés pour débloquer des opportunités illimitées.

Le concept de variables aléatoires constitue la pierre angulaire de nombreux concepts statistiques. Il peut être difficile de digérer sa définition mathématique formelle, mais en termes simples, un Variable aléatoire est un moyen de mapper les résultats de processus aléatoires, tels que lancer une pièce ou lancer un dé, sur des nombres. Par exemple, nous pouvons définir le processus aléatoire de lancer une pièce par la variable aléatoire X qui prend une valeur 1 si le résultat si têtes et 0 si le résultat est queues.

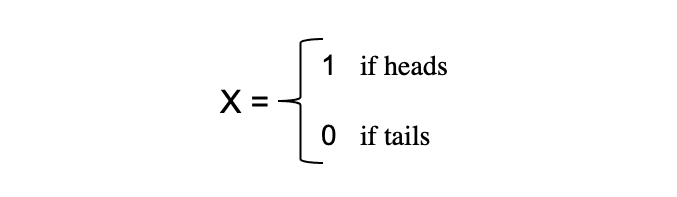
Dans cet exemple, nous avons un processus aléatoire de lancer une pièce où cette expérience peut produire deux résultats possibles: {0,1}. Cet ensemble de tous les résultats possibles est appelé le espace d'échantillon de l'expérience. Chaque fois que le processus aléatoire est répété, il est appelé un un événement. Dans cet exemple, lancer une pièce et obtenir pile comme résultat est un événement. La chance ou la probabilité que cet événement se produise avec un résultat particulier est appelée la probabilité de cet événement. Une probabilité d'un événement est la probabilité qu'une variable aléatoire prenne une valeur spécifique de x qui peut être décrite par P(x). Dans l'exemple du lancer d'une pièce, la probabilité d'obtenir pile ou face est la même, c'est-à-dire 0.5 ou 50 %. Nous avons donc le réglage suivant :

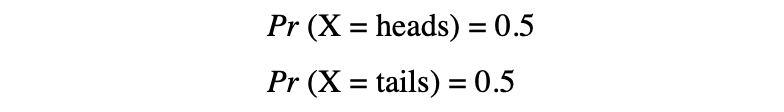
où la probabilité d'un événement, dans cet exemple, ne peut prendre que des valeurs comprises dans l'intervalle [0,1].

L'importance des statistiques dans la science des données et l'analyse des données ne peut être sous-estimée. Les statistiques fournissent des outils et des méthodes pour trouver une structure et donner des informations plus approfondies sur les données.

Pour comprendre les concepts de moyenne, de variance et de nombreux autres sujets statistiques, il est important d'apprendre les concepts de population ainsi que  échantillon. La population est l'ensemble de toutes les observations (individus, objets, événements ou procédures) et est généralement très vaste et diversifié, alors qu'un échantillon est un sous-ensemble d'observations de la population qui, idéalement, est une véritable représentation de la population.

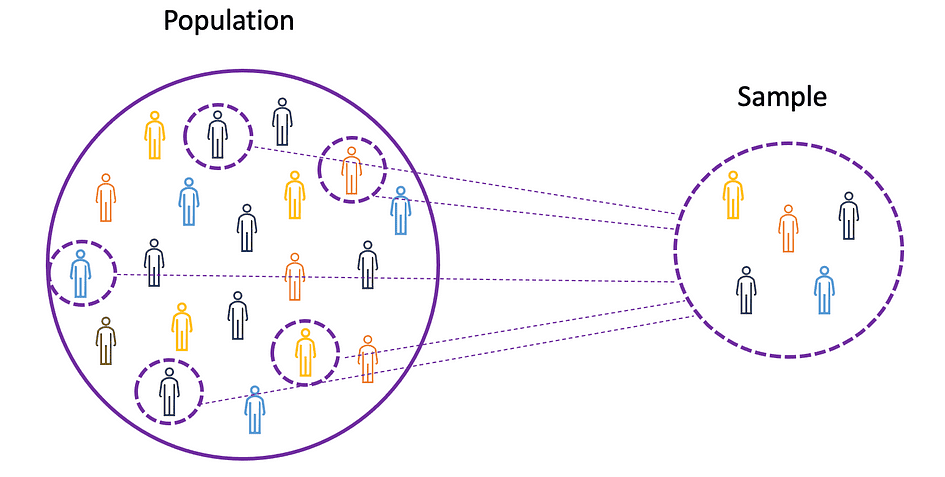
Source de l'image : l'auteur

Étant donné qu'expérimenter avec une population entière est soit impossible, soit tout simplement trop coûteux, les chercheurs ou les analystes utilisent des échantillons plutôt que la population entière dans leurs expériences ou essais. Pour s'assurer que les résultats expérimentaux sont fiables et valables pour l'ensemble de la population, l'échantillon doit être une représentation fidèle de la population. Autrement dit, l'échantillon doit être impartial. A cet effet, on peut utiliser des techniques d'échantillonnage statistique telles que Échantillonnage aléatoire, échantillonnage systématique, échantillonnage groupé, échantillonnage pondéré et échantillonnage stratifié.

Médian

La moyenne, également connue sous le nom de moyenne, est une valeur centrale d'un ensemble fini de nombres. Supposons qu'une variable aléatoire X dans les données ait les valeurs suivantes :

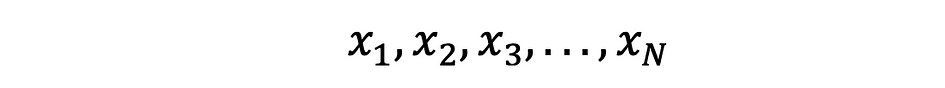
où N est le nombre d'observations ou de points de données dans l'ensemble d'échantillons ou simplement la fréquence des données. Puis le moyenne de l'échantillon Défini par ?, qui est très souvent utilisé pour approximer population signifie, peut s'exprimer comme suit :

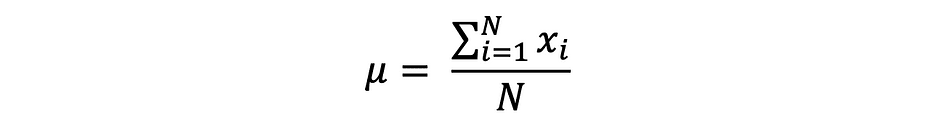
La moyenne est aussi appelée attente qui est souvent défini par E() ou variable aléatoire avec une barre en haut. Par exemple, l'espérance des variables aléatoires X et Y, c'est-à-dire E(X) et E(Y), respectivement, peut être exprimée comme suit :

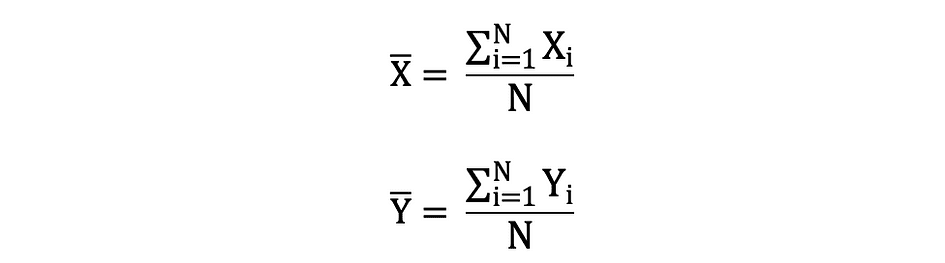
import numpy as np
import math
x = np.array([1,3,5,6])
mean_x = np.mean(x)
# in case the data contains Nan values
x_nan = np.array([1,3,5,6, math.nan])
mean_x_nan = np.nanmean(x_nan)

Variance

La variance mesure l'écart entre les points de données et la valeur moyenne, et est égal à la somme des carrés des différences entre les valeurs des données et la moyenne (la moyenne). En outre, le variance de la population, peut s'exprimer comme suit :

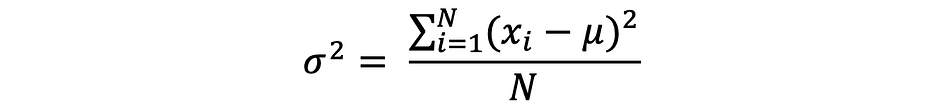
x = np.array([1,3,5,6])
variance_x = np.var(x) # here you need to specify the degrees of freedom (df) max number of logically independent data points that have freedom to vary
x_nan = np.array([1,3,5,6, math.nan])
mean_x_nan = np.nanvar(x_nan, ddof = 1)

Pour dériver les attentes et les variances de différentes fonctions de distribution de probabilité populaires, consultez ce dépôt Github.

L'écart-type

L'écart type est simplement la racine carrée de la variance et mesure la mesure dans laquelle les données varient par rapport à leur moyenne. L'écart type défini par sigma peut s'exprimer comme suit :

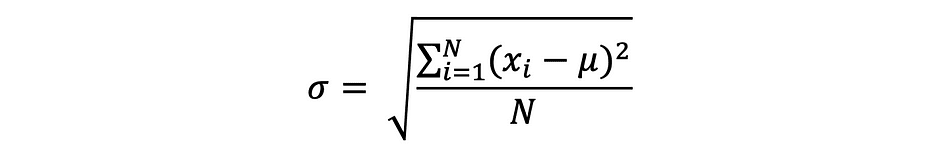
L'écart type est souvent préféré à la variance car il a la même unité que les points de données, ce qui signifie que vous pouvez l'interpréter plus facilement.

x = np.array([1,3,5,6])
variance_x = np.std(x) x_nan = np.array([1,3,5,6, math.nan])
mean_x_nan = np.nanstd(x_nan, ddof = 1)

Covariance

La covariance est une mesure de la variabilité conjointe de deux variables aléatoires et décrit la relation entre ces deux variables. Il est défini comme la valeur attendue du produit des écarts des deux variables aléatoires par rapport à leurs moyennes. La covariance entre deux variables aléatoires X et Z peut être décrite par l'expression suivante, où E(X) et E(Z) représentent les moyennes de X et Z, respectivement.

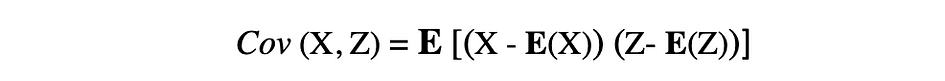
La covariance peut prendre des valeurs négatives ou positives ainsi que la valeur 0. Une valeur positive de covariance indique que deux variables aléatoires ont tendance à varier dans le même sens, alors qu'une valeur négative suggère que ces variables varient dans des directions opposées. Enfin, la valeur 0 signifie qu'ils ne varient pas ensemble.

x = np.array([1,3,5,6])
y = np.array([-2,-4,-5,-6])
#this will return the covariance matrix of x,y containing x_variance, y_variance on diagonal elements and covariance of x,y
cov_xy = np.cov(x,y)

Corrélation

La corrélation est également une mesure de la relation et elle mesure à la fois la force et la direction de la relation linéaire entre deux variables. Si une corrélation est détectée, cela signifie qu'il existe une relation ou un modèle entre les valeurs de deux variables cibles. La corrélation entre deux variables aléatoires X et Z est égale à la covariance entre ces deux variables divisée par le produit des écarts-types de ces variables qui peut être décrit par l'expression suivante.

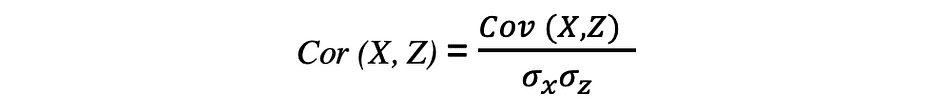
Les valeurs des coefficients de corrélation sont comprises entre -1 et 1. Gardez à l'esprit que la corrélation d'une variable avec elle-même est toujours de 1, c'est-à-dire Cor(X, X) = 1. Une autre chose à garder à l'esprit lors de l'interprétation de la corrélation est de ne pas la confondre avec lien de causalité, étant donné qu'une corrélation n'est pas une causalité. Même s'il existe une corrélation entre deux variables, vous ne pouvez pas conclure qu'une variable provoque un changement dans l'autre. Cette relation pourrait être fortuite, ou un troisième facteur pourrait faire changer les deux variables.

x = np.array([1,3,5,6])
y = np.array([-2,-4,-5,-6])
corr = np.corrcoef(x,y)

Une fonction qui décrit toutes les valeurs possibles, l'espace d'échantillonnage et les probabilités correspondantes qu'une variable aléatoire peut prendre dans une plage donnée, délimitée entre les valeurs minimales et maximales possibles, est appelée une fonction de distribution de probabilité (pdf) ou densité de probabilité. Chaque pdf doit satisfaire les deux critères suivants :

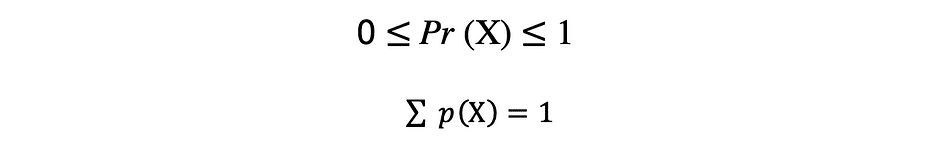
où le premier critère stipule que toutes les probabilités doivent être des nombres dans la plage de [0,1] et le deuxième critère stipule que la somme de toutes les probabilités possibles doit être égale à 1.

Les fonctions de probabilité sont généralement classées en deux catégories : discret ainsi que  continu. Discret distribution fonction décrit le processus aléatoire avec dénombrable espace échantillon, comme dans le cas d'un exemple de lancer une pièce qui n'a que deux résultats possibles. Continu fonction de distribution décrit le processus aléatoire avec continu espace d'échantillon. Des exemples de fonctions de distribution discrètes sont Bernoulli, Binôme, Poisson, Uniforme discret. Des exemples de fonctions de distribution continues sont Normal, Uniforme continu, cauché.

Distribution binomiale

La distribution binomiale est la distribution de probabilité discrète du nombre de succès dans une séquence de n expériences indépendantes, chacune avec le résultat booléen : succès (avec probabilité p) ou échec (avec probabilité q = 1 ? p). Supposons qu'une variable aléatoire X suit une distribution binomiale, alors la probabilité d'observer k les succès dans n essais indépendants peuvent être exprimés par la fonction de densité de probabilité suivante :

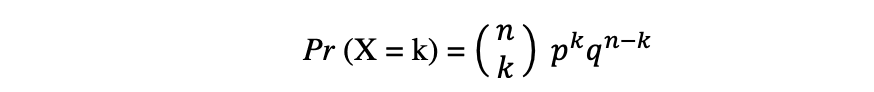
La distribution binomiale est utile lors de l'analyse des résultats d'expériences indépendantes répétées, en particulier si l'on s'intéresse à la probabilité d'atteindre un seuil particulier compte tenu d'un taux d'erreur spécifique.

Moyenne et variance de la distribution binomiale

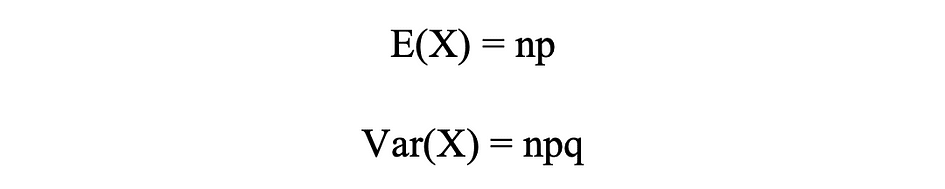
La figure ci-dessous visualise un exemple de distribution binomiale où le nombre d'essais indépendants est égal à 8 et la probabilité de succès dans chaque essai est égale à 16 %.

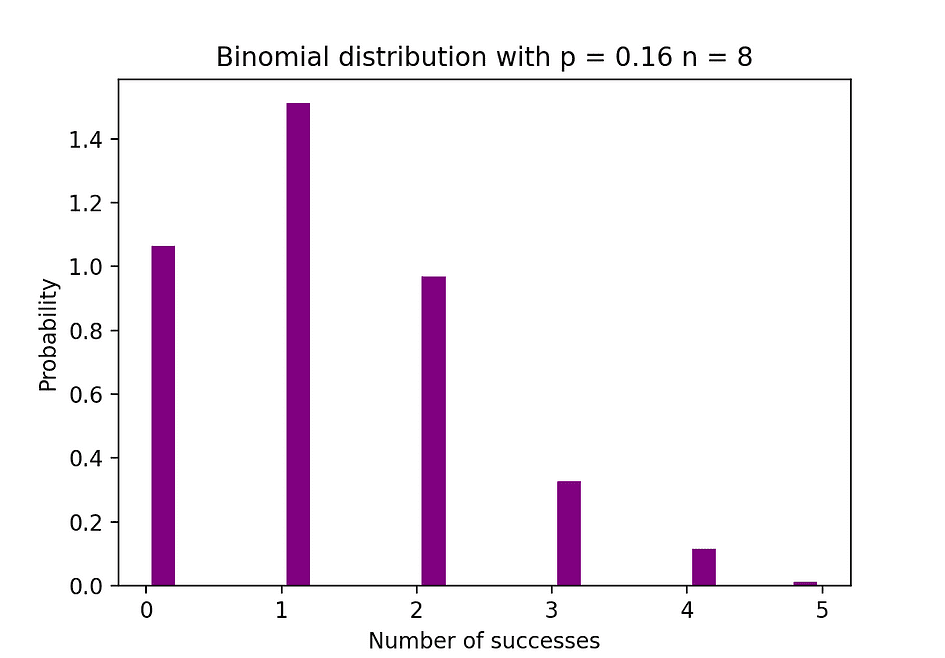
Source de l'image : l'auteur

# Random Generation of 1000 independent Binomial samples
import numpy as np
n = 8
p = 0.16
N = 1000
X = np.random.binomial(n,p,N)
# Histogram of Binomial distribution
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 20, density = True, rwidth = 0.7, color = 'purple')
plt.title("Binomial distribution with p = 0.16 n = 8")
plt.xlabel("Number of successes")
plt.ylabel("Probability")
plt.show()

Distribution de Poisson

La distribution de Poisson est la distribution de probabilité discrète du nombre d'événements se produisant au cours d'une période donnée, compte tenu du nombre moyen de fois où l'événement se produit au cours de cette période. Supposons qu'une variable aléatoire X suit une distribution de Poisson, alors la probabilité d'observer k événements sur une période de temps peuvent être exprimés par la fonction de probabilité suivante :

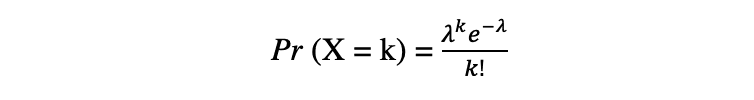
De e is le nombre d'Euler ainsi que  ? lambda, le paramètre de taux d'arrivée is la valeur attendue de X. La fonction de distribution de Poisson est très populaire pour son utilisation dans la modélisation d'événements dénombrables se produisant dans un intervalle de temps donné.

Distribution de Poisson Moyenne et variance

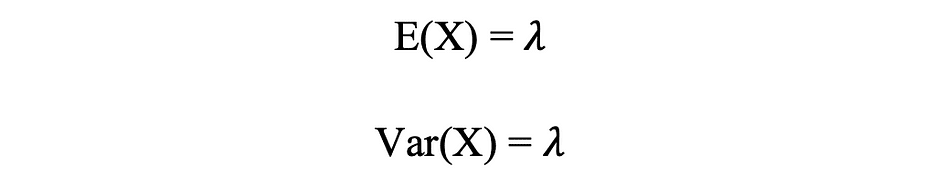
Par exemple, la distribution de Poisson peut être utilisée pour modéliser le nombre de clients arrivant dans le magasin entre 7h et 10h, ou le nombre de patients arrivant aux urgences entre 11h et 12h. La figure ci-dessous visualise un exemple de distribution de Poisson où l'on compte le nombre de visiteurs Web arrivant sur le site Web où le taux d'arrivée, lambda, est supposé être égal à 7 minutes.

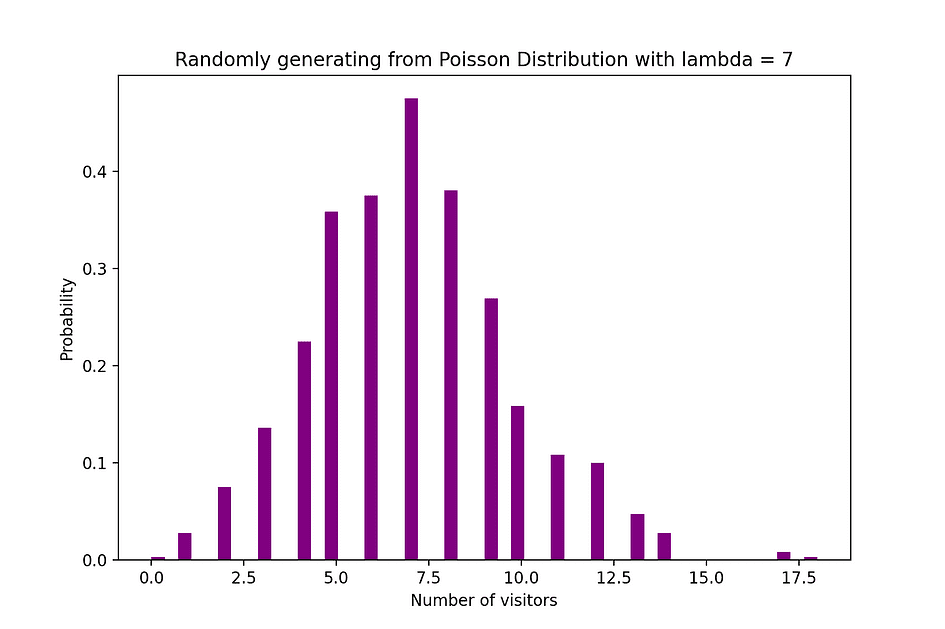
Source de l'image : l'auteur

# Random Generation of 1000 independent Poisson samples
import numpy as np
lambda_ = 7
N = 1000
X = np.random.poisson(lambda_,N) # Histogram of Poisson distribution
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 50, density = True, color = 'purple')
plt.title("Randomly generating from Poisson Distribution with lambda = 7")
plt.xlabel("Number of visitors")
plt.ylabel("Probability")
plt.show()

Distribution normale

La distribution de probabilité normale est la distribution de probabilité continue pour une variable aléatoire à valeur réelle. Distribution normale, aussi appelée Distribution gaussienne est sans doute l'une des fonctions de distribution les plus populaires couramment utilisées dans les sciences sociales et naturelles à des fins de modélisation, par exemple, elle est utilisée pour modéliser la taille des personnes ou les résultats des tests. Supposons qu'une variable aléatoire X suit une distribution normale, alors sa fonction de densité de probabilité peut être exprimée comme suit.

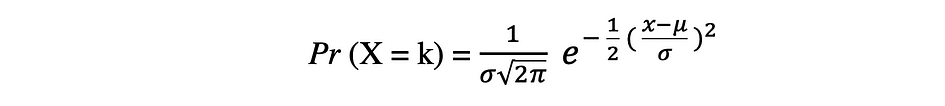
où le paramètre ? (mu) est la moyenne de la distribution également appelée paramètre de localisation, paramètre ? (sigme) est l'écart-type de la distribution, également appelé paramètre d'échelle. Le nombre ? (pi) est une constante mathématique approximativement égale à 3.14.

Moyenne et variance de la distribution normale

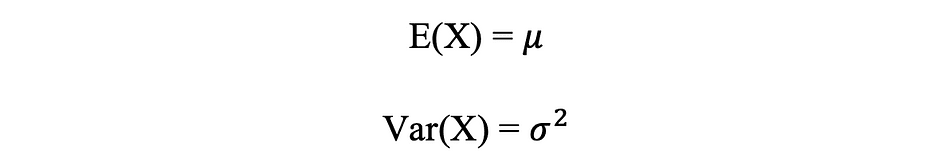
La figure ci-dessous visualise un exemple de distribution normale avec une moyenne de 0 (? = 0) et un écart type de 1 (? = 1), qui est appelé Normale Normale distribution qui est symétrique.

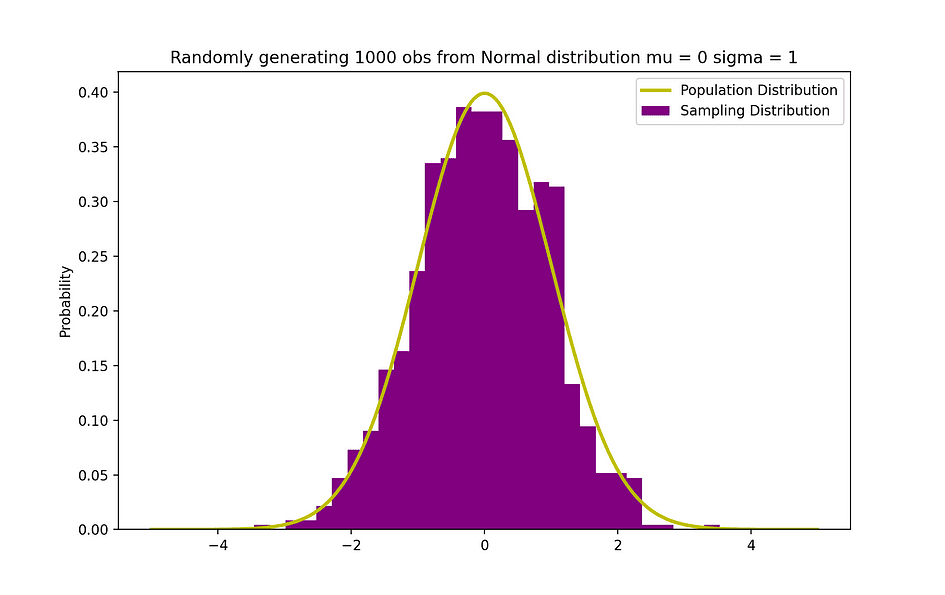
Source de l'image : l'auteur

# Random Generation of 1000 independent Normal samples
import numpy as np
mu = 0
sigma = 1
N = 1000
X = np.random.normal(mu,sigma,N) # Population distribution
from scipy.stats import norm
x_values = np.arange(-5,5,0.01)
y_values = norm.pdf(x_values)
#Sample histogram with Population distribution
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 30, density = True,color = 'purple',label = 'Sampling Distribution')
plt.plot(x_values,y_values, color = 'y',linewidth = 2.5,label = 'Population Distribution')
plt.title("Randomly generating 1000 obs from Normal distribution mu = 0 sigma = 1")
plt.ylabel("Probability")
plt.legend()
plt.show()

Le théorème de Bayes ou souvent appelé Loi de Bayes est sans doute la règle de probabilité et de statistique la plus puissante, du nom du célèbre statisticien et philosophe anglais Thomas Bayes.

Source de l'image: Wikipédia

Le théorème de Bayes est une puissante loi de probabilité qui amène le concept de subjectivité dans le monde des statistiques et des mathématiques où tout tourne autour des faits. Il décrit la probabilité d'un événement, sur la base des informations préalables de conditions qui pourrait être lié à cet événement. Par exemple, si le risque de contracter le coronavirus ou le Covid-19 est connu pour augmenter avec l'âge, alors le théorème de Bayes permet de déterminer plus précisément le risque pour un individu d'un âge connu en le conditionnant à l'âge plutôt qu'en supposant simplement que cet individu est commun à l'ensemble de la population.

La notion de probabilite conditionnelle, qui joue un rôle central dans la théorie de Bayes, est une mesure de la probabilité qu'un événement se produise, étant donné qu'un autre événement s'est déjà produit. Le théorème de Bayes peut être décrit par l'expression suivante où X et Y représentent respectivement les événements X et Y :

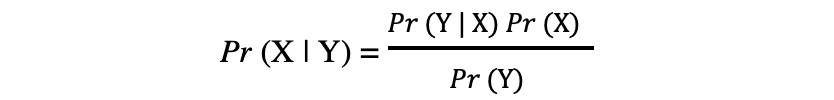
• Pr (X|Y) : la probabilité que l'événement X se produise étant donné que l'événement ou la condition Y s'est produit ou est vrai
• Pr (Y|X) : la probabilité que l'événement Y se produise étant donné que l'événement ou la condition X s'est produit ou est vrai
• Pr (X) & Pr (Y) : les probabilités d'observer les événements X et Y, respectivement

Dans le cas de l'exemple précédent, la probabilité de contracter le coronavirus (événement X) à condition d'être à un certain âge est Pr (X|Y), qui est égal à la probabilité d'être à un certain âge étant donné qu'on a attrapé un Coronavirus, Pr (Y|X), multiplié par la probabilité de contracter un Coronavirus, Pr (X), divisé par la probabilité d'être à un certain âge., Pr (Y).

Plus tôt, le concept de causalité entre les variables a été introduit, ce qui se produit lorsqu'une variable a un impact direct sur une autre variable. Lorsque la relation entre deux variables est linéaire, la régression linéaire est une méthode statistique qui peut aider à modéliser l'impact d'un changement d'unité dans une variable, le variable indépendante sur les valeurs d'une autre variable, la variable dépendante.

Les variables dépendantes sont souvent appelées variables de réponse or expliqué les variables, alors que les variables indépendantes sont souvent appelées régresseurs or variables explicatives. Lorsque le modèle de régression linéaire est basé sur une seule variable indépendante, le modèle est appelé Régression linéaire simple et lorsque le modèle est basé sur plusieurs variables indépendantes, il est appelé La régression linéaire multiple. La régression linéaire simple peut être décrite par l'expression suivante :

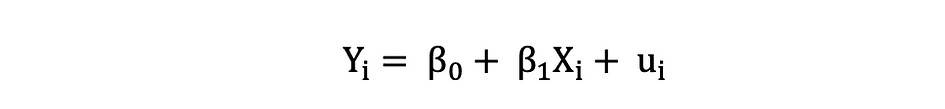
De Y est la variable dépendante, X est la variable indépendante qui fait partie des données, ?0 est l'ordonnée à l'origine qui est inconnue et constante, ?1 est le coefficient de pente ou un paramètre correspondant à la variable X qui est également inconnue et constante. Enfin, u est le terme d'erreur que le modèle fait lors de l'estimation des valeurs Y. L'idée principale derrière la régression linéaire est de trouver la ligne droite la mieux ajustée, la droite de régression, à travers un ensemble de données appariées ( X, Y ). Un exemple d'application de régression linéaire est la modélisation de l'impact de Longueur de la nageoire sur les pingouins Masse corporelle, qui est visualisé ci-dessous.

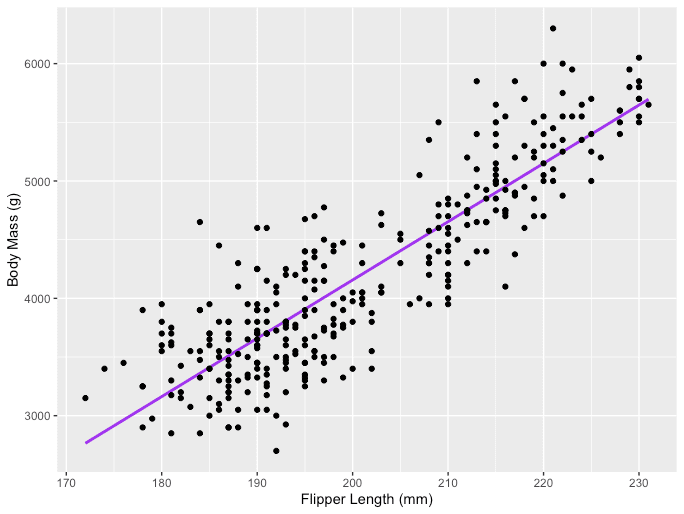
Source de l'image : l'auteur

# R code for the graph
install.packages("ggplot2")
install.packages("palmerpenguins")
library(palmerpenguins)
library(ggplot2)
View(data(penguins))
ggplot(data = penguins, aes(x = flipper_length_mm,y = body_mass_g))+ geom_smooth(method = "lm", se = FALSE, color = 'purple')+ geom_point()+ labs(x="Flipper Length (mm)",y="Body Mass (g)")

La régression linéaire multiple à trois variables indépendantes peut être décrite par l'expression suivante :

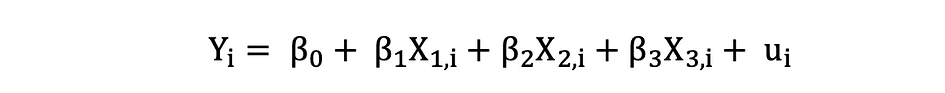
Moindres carrés ordinaires

Les moindres carrés ordinaires (MCO) sont une méthode d'estimation des paramètres inconnus tels que ?0 et ?1 dans un modèle de régression linéaire. Le modèle est basé sur le principe de moindres carrés qui minimise la somme des carrés des différences entre la variable dépendante observée et ses valeurs prédites par la fonction linéaire de la variable indépendante, souvent appelée valeurs ajustées. Cette différence entre les valeurs réelles et prédites de la variable dépendante Y est appelée résiduel et ce que fait OLS, c'est minimiser la somme des résidus au carré. Ce problème d'optimisation se traduit par les estimations MCO suivantes pour les paramètres inconnus ?0 et ?1 qui sont également connus sous le nom de estimations des coefficients.

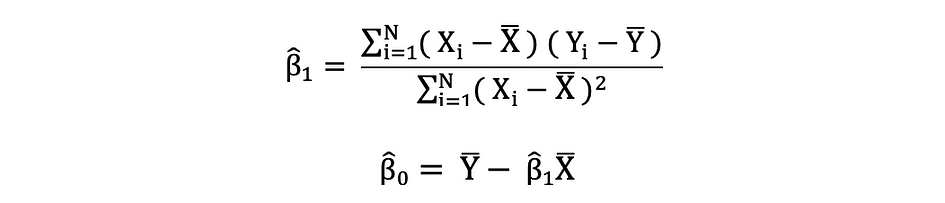
Une fois ces paramètres du modèle de régression linéaire simple estimés, la valeurs ajustées de la variable de réponse peut être calculée comme suit :

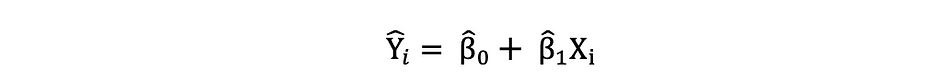
Erreur standard

La résidus ou les termes d'erreur estimés peuvent être déterminés comme suit :

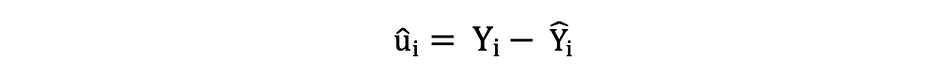
Il est important de garder à l'esprit la différence entre les termes d'erreur et les résidus. Les termes d'erreur ne sont jamais observés, tandis que les résidus sont calculés à partir des données. L'OLS estime les termes d'erreur pour chaque observation, mais pas le terme d'erreur réel. Ainsi, la véritable variance d'erreur est encore inconnue. De plus, ces estimations sont sujettes à l'incertitude d'échantillonnage. Cela signifie que nous ne pourrons jamais déterminer l'estimation exacte, la vraie valeur, de ces paramètres à partir de données d'échantillon dans une application empirique. Cependant, nous pouvons l'estimer en calculant échantillon variance résiduelle en utilisant les résidus comme suit.

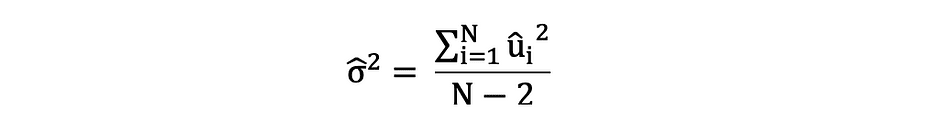
Cette estimation de la variance des résidus de l'échantillon aide à estimer la variance des paramètres estimés qui est souvent exprimée comme suit :

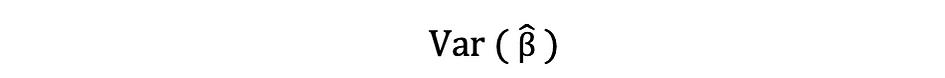
La racine carrée de ce terme de variance est appelée l'erreur standard de l'estimation qui est un élément clé dans l'évaluation de l'exactitude des estimations des paramètres. Il est utilisé pour calculer les statistiques de test et les intervalles de confiance. L'erreur type peut être exprimée comme suit :

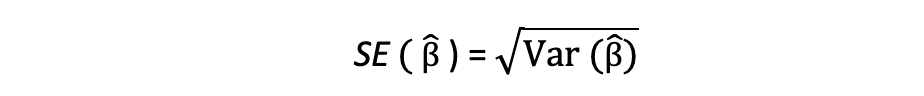
Il est important de garder à l'esprit la différence entre les termes d'erreur et les résidus. Les termes d'erreur ne sont jamais observés, tandis que les résidus sont calculés à partir des données.

Hypothèses MCO

La méthode d'estimation OLS fait l'hypothèse suivante qui doit être satisfaite pour obtenir des résultats de prédiction fiables :

A1 : Linéarité hypothèse stipule que le modèle est linéaire en paramètres.

A2: aléatoire Échantillon hypothèse stipule que toutes les observations de l'échantillon sont sélectionnées au hasard.

A3 : Exogénéité hypothèse stipule que les variables indépendantes ne sont pas corrélées avec les termes d'erreur.

A4 : Homoscédasticité hypothèse stipule que la variance de tous les termes d'erreur est constante.

A5 : Pas de multi-colinéarité parfaite L'hypothèse stipule qu'aucune des variables indépendantes n'est constante et qu'il n'y a pas de relations linéaires exactes entre les variables indépendantes.

def runOLS(Y,X): # OLS esyimation Y = Xb + e --> beta_hat = (X'X)^-1(X'Y) beta_hat = np.dot(np.linalg.inv(np.dot(np.transpose(X), X)), np.dot(np.transpose(X), Y)) # OLS prediction Y_hat = np.dot(X,beta_hat) residuals = Y-Y_hat RSS = np.sum(np.square(residuals)) sigma_squared_hat = RSS/(N-2) TSS = np.sum(np.square(Y-np.repeat(Y.mean(),len(Y)))) MSE = sigma_squared_hat RMSE = np.sqrt(MSE) R_squared = (TSS-RSS)/TSS # Standard error of estimates:square root of estimate's variance var_beta_hat = np.linalg.inv(np.dot(np.transpose(X),X))*sigma_squared_hat SE = [] t_stats = [] p_values = [] CI_s = [] for i in range(len(beta)): #standard errors SE_i = np.sqrt(var_beta_hat[i,i]) SE.append(np.round(SE_i,3)) #t-statistics t_stat = np.round(beta_hat[i,0]/SE_i,3) t_stats.append(t_stat) #p-value of t-stat p[|t_stat| >= t-treshhold two sided] p_value = t.sf(np.abs(t_stat),N-2) * 2 p_values.append(np.round(p_value,3)) #Confidence intervals = beta_hat -+ margin_of_error t_critical = t.ppf(q =1-0.05/2, df = N-2) margin_of_error = t_critical*SE_i CI = [np.round(beta_hat[i,0]-margin_of_error,3), np.round(beta_hat[i,0]+margin_of_error,3)] CI_s.append(CI) return(beta_hat, SE, t_stats, p_values,CI_s, MSE, RMSE, R_squared)

Sous l'hypothèse que les critères MCO A1 — A5 sont satisfaits, les estimateurs MCO des coefficients β0 et β1 sont BLEU ainsi que  Pertinence :.

Théorème de Gauss-Markov

Ce théorème met en évidence les propriétés des estimations MCO où le terme BLEU peuplements pour Meilleur estimateur linéaire sans biais.

Préjugé

La biais d'un estimateur est la différence entre sa valeur attendue et la vraie valeur du paramètre estimé et peut être exprimée comme suit :

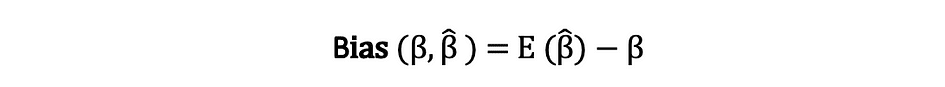
Lorsque nous disons que l'estimateur est impartial ce que nous voulons dire, c'est que le biais est égal à zéro, ce qui implique que la valeur attendue de l'estimateur est égale à la vraie valeur du paramètre, c'est-à-dire :

L'impartialité ne garantit pas que l'estimation obtenue avec un échantillon particulier est égale ou proche de ?. Cela signifie que, si l'on à plusieurs reprises tire des échantillons aléatoires de la population, puis calcule l'estimation à chaque fois, alors la moyenne de ces estimations serait égale ou très proche de β.

Efficacité

Le terme Les meilleurs dans le théorème de Gauss-Markov se rapporte à la variance de l'estimateur et est appelé efficace. Un paramètre peut avoir plusieurs estimateurs mais celui dont la variance est la plus faible est appelé efficace.

Cohérence

Le terme cohérence va de pair avec les termes taille de l'échantillon ainsi que  convergence. Si l'estimateur converge vers le vrai paramètre lorsque la taille de l'échantillon devient très grande, alors cet estimateur est dit cohérent, c'est-à-dire :

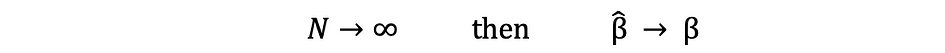
Sous l'hypothèse que les critères MCO A1 — A5 sont satisfaits, les estimateurs MCO des coefficients β0 et β1 sont BLEU ainsi que  Pertinence :.
Théorème de Gauss-Markov

Toutes ces propriétés sont valables pour les estimations OLS telles que résumées dans le théorème de Gauss-Markov. En d'autres termes, les estimations MCO ont la plus petite variance, elles sont impartiales, linéaires dans leurs paramètres et cohérentes. Ces propriétés peuvent être prouvées mathématiquement en utilisant les hypothèses OLS faites précédemment.

L'intervalle de confiance est la plage qui contient le vrai paramètre de population avec une certaine probabilité prédéfinie, appelée un niveau de confiance de l'expérience, et il est obtenu en utilisant les résultats de l'échantillon et le marge d'erreur.

Marge d'erreur

La marge d'erreur est la différence entre les résultats de l'échantillon et basée sur ce que le résultat aurait été si l'on avait utilisé l'ensemble de la population.

Un niveau de confiance

Le niveau de confiance décrit le niveau de certitude des résultats expérimentaux. Par exemple, un niveau de confiance de 95 % signifie que si l'on devait effectuer la même expérience à plusieurs reprises 100 fois, alors 95 de ces 100 essais conduiraient à des résultats similaires. Notez que le niveau de confiance est défini avant le début de l'expérience car il affectera la taille de la marge d'erreur à la fin de l'expérience.

Intervalle de confiance pour les estimations MCO

Comme il a été mentionné précédemment, les estimations MCO de la régression linéaire simple, les estimations pour l'ordonnée à l'origine ?0 et le coefficient de pente ?1, sont sujettes à l'incertitude d'échantillonnage. Cependant, nous pouvons construire des CI pour ces paramètres qui contiendra la vraie valeur de ces paramètres dans 95% de tous les échantillons. C'est-à-dire un intervalle de confiance à 95 % pour ? peut être interprété comme suit :

• L'intervalle de confiance est l'ensemble des valeurs pour lesquelles un test d'hypothèse ne peut pas être rejeté au seuil de 5 %.
• L'intervalle de confiance a 95 % de chance de contenir la vraie valeur de ?.

L'intervalle de confiance à 95 % des estimations MCO peut être construit comme suit :

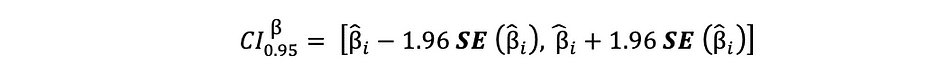
qui est basé sur l'estimation du paramètre, l'erreur type de cette estimation et la valeur 1.96 représentant la marge d'erreur correspondant à la règle de rejet de 5 %. Cette valeur est déterminée à l'aide de la Tableau de distribution normale, dont il sera question plus loin dans cet article. En attendant, la figure suivante illustre l'idée d'un IC à 95 % :

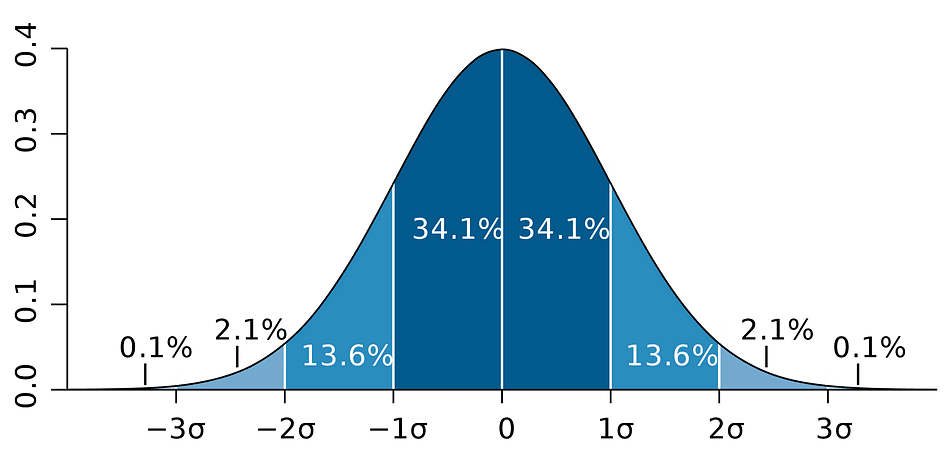
Source de l'image: Wikipédia

Notez que l'intervalle de confiance dépend également de la taille de l'échantillon, étant donné qu'il est calculé à l'aide de l'erreur type qui est basée sur la taille de l'échantillon.

Le niveau de confiance est défini avant le début de l'expérience car il affectera la taille de la marge d'erreur à la fin de l'expérience.

Tester une hypothèse dans Statistics est un moyen de tester les résultats d'une expérience ou d'une enquête afin de déterminer la pertinence des résultats. Fondamentalement, on teste si les résultats obtenus sont valides en déterminant les chances que les résultats se soient produits par hasard. Si c'est la lettre, alors les résultats ne sont pas fiables et l'expérience non plus. Le test d'hypothèse fait partie de la Inférence statistique.

Hypothèse nulle et alternative

Tout d'abord, vous devez déterminer la thèse que vous souhaitez tester, puis vous devez formuler la Hypothèse nulle et par Hypothèse alternative. Le test peut avoir deux résultats possibles et sur la base des résultats statistiques, vous pouvez soit rejeter l'hypothèse énoncée, soit l'accepter. En règle générale, les statisticiens ont tendance à placer la version ou la formulation de l'hypothèse sous l'hypothèse nulle selon laquelle qu'il faut rejeter, considérant que la version acceptable et souhaitée est indiquée sous l'hypothèse alternative.

Signification statistique

Regardons l'exemple mentionné précédemment où le modèle de régression linéaire a été utilisé pour déterminer si un pingouin Longueur de la nageoire, la variable indépendante, a un impact sur Masse corporelle, la variable dépendante. On peut formuler ce modèle avec l'expression statistique suivante :

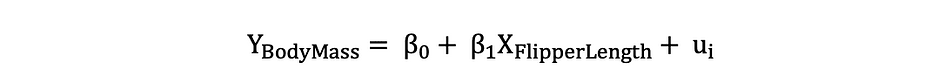
Ensuite, une fois que les estimations MCO des coefficients sont estimées, nous pouvons formuler l'hypothèse nulle et alternative suivante pour tester si la longueur du batteur a une statistiquement significatif impact sur la Masse Corporelle :

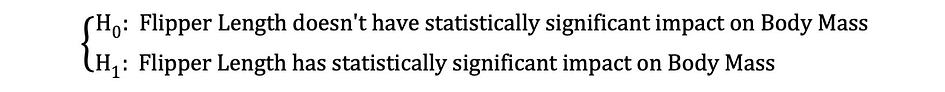
où H0 et H1 représentent respectivement l'hypothèse nulle et l'hypothèse alternative. Rejeter l'hypothèse nulle signifierait qu'une augmentation d'une unité de Longueur de la nageoire a un impact direct sur la Masse corporelle. Étant donné que l'estimation du paramètre de ?1 décrit cet impact de la variable indépendante, Longueur de la nageoire, sur la variable dépendante, Masse corporelle. Cette hypothèse peut être reformulée comme suit :

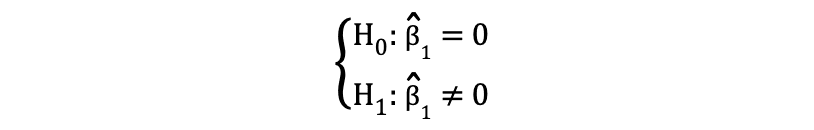
où H0 indique que l'estimation du paramètre de ?1 est égale à 0, c'est-à-dire Longueur de la nageoire effectuer sur Masse corporelle is statistiquement insignifiant Les H0 indique que l'estimation du paramètre de ?1 n'est pas égale à 0, ce qui suggère que Longueur de la nageoire effectuer sur Masse corporelle is statistiquement significatif.

Erreurs de type I et de type II

Lors de l'exécution d'un test d'hypothèse statistique, il faut tenir compte de deux types conceptuels d'erreurs : l'erreur de type I et l'erreur de type II. L'erreur de type I se produit lorsque l'hypothèse nulle est rejetée à tort, tandis que l'erreur de type II se produit lorsque l'hypothèse nulle n'est pas rejetée à tort. Une confusion matrice peut aider à visualiser clairement la gravité de ces deux types d'erreurs.

En règle générale, les statisticiens ont tendance à placer la version de l'hypothèse sous la Hypothèse nulle qui qu'il faut rejeter, alors que la version acceptable et souhaitée est indiquée sous le Hypothèse alternative.

Une fois que les hypothèses nulle et alternative sont énoncées et que les hypothèses de test sont définies, l'étape suivante consiste à déterminer quel test statistique est approprié et à calculer le statistique de test. Le fait de rejeter ou de ne pas rejeter le Null peut être déterminé en comparant la statistique de test avec le valeur critique. Cette comparaison montre si oui ou non la statistique de test observée est plus extrême que la valeur critique définie et elle peut avoir deux résultats possibles :

• La statistique de test est plus extrême que la valeur critique ? l'hypothèse nulle peut être rejetée
• La statistique de test n'est pas aussi extrême que la valeur critique ? l'hypothèse nulle ne peut pas être rejetée

La valeur critique est basée sur une valeur prédéfinie niveau de signification ? (généralement choisi égal à 5 ​​%) et le type de distribution de probabilité suivi par la statistique de test. La valeur critique divise l'aire sous cette courbe de distribution de probabilité en région(s) de rejet ainsi que  région de non-rejet. Il existe de nombreux tests statistiques permettant de tester diverses hypothèses. Des exemples de tests statistiques sont Test t de Student, Test F, Test du chi carré, Test d'endogénéité de Durbin-Hausman-Wu, Danstest d'hétéroscédasticité. Dans cet article, nous examinerons deux de ces tests statistiques.

L'erreur de type I se produit lorsque l'hypothèse nulle est rejetée à tort, tandis que l'erreur de type II se produit lorsque l'hypothèse nulle n'est pas rejetée à tort.

Test t de Student

L'un des tests statistiques les plus simples et les plus populaires est le test t de Student. qui peut être utilisé pour tester diverses hypothèses, en particulier lorsqu'il s'agit d'une hypothèse où le principal domaine d'intérêt est de trouver des preuves de l'effet statistiquement significatif d'un variable unique. La les statistiques de test du test t suivent Distribution t de Student et peut être déterminé comme suit :

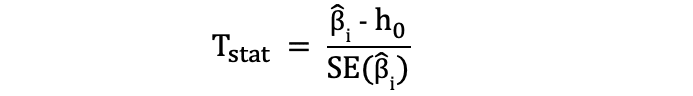
où h0 dans le nominateur est la valeur par rapport à laquelle l'estimation du paramètre est testée. Ainsi, les statistiques du test t sont égales à l'estimation du paramètre moins la valeur hypothétique divisée par l'erreur type de l'estimation du coefficient. Dans l'hypothèse énoncée précédemment, où nous voulions tester si la longueur de la nageoire avait un impact statistiquement significatif sur la masse corporelle ou non. Ce test peut être effectué à l'aide d'un test t et le h0 est dans ce cas égal au 0 puisque l'estimation du coefficient de pente est testée par rapport à la valeur 0.

Il existe deux versions du test t : un test t bilatéral et test t unilatéral. Que vous ayez besoin de la première ou de la dernière version du test dépend entièrement de l'hypothèse que vous souhaitez tester.

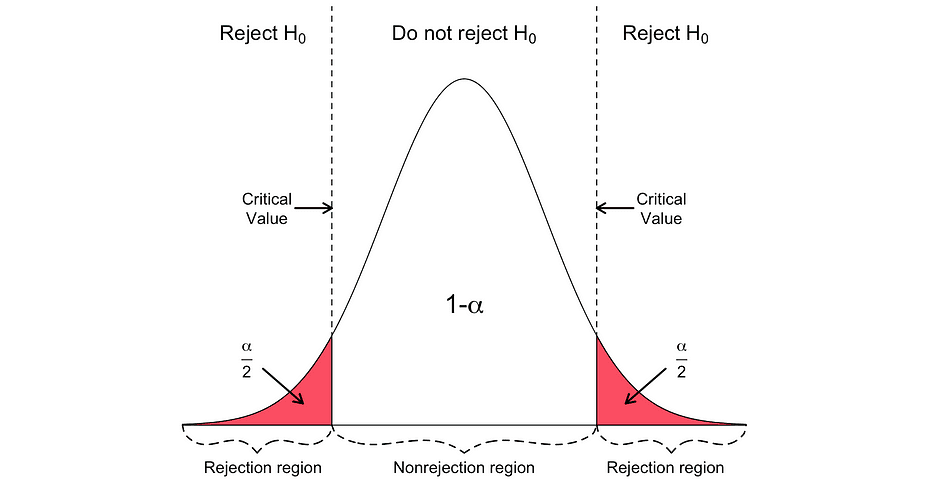
Le bilatéral or test t bilatéral peut être utilisé lorsque l'hypothèse teste égal versus inégal relation sous les hypothèses nulle et alternative similaire à l'exemple suivant :

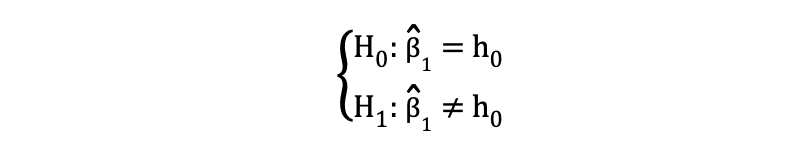
Le test t bilatéral a deux régions de rejet comme visualisé dans la figure ci-dessous :

Source de l'image: Hartmann, K., Krois, J., Waske, B. (2018) : Projet d'apprentissage en ligne SOGA : Statistiques et analyse de données géospatiales. Département des sciences de la Terre, Freie Universitaet Berlin

Dans cette version du test t, la valeur Null est rejetée si la statistique t calculée est trop petite ou trop grande.

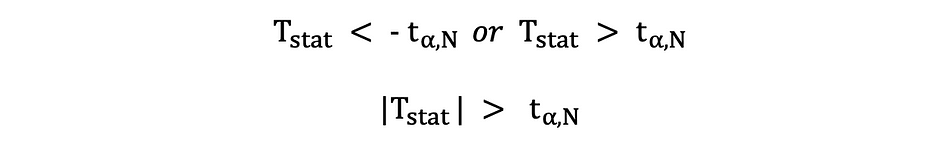
Ici, les statistiques de test sont comparées aux valeurs critiques basées sur la taille de l'échantillon et le niveau de signification choisi. Pour déterminer la valeur exacte du point de coupure, la table de distribution t bilatérale peut être utilisé.

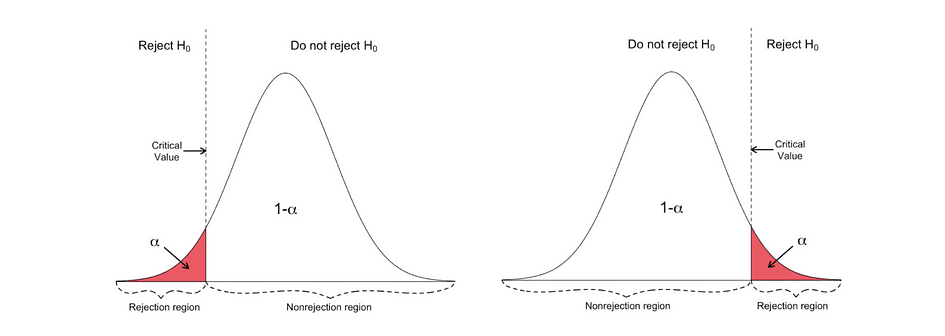
Le unilatéral ou test t unilatéral peut être utilisé lorsque l'hypothèse teste positif négatif versus négatif positif relation sous les hypothèses nulle et alternative qui est similaire aux exemples suivants :

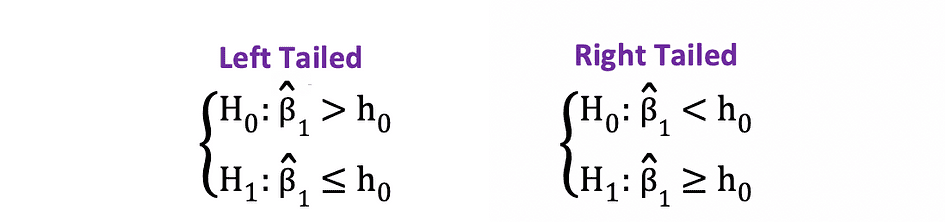
Le test t unilatéral a un unique région de rejet et selon du côté de l'hypothèse, la région de rejet est soit du côté gauche, soit du côté droit, comme illustré dans la figure ci-dessous :

Source de l'image: Hartmann, K., Krois, J., Waske, B. (2018) : Projet d'apprentissage en ligne SOGA : Statistiques et analyse de données géospatiales. Département des sciences de la Terre, Freie Universitaet Berlin

Dans cette version du test t, le Null est rejeté si la statistique t calculée est inférieure/supérieure à la valeur critique.

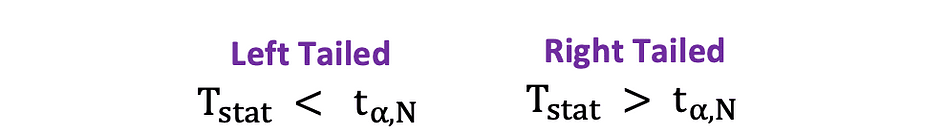
Test F

Le test F est un autre test statistique très populaire souvent utilisé pour tester des hypothèses. a signification statistique conjointe de plusieurs variables. C'est le cas lorsque vous souhaitez tester si plusieurs variables indépendantes ont un impact statistiquement significatif sur une variable dépendante. Voici un exemple d'hypothèse statistique qui peut être testée à l'aide du test F :

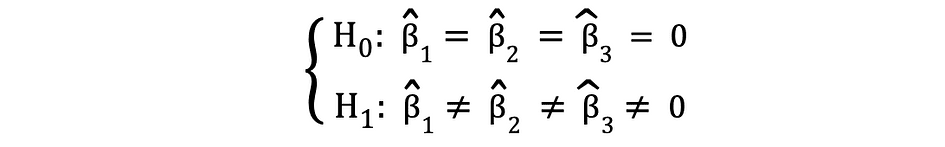
où le Null indique que les trois variables correspondant à ces coefficients sont conjointement statistiquement non significatives et l'Alternative indique que ces trois variables sont conjointement statistiquement significatives. Les statistiques de test du test F suivent Distribution F et peut être déterminé comme suit :

où le SSRrestreint est le somme des carrés des résidus des limité modèle qui est le même modèle en excluant des données les variables cibles déclarées comme non significatives sous le Null, le SSRunrestricted est la somme des résidus au carré des libre modèle qui est le modèle qui inclut toutes les variables, le q représente le nombre de variables qui sont testées conjointement pour l'insignifiance sous le Null, N est la taille de l'échantillon et le k est le nombre total de variables dans le modèle sans restriction. Les valeurs SSR sont fournies à côté des estimations des paramètres après l'exécution de la régression OLS et il en va de même pour les statistiques F. Voici un exemple de sortie de modèle MLR où les valeurs SSR et F-statistics sont marquées.

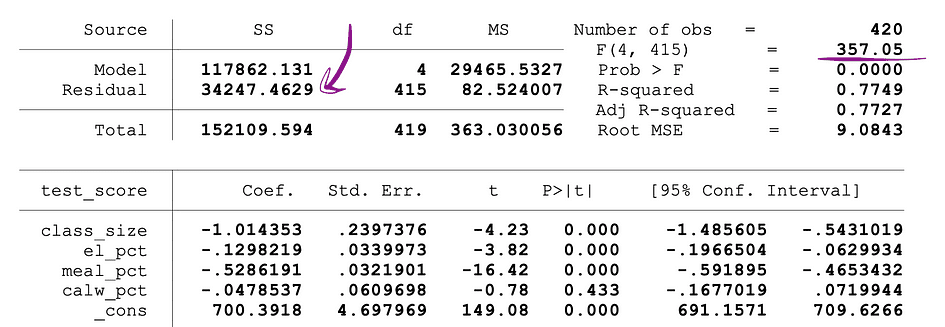
Source de l'image: Stock et Whatson

Le test F a une seule région de rejet comme visualisé ci-dessous :

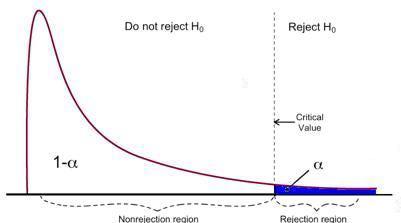
Source de l'image: Université du Michigan

Si la statistique F calculée est supérieure à la valeur critique, alors le Null peut être rejeté, ce qui suggère que les variables indépendantes sont conjointement statistiquement significatives. La règle de rejet peut être exprimée comme suit :

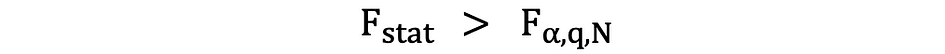
Un autre moyen rapide de déterminer s'il faut rejeter ou soutenir l'hypothèse nulle consiste à utiliser valeurs p. La valeur de p est la probabilité que la condition sous le Null se produise. En d'autres termes, la valeur de p est la probabilité, en supposant que l'hypothèse nulle est vraie, d'observer un résultat au moins aussi extrême que la statistique de test. Plus la valeur p est petite, plus la preuve contre l'hypothèse nulle est forte, ce qui suggère qu'elle peut être rejetée.

L'interprétation d'un p-la valeur dépend du niveau de signification choisi. Le plus souvent, des seuils de signification de 1 %, 5 % ou 10 % sont utilisés pour interpréter la valeur de p. Ainsi, au lieu d'utiliser le test t et le test F, les valeurs p de ces statistiques de test peuvent être utilisées pour tester les mêmes hypothèses.

La figure suivante montre un exemple de sortie d'une régression OLS avec deux variables indépendantes. Dans ce tableau, la valeur p du test t, testant la signification statistique de taille_classe l'estimation du paramètre de la variable et la valeur p du test F, testant la signification statistique conjointe de la taille_classe, ainsi que  el_pct estimations des paramètres des variables, sont soulignés.

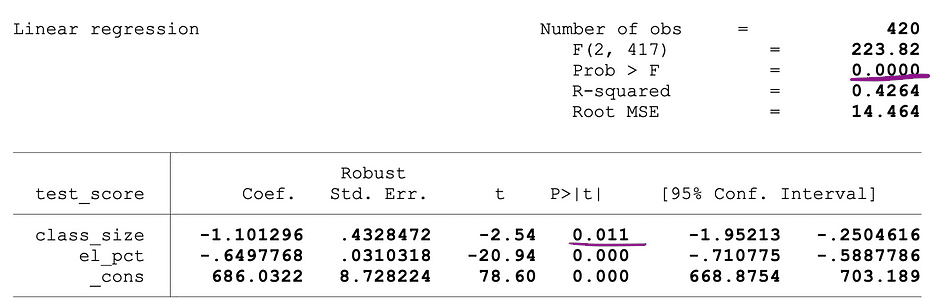
Source de l'image: Stock et Whatson

La valeur de p correspondant à la taille_classe est de 0.011 et lorsque l'on compare cette valeur aux niveaux de signification 1 % ou 0.01 , 5 % ou 0.05, 10 % ou 0.1, les conclusions suivantes peuvent être tirées :

• 0.011 > 0.01 ? La valeur nulle du test t ne peut pas être rejetée au niveau de signification de 1 %
• 0.011 < 0.05 ? La valeur nulle du test t peut être rejetée à un niveau de signification de 5 %
• 0.011 < 0.10 ?La valeur nulle du test t peut être rejetée à un seuil de signification de 10 %

Ainsi, cette valeur de p suggère que le coefficient de la taille_classe variable est statistiquement significative à des niveaux de signification de 5 % et 10 %. La valeur p correspondant au test F est 0.0000 et puisque 0 est plus petit que les trois valeurs seuils ; 0.01, 0.05, 0.10, on peut conclure que le Null du F-test peut être rejeté dans les trois cas. Ceci suggère que les coefficients de taille_classe ainsi que  el_pct les variables sont conjointement statistiquement significatives à des niveaux de signification de 1 %, 5 % et 10 %.

Limitation des valeurs p

Bien que l'utilisation des p-values ​​présente de nombreux avantages, elle présente également des limites. À savoir, la valeur p dépend à la fois de l'ampleur de l'association et de la taille de l'échantillon. Si l'ampleur de l'effet est faible et statistiquement insignifiante, la valeur de p peut toujours montrer un impact significatif parce que la grande taille de l'échantillon est grande. L'inverse peut également se produire, un effet peut être important, mais ne pas répondre aux critères p<0.01, 0.05 ou 0.10 si la taille de l'échantillon est petite.

Les statistiques inférentielles utilisent des données d'échantillon pour porter des jugements raisonnables sur la population d'où proviennent les données d'échantillon. Il est utilisé pour étudier les relations entre les variables au sein d'un échantillon et faire des prédictions sur la façon dont ces variables seront liées à une population plus large.

Les deux  Loi des grands nombres (LLN) ainsi que  Théorème central limite (CLM) ont un rôle important dans les statistiques inférentielles car elles montrent que les résultats expérimentaux sont valables quelle que soit la forme de la distribution de la population d'origine lorsque les données sont suffisamment grandes. Plus les données sont collectées, plus les inférences statistiques deviennent précises, par conséquent, plus les estimations de paramètres sont générées.

Loi des grands nombres (LLN)

Supposer X1, X2, . . . , Xn sont toutes des variables aléatoires indépendantes avec la même distribution sous-jacente, également appelées indépendantes à distribution identique ou iid, où tous les X ont la même moyenne ? et écart type ?. À mesure que la taille de l'échantillon augmente, la probabilité que la moyenne de tous les X soit égale à la moyenne ? est égal à 1. La loi des grands nombres peut être résumée comme suit :

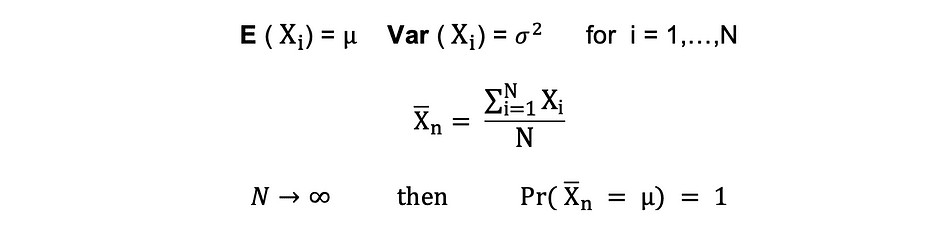
Théorème central limite (CLM)

Supposer X1, X2, . . . , Xn sont toutes des variables aléatoires indépendantes avec la même distribution sous-jacente, également appelées indépendantes à distribution identique ou iid, où tous les X ont la même moyenne ? et écart type ?. À mesure que la taille de l'échantillon augmente, la distribution de probabilité de X converge dans la distribution en distribution normale avec moyenne ? et variance ?-au carré. Le théorème central limite peut être résumé comme suit :

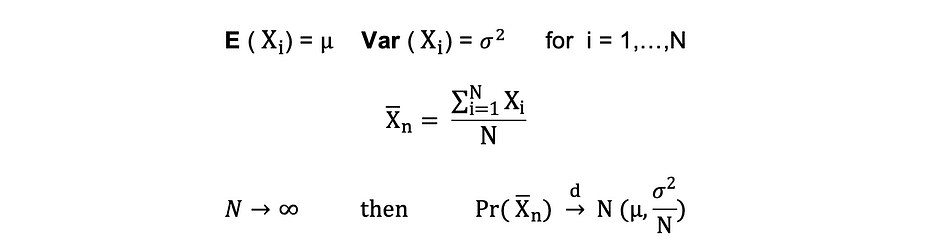
En d'autres termes, lorsque vous avez une population avec moyenne ? et écart-type ? et que vous prélevez des échantillons aléatoires suffisamment grands de cette population avec remise, la distribution des moyennes de l'échantillon sera approximativement distribuée normalement.

La réduction de la dimensionnalité est la transformation des données d'un espace de grande dimension en espace de faible dimension de telle sorte que cette représentation de faible dimension des données contienne toujours autant que possible les propriétés significatives des données d'origine.

Avec la popularité croissante du Big Data, la demande pour ces techniques de réduction de la dimensionnalité, réduisant la quantité de données et de fonctionnalités inutiles, a également augmenté. Des exemples de techniques de réduction de dimensionnalité populaires sont Analyse des composants principaux, Analyse factorielle, Corrélation canonique, Forêt aléatoire.

Analyse en composantes principales (ACP)

L'analyse en composantes principales ou PCA est une technique de réduction de la dimensionnalité qui est très souvent utilisée pour réduire la dimensionnalité de grands ensembles de données, en transformant un grand ensemble de variables en un ensemble plus petit qui contient toujours la plupart des informations ou la variation dans le grand ensemble de données d'origine. .

Supposons que nous ayons une donnée X avec p variables ; X1, X2, …., Xp avec vecteurs propres e1, …, ep, et valeurs propres ?1,…, ?p. Les valeurs propres montrent la variance expliquée par un champ de données particulier sur la variance totale. L'idée derrière l'ACP est de créer de nouvelles variables (indépendantes), appelées composantes principales, qui sont une combinaison linéaire de la variable existante. Le jeth composante principale peut être exprimée comme suit :

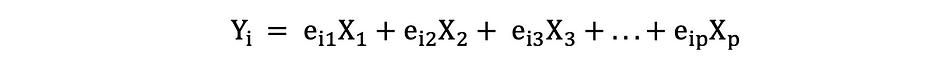
Ensuite, en utilisant Règle du coude or Règle Kaiser, vous pouvez déterminer le nombre de composants principaux qui résument de manière optimale les données sans perdre trop d'informations. Il est également important de regarder la proportion de la variation totale (PRTV) qui est expliqué par chaque composante principale pour décider s'il est avantageux de l'inclure ou de l'exclure. PRTV pour le ith la composante principale peut être calculée à l'aide des valeurs propres comme suit :

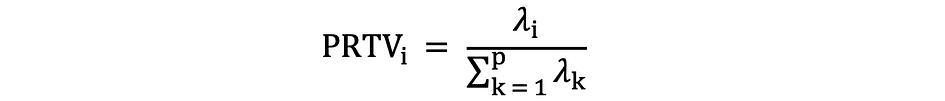
Règle du coude

La règle du coude ou la méthode du coude est une approche heuristique utilisée pour déterminer le nombre de composantes principales optimales à partir des résultats de l'ACP. L'idée derrière cette méthode est de tracer la variation expliquée en fonction du nombre de composantes et choisissez le coude de la courbe comme nombre de composantes principales optimales. Voici un exemple d'un tel nuage de points où le PRTV (axe Y) est tracé sur le nombre de composants principaux (axe X). Le coude correspond à la valeur de l'axe X 2, ce qui suggère que le nombre de composantes principales optimales est 2.

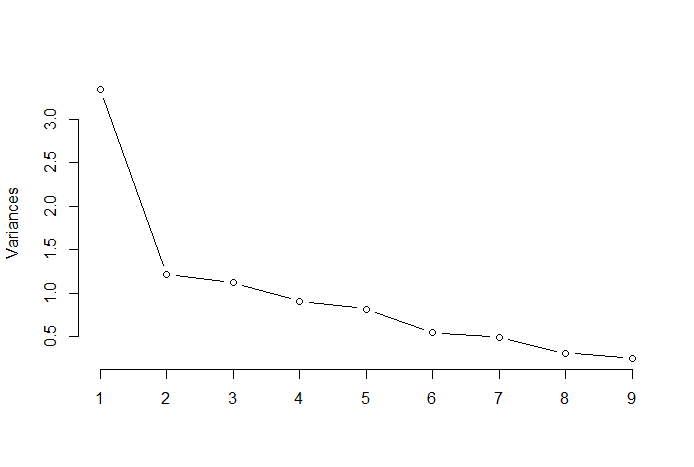
Source de l'image: Statistiques multivariées Github

Analyse factorielle (AF)

L'analyse factorielle ou FA est une autre méthode statistique de réduction de la dimensionnalité. C'est l'une des techniques d'interdépendance les plus couramment utilisées et elle est utilisée lorsque l'ensemble de variables pertinent montre une interdépendance systématique et que l'objectif est de découvrir les facteurs latents qui créent un point commun. Supposons que nous ayons une donnée X avec p variables ; X1, X2, …., Xp. Le modèle FA peut être exprimé comme suit :

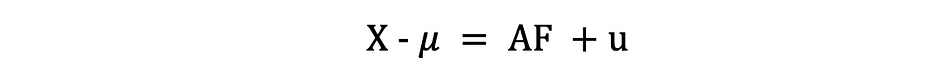
où X est une matrice [px N] de p variables et N observations, µ est [px N] matrice moyenne de la population, A est [pxk] commune matrice des saturations factorielles, F [kx N] est la matrice des facteurs communs et u [pxN] est la matrice des facteurs spécifiques. Autrement dit, un modèle factoriel est une série de régressions multiples, prédisant chacune des variables Xi à partir des valeurs des facteurs communs non observables fi :

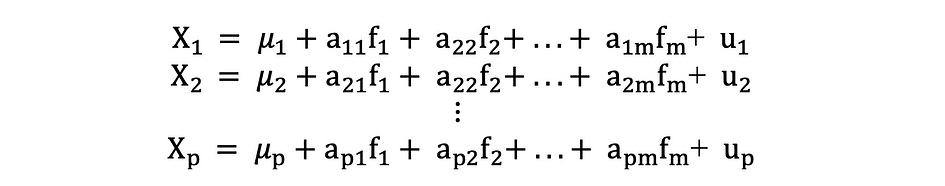
Chaque variable a k de ses propres facteurs communs, et ceux-ci sont liés aux observations via une matrice de chargement factoriel pour une seule observation comme suit : Dans l'analyse factorielle, le facteurs sont calculés à maximisent  variance entre les groupes tout en minimiser les variations intra-groupee. Ce sont des facteurs car ils regroupent les variables sous-jacentes. Contrairement à l'ACP, dans FA, les données doivent être normalisées, étant donné que FA suppose que l'ensemble de données suit la distribution normale.

 
 
Tatev Karen Aslanian est un scientifique expérimenté des données complètes, spécialisé dans l'apprentissage automatique et l'IA. Elle est également co-fondatrice de Technologie Lunaire, une plate-forme éducative technologique en ligne, et le créateur de The Ultimate Data Science Bootcamp. ses recherches scientifiques et ses articles publiés. Après cinq ans d'enseignement, Tatev canalise maintenant sa passion vers LunarTech, aidant à façonner l'avenir de la science des données.

 
ORIGINALE. Republié avec permission.
 

• Contenu propulsé par le référencement et distribution de relations publiques. Soyez amplifié aujourd'hui.
• PlatoData.Network Ai générative verticale. Autonomisez-vous. Accéder ici.
• PlatoAiStream. Intelligence Web3. Connaissance Amplifiée. Accéder ici.
• PlatonESG. Automobile / VE, Carbone, Technologie propre, Énergie, Environnement, Solaire, La gestion des déchets. Accéder ici.
• Décalages de bloc. Modernisation de la propriété des compensations environnementales. Accéder ici.
• La source: https://www.kdnuggets.com/2023/08/fundamentals-statistics-data-scientists-analysts.html?utm_source=rss&utm_medium=rss&utm_campaign=fundamentals-of-statistics-for-data-scientists-and-analysts