المُقدّمة
في هذه المقالة سوف نستكشف ما هو اختبار الفرضيات، مع التركيز على صياغة الفرضيات الصفرية والبديلة، وإعداد اختبارات الفرضيات، وسنتعمق في الاختبارات البارامترية وغير البارامترية، ومناقشة الافتراضات الخاصة بها وتنفيذها في لغة بايثون. لكن تركيزنا الأساسي سيكون على الاختبارات غير البارامترية مثل اختبار مان-ويتني يو واختبار كروسكال-واليس. في النهاية، سيكون لديك فهم شامل لاختبار الفرضيات والأدوات العملية لتطبيق هذه المفاهيم في التحليلات الإحصائية الخاصة بك.
أهداف التعلم
- فهم مبادئ اختبار الفرضيات، بما في ذلك صياغة الفرضيات الصفرية والبديلة.
- إعداد اختبار الفرضيات.
- التعرف على الاختبار البارامتري وأنواعه.
- التعرف على الاختبارات غير البارامترية وأنواعها وتطبيقاتها.
- الفرق بين البارامترية وغير البارامترية.
جدول المحتويات
ما هو اختبار الفرضيات؟
الفرضية هي ادعاء يقدمه شخص/منظمة. يتعلق الادعاء عادةً بالمعايير السكانية مثل المتوسط أو النسبة ونسعى للحصول على أدلة من عينة لدعم الادعاء.
اختبار الفرضية، والذي يشار إليه أحيانًا باسم اختبار الأهمية، هو طريقة لتأكيد ادعاء أو فرضية حول معلمة في مجتمع ما باستخدام البيانات المقاسة في العينة. باستخدام هذه الطريقة، نستكشف العديد من النظريات من خلال تحديد احتمالية اختيار عينة إحصائية لو كانت فرضية المعلمة السكانية صحيحة.
يتضمن اختبار الفرضيات صياغة فرضيتين:
- الفرضية الصفرية (H0)
- الفرضية البديلة (H1)
فرضية العدم : وهي عادةً فرضية لا يوجد بها فرق ويُشار إليها عادةً بالرمز H0. وفقًا لـ RA Fisher، فإن الفرضية الصفرية هي الفرضية التي يتم اختبارها لاحتمال رفضها على افتراض أنها صحيحة (المرجع أساسيات الإحصاء الرياضي).
فرضية بديلة: أي فرضية مكملة للفرضية الصفرية تسمى فرضية بديلة، ويشار إليها عادةً بالرمز H1.
الهدف من اختبار الفرضيات هو إما رفض الفرضية الصفرية أو الاحتفاظ بها لإنشاء علاقة ذات دلالة إحصائية بين متغيرين (عادةً متغير مستقل ومتغير تابع، أي عادةً ما يكون أحدهما هو السبب والآخر هو النتيجة).
إعداد اختبار الفرضيات
- صف الفرضية بالكلمات أو قدم ادعاءً.
- بناء على المطالبة تحديد الفرضيات الصفرية والبديلة.
- حدد نوع اختبار الفرضية المناسب للادعاء أعلاه.
- التعرف على الإحصائيات الاختبارية المستخدمة لاختبار صحة الفرضية الصفرية.
- تحديد معايير رفض الفرضية الصفرية والاحتفاظ بها. وهذا ما يسمى بقيمة الأهمية يُشار إليها تقليديًا بالرمز α (ألفا).
- احسب القيمة p التي تمثل الاحتمال الشرطي لمراقبة القيمة الإحصائية للاختبار عندما تكون الفرضية الصفرية صحيحة. بعبارات بسيطة، القيمة p هي الدليل الذي يدعم فرضية العدم.
اختبار البارامترية وغير البارامترية
لا تعتمد الاختبارات الإحصائية غير البارامترية على افتراضات حول معلمات التوزيعات السكانية التي يتم أخذ عينات منها، في حين أن الاختبارات الإحصائية البارامترية تفعل ذلك.
الاختبارات البارامترية
يتم إجراء معظم الاختبارات الإحصائية باستخدام مجموعة من الافتراضات كأساس لها. قد يؤدي التحليل إلى استنتاجات مضللة أو خاطئة تمامًا عند انتهاك بعض الافتراضات.
عادة ما تكون الافتراضات:
- الحالة الطبيعية: يتبع توزيع عينات المعلمات المراد اختبارها التوزيع الطبيعي (أو على الأقل المتماثل).
- تجانس التباينات: تباين البيانات هو نفسه عبر مجموعات مختلفة ما لم نختبر متوسطات السكان القادمة من مجموعتين مختلفتين.
بعض الاختبارات البارامترية هي:
- اختبار Z : اختبار المتوسط السكاني أو التباين أو النسبة عندما يكون الانحراف المعياري للسكان معروفا.
- اختبار الطالب: اختبار المتوسط السكاني أو التباين أو النسبة عندما يكون الانحراف المعياري للسكان غير معروف.
- اختبار t المقترن: يستخدم لمقارنة وسائل مجموعتين أو شرطين مرتبطين.
- تحليل التباين (ANOVA): يستخدم لمقارنة الوسائل عبر ثلاث مجموعات مستقلة أو أكثر.
- تحليل الانحدار: يستخدم لتقييم العلاقة بين واحد أو أكثر من المتغيرات المستقلة والمتغير التابع.
- تحليل التباين (ANCOVA): يمتد تحليل التباين (ANOVA) من خلال دمج المتغيرات المشتركة الإضافية في التحليل.
- تحليل التباين متعدد المتغيرات (MANOVA): يمتد ANOVA لتقييم الاختلافات في المتغيرات التابعة المتعددة عبر المجموعات.
الآن دعونا نتعمق في الاختبار غير البارامتري.
اختبار غير بارامترية
ولأول مرة، استخدم وولفويتز مصطلح "اللابارامترية" في عام 1942. ولكي نفهم فكرة الإحصائيات البارامترية، يتعين على المرء أولاً أن يكون لديه فهم أساسي للإحصاءات البارامترية، والتي ناقشناها للتو. أ اختبار حدودي يتطلب عينة تتبع توزيعًا محددًا (عادةً طبيعي). علاوة على ذلك، فإن الاختبارات اللابارامترية مستقلة عن الافتراضات البارامترية مثل الحالة الطبيعية.
الاختبارات غير البارامترية (تُعرف أيضًا باسم الاختبارات الحرة للتوزيع نظرًا لعدم وجود افتراضات حول توزيع السكان). تشير الاختبارات غير البارامترية إلى أن الاختبارات لا تعتمد على افتراضات مفادها أن البيانات مأخوذة من أ توزيع الاحتمالات محددة من خلال معلمات مثل المتوسط والنسبة والانحراف المعياري.
يتم استخدام الاختبارات اللامعلمية عندما:
- لا يتعلق الاختبار بالمعلمة السكانية مثل المتوسط أو النسبة.
- لا تتطلب الطريقة افتراضات حول توزيع السكان (مثل أن السكان يتبعون التوزيع الطبيعي).
أنواع الاختبارات غير البارامترية
الآن دعونا نناقش مفهوم وإجراءات إجراء اختبار Chi-Square، واختبار Mann-Whitney، واختبار Wilcoxon Signed Rank، واختبارات Kruskal-Wallis:
اختبار مربع كاي
لتحديد ما إذا كان الارتباط بين متغيرين نوعيين ذا دلالة إحصائية، يجب على المرء إجراء اختبار للأهمية يسمى اختبار Chi-Square.
هناك نوعان رئيسيان من اختبارات Chi-Square:
تشي سكوير الخير من صالح
استخدم اختبار جودة المطابقة لتحديد ما إذا كان المجتمع ذو التوزيع غير المعروف "يتناسب" مع توزيع معروف. في هذه الحالة سيكون هناك سؤال مسح نوعي واحد أو نتيجة واحدة لتجربة من مجموعة سكانية واحدة. يتم استخدام جودة الملاءمة عادةً لمعرفة ما إذا كان عدد السكان موحدًا (تحدث جميع النتائج بتكرار متساوٍ)، أو أن عدد السكان طبيعي، أو أن عدد السكان هو نفسه عدد سكان آخر بتوزيع معروف. الفرضيات الصفرية والبديلة هي:
- H0: السكان يتناسب مع التوزيع المعطى.
- Ha: عدد السكان لا يتناسب مع التوزيع المعطى.
دعونا نفهم هذا مع مثال
| يوم | الإثنين | الثلاثاء | الأربعاء | الخميس | الجمعة | السبت | الأحد |
| عدد الأعطال | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
يوضح الجدول عدد الأعطال في العامل. في هذا المثال يوجد متغير واحد فقط وعلينا تحديد ما إذا كان التوزيع الملحوظ (الوارد في الجدول) يناسب التوزيع المتوقع أم لا.
ولهذا سيتم صياغة الفرضية الصفرية والفرضية البديلة على النحو التالي:
- H0: الأعطال موزعة بشكل موحد.
- Ha: الأعطال ليست موزعة بشكل موحد.
ودرجة الحرية ستكون n-1 (في هذه الحالة n=7، لذا df = 7-1=6)
Expected value will be= (14+22+16+18+12+19+11)/7=16
| يوم | الإثنين | الثلاثاء | الأربعاء | الخميس | الجمعة | السبت | الأحد |
| عدد الأعطال (المرصودة) | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
| متوقع | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| (الملاحظ والمتوقع) | -2 | 6 | 0 | 2 | -4 | 3 | -5 |
| (الملاحظ-المتوقع)^2 | 4 | 36 | 0 | 4 | 16 | 9 | 25 |
باستخدام هذه الصيغة، قم بحساب مربع كاي
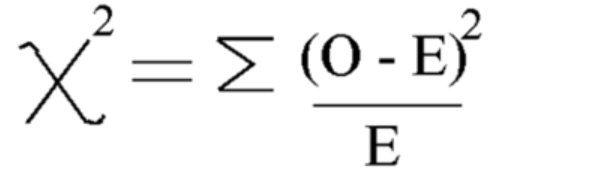
مربع كاي = 5.875
ودرجة الحرية هي = n-1=7-1=6
الآن دعونا نرى القيمة الحرجة من جدول توزيع مربع تشي عند مستوى أهمية 5%
وبالتالي فإن القيمة الحرجة هي 12.592
وبما أن القيمة المحسوبة لمربع كاي أقل من القيمة الحرجة، فإننا نقبل فرضية العدم ويمكننا أن نستنتج أن الأعطال موزعة بشكل موحد.
استقلالية مربع كاي للاختبار
استخدم اختبار الاستقلال لتحديد ما إذا كان المتغيران (العاملان) مستقلين أو تابعين، أي ما إذا كان لدى هذين المتغيرين علاقة ارتباط كبيرة بينهما أم لا. في هذه الحالة سيكون هناك سؤالين أو تجربتين للمسح النوعي وسيتم إنشاء جدول طوارئ. الهدف هو معرفة ما إذا كان المتغيران غير مرتبطين (مستقلين) أو مرتبطين (تابعين). الفرضيات الصفرية والبديلة هي:
- H0: المتغيران (العاملان) مستقلان.
- Ha: المتغيران (العوامل) يعتمدان.
لنأخذ مثالا
مثال نريد فيه التحقق مما إذا كان الجنس واللون المفضل للقميص مستقلين. هذا يعني أننا نريد معرفة ما إذا كان جنس الشخص يؤثر على اختياره للألوان. أجرينا مسحًا وقمنا بتنظيم البيانات في الجدول.
ويلاحظ هذا الجدول القيم:
| اسود | أبيض | أحمر | الأزرق | |
| شاب | 48 | 12 | 33 | 57 |
| فتاة | 34 | 46 | 42 | 26 |
الآن قم أولاً بصياغة الفرضيات الصفرية والبديلة
- H0: الجنس ولون القميص المفضل مستقلان
- Ha: الجنس ولون القميص المفضل ليسا مستقلين
لحساب إحصائيات اختبار مربع كاي، نحتاج إلى حساب القيمة المتوقعة. لذلك، أضف جميع الصفوف والأعمدة والإجماليات الإجمالية:
| اسود | أبيض | أحمر | الأزرق | الإجمالي | |
| شاب | 48 | 12 | 33 | 57 | 150 |
| فتاة | 34 | 46 | 42 | 26 | 148 |
| الإجمالي | 82 | 58 | 75 | 83 | 298 |
بعد ذلك يمكننا حساب جدول القيمة المتوقعة من الجدول أعلاه لكل مدخل باستخدام هذه الصيغة = (إجمالي الصف * إجمالي العمود) / الإجمالي الكلي
جدول القيمة المتوقعة:
| اسود | أبيض | أحمر | الأزرق | |
| شاب | 41.3 | 29.2 | 37.8 | 41.8 |
| فتاة | 40.7 | 28.8 | 37.2 | 41.2 |
الآن قم بحساب قيمة مربع كاي باستخدام صيغة اختبار مربع كاي:
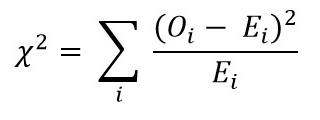
- Oi = القيمة المرصودة
- Ei = القيمة المتوقعة
القيمة التي حصلنا عليها هي: Χ2 = 34.9572
حساب درجة الحرية
DF=(عدد الصف 1)*(عدد العمود 1)
الآن ابحث عن القيمة الحرجة وقارنها باختبار مربع كاي القيمة الإحصائية:
للقيام بذلك، يمكنك البحث عن درجة الحرية ومستوى الأهمية (ألفا) من ملف جدول توزيع مربع كاي
عند ألفا = 0.050، سنحصل على القيمة الحرجة = 7.815
منذ مربع كاي> القيمة الحرجة
ولذلك، فإننا نرفض الفرضية الصفرية ويمكننا أن نستنتج أن الجنس ولون القميص المفضل ليسا مستقلين.
تنفيذ تشي سكوير
الآن، دعونا نرى تنفيذ Chi-Square باستخدام بعض الأمثلة الواقعية في لغة بايثون:
- H0: الجنس ولون القميص المفضل مستقلان
- Ha: الجنس ولون القميص المفضل ليسا مستقلين
إنشاء مجموعة البيانات:
import pandas as pd
from scipy.stats import chi2_contingency
from scipy.stats import chi2
# Given dataset
df_dict = {
'Black': [48, 34],
'White': [12, 46],
'Red': [33, 42],
'Blue': [57, 26]
}
dataset_table = pd.DataFrame(df_dict, index=['Male', 'Female'])
print("Dataset Table:")
print(dataset_table)
print()
# Observed Values
Observed_Values = dataset_table.values
print("Observed Values:")
print(Observed_Values)
print()
# Perform chi-square test
val = chi2_contingency(dataset_table)
Expected_Values = val[3]
print("Expected Values:")
print(Expected_Values)
print()
# Degree of Freedom
no_of_rows = len(dataset_table.iloc[0:2, 0])
no_of_columns = 4
ddof = (no_of_rows - 1) * (no_of_columns - 1)
print("Degree of Freedom:", ddof)
print()
# Chi-square statistic
chi_square = sum([(o - e) ** 2. / e for o, e in zip(Observed_Values, Expected_Values)])
chi_square_statistic = chi_square[0] + chi_square[1]
print("Chi-square statistic:", chi_square_statistic)
print()
# Critical value
alpha = 0.05
critical_value = chi2.ppf(q=1-alpha, df=ddof)
print('Critical value:', critical_value)
print()
# p-value
p_value = 1 - chi2.cdf(x=chi_square_statistic, df=ddof)
print('p-value:', p_value)
print()
# Significance level
print('Significance level:', alpha)
print('p-value:', p_value)
print('Degree of Freedom:', ddof)
print()
# Hypothesis testing
if chi_square_statistic >= critical_value:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
print()
if p_value <= alpha:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
الإخراج:
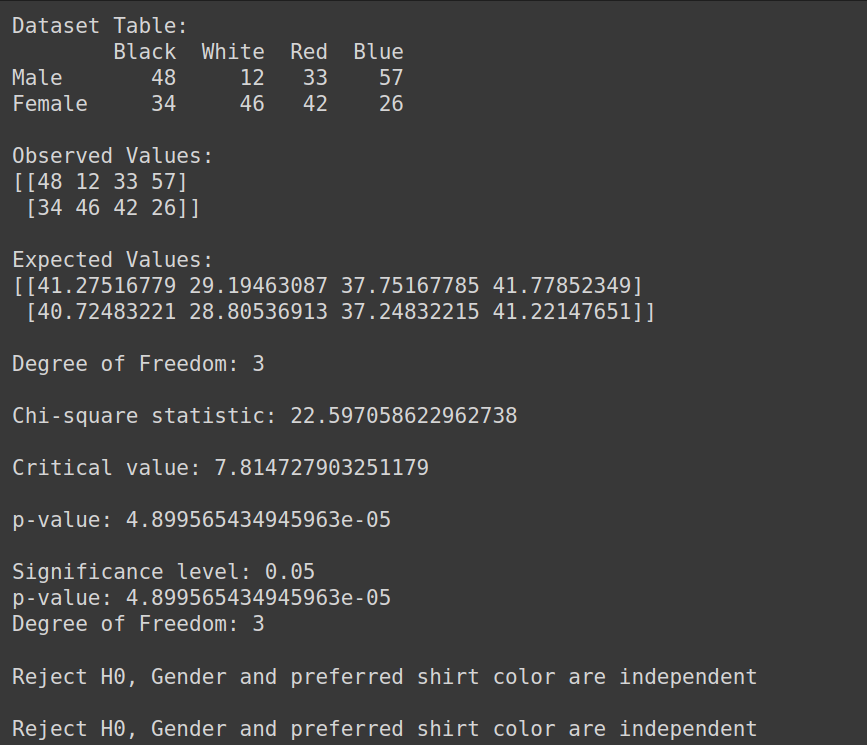
اختبار مان ويتني يو
يعد اختبار مان ويتني يو بمثابة البديل غير البارامتري لاختبار t للعينة المستقلة. وهو يقارن بين متوسطي عينة من نفس المجتمع، ويحدد ما إذا كانا متساويين. يُستخدم هذا الاختبار عادةً للبيانات الترتيبية أو عندما لا يتم استيفاء افتراضات اختبار t.
يقوم اختبار مان ويتني يو بتصنيف جميع القيم من كلا المجموعتين معًا، ثم يجمع الرتب لكل مجموعة. يقوم بحساب إحصائية الاختبار، U، بناءً على هذه الرتب. تتم مقارنة إحصائية U بقيمة حرجة من جدول أو يتم حسابها باستخدام طريقة تقريبية. إذا كانت إحصائية U أقل من القيمة الحرجة، فسيتم رفض فرضية العدم.
وهذا يختلف عن الاختبارات البارامترية مثل اختبار t، الذي يقارن المتوسطات ويفترض التوزيع الطبيعي. بدلاً من ذلك، يقارن اختبار مان-ويتني يو الرتب ولا يتطلب افتراض التوزيع الطبيعي.
قد يكون فهم اختبار مان ويتني يو أمرًا صعبًا لأن النتائج يتم عرضها في اختلافات رتبة المجموعة بدلاً من اختلافات متوسط المجموعة.
صيغة اختبار مان ويتني:
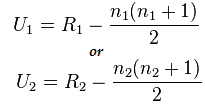
U = دقيقة (U1، U2)
هنا،
- U = اختبار مان ويتني U
- n1 = حجم العينة واحد
- n2= حجم العينة الثاني
- R1= ترتيب حجم العينة واحد
- R2= ترتيب حجم العينة 2
لذا، دعونا نفهم هذا بمثال قصير:
لنفترض أننا نريد مقارنة فعالية طريقتين علاجيتين مختلفتين (الطريقة أ والطريقة ب) في تحسين صحة المرضى. لدينا البيانات التالية:
- الطريقة أ: 3,4,2,6,2,5،XNUMX،XNUMX،XNUMX،XNUMX،XNUMX
- الطريقة ب: 9,7,5,10,6,8،XNUMX،XNUMX،XNUMX،XNUMX،XNUMX
وهنا، يمكننا أن نرى أن البيانات لا يتم توزيعها بشكل طبيعي، وأن أحجام العينات صغيرة.
تنفيذ اختبار مان ويتني يو
والآن لنجري اختبار مان-ويتني يو:
لكن دعونا أولاً نقوم بصياغة الفرضية الصفرية والبديلة
- H0: لا يوجد فرق بين رتبة كل معاملة
- Ha: هناك فرق بين رتبة كل معاملة
الجمع بين جميع العلاجات: 3,4,2,6,2,5,9,7,5,10,6,8،XNUMX،XNUMX،XNUMX،XNUMX،XNUMX،XNUMX،XNUMX،XNUMX،XNUMX،XNUMX،XNUMX
البيانات المصنفة: 2,2,3,4,5,5,6,6,7,8,9,10
ترتيب البيانات المصنفة: 1,2,3,4,5,6,7,8,9,10,11,12
- ترتيب البيانات بشكل منفصل:
- Method A: 3(3),4(4),2(1.5),6(7.5),2(1.5),5(5.5)
- Method B: 9(11),7(9),5(5.5),10(12),6(1.5),8(10)
- حساب مجموع الرتبة):
- R1: 3+4+1.5+7.5+1.5+5.5=23
- R2: 11+9+5.5+12+1.5+10=55
الآن احسب القيمة الإحصائية باستخدام هذه الصيغة:
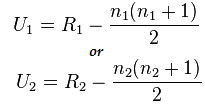
هنا n1=6 و n2=6
والقيمة بعد الحساب لـ U1=2 وU2= 34
حساب إحصائية U :
نحن = دقيقة (U1، U2) = دقيقة (2,34،2) = XNUMX
من طاولة مان ويتني يمكننا العثور على القيمة الحرجة
في هذه الحالة ستكون القيمة الحرجة 5
وبما أن Uc= 5 وهي أكبر منا عند مستوى معنوية 5%، فإننا نرفض H0
ومن هنا يمكننا أن نستنتج أن هناك فرقا بين رتبة كل معاملة.
التنفيذ مع بايثون
from scipy.stats import mannwhitneyu, norm
import numpy as np
TreatmentA = np.array([3,4,2,6,2,5])
TreatmentB = np.array([9,7,5,10,6,8])
# Perform Mann-Whitney U test
U_statistic, p_value = mannwhitneyu(TreatmentA, TreatmentB)
# Print the result
print(f'The U-statistic is {U_statistic:.2f} and the p-value is {p_value:.4f}')
if p_value < 0.05:
print("Reject Null Hypothesis: There is a significant difference between the Rank of each treatment.")
else:
print("Fail to Reject Null Hypothesis: Fail to Reject Null Hypothesis: There is no enough evidence to conclude that there is difference between the Rank of each treatment")الإخراج:

اختبار كروسكال-واليس
يُستخدم اختبار كروسكال-واليس مع مجموعات متعددة. إنه بديل غير معلمي وقيم لاختبار ANOVA أحادي الاتجاه عند انتهاك الحالة الطبيعية والمساواة في افتراضات التباين. اختبار كروسكال – واليس يقارن متوسطات أكثر من مجموعتين مستقلتين.
إنه يختبر الفرضية الصفرية عندما يتم سحب عينات مستقلة k (k>=3) من مجموعة سكانية ذات توزيعات متطابقة، دون الحاجة إلى شرط الحالة الطبيعية للسكان.
الافتراضات:
تأكد من وجود ثلاث عينات عشوائية على الأقل تم سحبها بشكل مستقل. تحتوي كل عينة على 5 ملاحظات على الأقل، n>=5
فكر في مثال حيث نريد تحديد ما إذا كانت تقنية الدراسة التي تستخدمها ثلاث مجموعات من الطلاب تؤثر على درجات امتحاناتهم. يمكننا استخدام اختبار كروسكال واليس لتحليل البيانات وتقييم ما إذا كانت هناك فروق ذات دلالة إحصائية في درجات الامتحانات بين المجموعات.
صياغة الفرضية الصفرية لذلك على النحو التالي:
- H0: لا يوجد اختلاف في درجات الامتحان بين المجموعات الثلاث من الطلاب.
- Ha: هناك اختلاف في درجات الامتحان بين المجموعات الثلاث من الطلاب.
اختبار رتبة ويلكوكسون الموقّع
اختبار تصنيف ويلكوكسون الموقع (المعروف أيضًا باسم اختبار ويلكوكسون للزوج المتطابق) هو النسخة غير البارامترية لاختبار t للعينة التابعة أو اختبار t للعينة المقترنة. اختبار الإشارة هو البديل اللامعلمي الآخر لاختبار t للعينة المقترنة. يتم استخدامه عندما تكون المتغيرات محل الاهتمام ثنائية بطبيعتها (مثل ذكر وأنثى، نعم ولا). يعد اختبار رتبة ويلكوكسون الموقع أيضًا إصدارًا غير معلمي لعينة واحدة من اختبار t. يقارن اختبار التصنيف الموقع لويلكوكسون متوسطات المجموعات في حالتين (عينات مقترنة) أو يقارن متوسط المجموعة مع المتوسط المفترض (عينة واحدة).
دعونا نفهم ذلك بمثال لنفترض أن لدينا بيانات عن استهلاك السجائر اليومي للمدخنين قبل وبعد المشاركة في برنامج مدته 8 أسابيع، ونريد تحديد ما إذا كان هناك فرق كبير في استهلاك السجائر اليومي قبل وبعد البرنامج، فسنقوم بذلك استخدم هذا الاختبار
وستكون صياغة الفرضية لهذا
- H0: لا يوجد فرق في استهلاك السجائر اليومي قبل البرنامج وبعده.
- Ha: هناك اختلاف في استهلاك السجائر اليومي قبل البرنامج وبعده
اختبار للحياة الطبيعية
دعونا الآن نناقش اختبارات الحالة الطبيعية:
اختبار شابيرو ويلك
يقوم اختبار شابيرو ويلك بتقييم ما إذا كانت عينة معينة من البيانات تأتي من مجموعة سكانية موزعة بشكل طبيعي. إنه أحد الاختبارات الأكثر استخدامًا للتحقق من الحالة الطبيعية. ويكون الاختبار مفيدًا بشكل خاص عند التعامل مع عينات ذات أحجام صغيرة نسبيًا.
في اختبار شابيرو ويلك:
- فرضية العدم : تأتي بيانات العينة من مجتمع يتبع التوزيع الطبيعي.
- فرضية بديلة : لا تأتي بيانات العينة من مجتمع يتبع التوزيع الطبيعي.
تقيس إحصائية الاختبار الناتجة عن اختبار شابيرو-ويلك التناقض بين البيانات المرصودة والبيانات المتوقعة في ظل افتراض الحالة الطبيعية. إذا كانت القيمة p المرتبطة بإحصائيات الاختبار أقل من مستوى الأهمية المختار (على سبيل المثال، 0.05)، فإننا نرفض فرضية العدم، مما يشير إلى أن البيانات لا يتم توزيعها بشكل طبيعي. إذا كانت القيمة p أكبر من مستوى الأهمية، فإننا نفشل في رفض فرضية العدم، مما يشير إلى أن البيانات قد تتبع التوزيع الطبيعي.
أولاً لنقم بإنشاء مجموعة بيانات لهذه الاختبارات، يمكنك استخدام أي مجموعة بيانات من اختيارك:
import pandas as pd
# Create the dictionary with the provided data
data = {
'population': [6.1101, 5.5277, 8.5186, 7.0032, 5.8598],
'profit': [17.5920, 9.1302, 13.6620, 11.8540, 6.8233]
}
# Create the DataFrame
df = pd.DataFrame(data)
response_var=df['profit']
Here, a sample for running Shapiro -Wilk test on python:
from scipy.stats import shapiro
stat, p_val = shapiro(response_var)
print(f'Shapiro-Wilk Test: Statistic={stat} p-value={p_val}')
if p_val > alpha:
print('Data looks normal (fail to reject H0)')
else:
print('Data looks normal (fail to reject H0)')الإخراج:

يعد هذا الاختبار أكثر ملاءمة لأحجام العينات الصغيرة نسبيًا (n = <50-2000) حيث يصبح أقل موثوقية مع أحجام العينات الأكبر.
أندرسون دارلينج
وهو يقيم ما إذا كانت عينة معينة من البيانات تأتي من توزيع محدد، مثل التوزيع الطبيعي. إنه مشابه لاختبار شابيرو ويلك ولكنه أكثر حساسية خاصة بالنسبة لأحجام العينات الأصغر.
يناسب عدة توزيعات، بما في ذلك التوزيع الطبيعي، في الحالات التي تكون فيها معلمات التوزيع غير معروفة.
هنا كود بايثون لتنفيذه:
from scipy.stats import anderson
response_var = data['profit']
alpha = 0.05
# Anderson-Darling Test
result = anderson(response_var)
print(f'Anderson statistics: {result.statistic:.3f}')
if result.statistic > result.critical_values[-1]:
p_value = 0.0 # The p-value is essentially 0 if the statistic exceeds the largest critical value
else:
p_value = result.significance_level[result.statistic < result.critical_values][-1]
print("P-value:", p_value)
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")الإخراج:

اختبار جارك بيرا
يقوم اختبار Jarque-Bera بتقييم ما إذا كانت عينة معينة من البيانات تأتي من مجموعة سكانية موزعة بشكل طبيعي. يعتمد على انحراف البيانات وتفرطحها.
فيما يلي تنفيذ اختبار Jarque-Bera في Python مع بيانات نموذجية:
from scipy.stats import jarque_bera
# Performing Jarque-Bera test
test_statistic, p_value = jarque_bera(response_var)
print("Jarque-Bera Test Statistic:", test_statistic)
print("P-value:", p_value)
# Interpreting results
alpha = 0.05
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")الإخراج:

| الفئة | التقنيات الإحصائية البارامترية | الإحصائية غير البارامتريةتقنيات |
| ارتباط | معامل بيرسون العزمي للارتباط (ص) | معامل ارتباط رتبة سبيرمان (Rho)، كيندال تاو |
| مجموعتان، تدابير مستقلة | اختبار t المستقل | اختبار مان ويتني يو |
| أكثر من مجموعتين، تدابير مستقلة | اتجاه واحد أنوفا | كروسكال واليس طريقة واحدة ANOVA |
| مجموعتين، والتدابير المتكررة | اختبار t المقترن | اختبار رتبة الزوج المطابق لويلكوكسون |
| أكثر من مجموعتين، التدابير المتكررة | في اتجاه واحد، تدابير متكررة ANOVA | تحليل التباين الثنائي لفريدمان |
وفي الختام
اختبار الفرضيات يعد ضروريًا لتقييم المطالبات المتعلقة بالمعلمات السكانية باستخدام بيانات العينة. تعتمد الاختبارات البارامترية على افتراضات محددة وهي مناسبة للبيانات الفاصلة أو النسبية، في حين أن الاختبارات غير البارامترية أكثر مرونة وقابلة للتطبيق على البيانات الاسمية أو الترتيبية دون افتراضات توزيعية صارمة. اختبارات مثل شابيرو ويلك وأندرسون دارلينج تقيم الحالة الطبيعية، في حين أن تشي سكوير وجارك بيرا تقيم مدى جودة اللياقة. يعد فهم الاختلافات بين الاختبارات البارامترية وغير البارامترية أمرًا بالغ الأهمية لاختيار النهج الإحصائي المناسب. بشكل عام، يوفر اختبار الفرضيات إطارًا منهجيًا لاتخاذ القرارات المستندة إلى البيانات واستخلاص استنتاجات موثوقة من الأدلة التجريبية.
هل أنت مستعد لإتقان التحليل الإحصائي المتقدم؟ قم بالتسجيل في دورة تحليل بيانات BlackBelt اليوم! اكتسب الخبرة في اختبار الفرضيات، والاختبارات البارامترية وغير البارامترية، وتنفيذ بايثون، والمزيد. ارفع مهاراتك الإحصائية وتفوق في اتخاذ القرارات المستندة إلى البيانات. نضم الان!
الأسئلة المتكررة
أ- الاختبارات البارامترية تضع افتراضات حول توزيع المجتمع ومعاييره، مثل الحالة الطبيعية وتجانس التباين، في حين أن الاختبارات غير البارامترية لا تعتمد على هذه الافتراضات. تتمتع الاختبارات البارامترية بقوة أكبر عند استيفاء الافتراضات، في حين تكون الاختبارات غير البارامترية أكثر قوة وقابلة للتطبيق في نطاق أوسع من المواقف، بما في ذلك عندما تكون البيانات منحرفة أو غير موزعة بشكل طبيعي.
أ. يتم استخدام اختبار مربع كاي لتحديد ما إذا كان هناك ارتباط كبير بين متغيرين فئويين. يقوم عادةً بتحليل البيانات الفئوية واختبار الفرضيات حول استقلالية المتغيرات في جداول الطوارئ.
أ. يقارن اختبار مان ويتني يو مجموعتين مستقلتين عندما يكون المتغير التابع ترتيبيًا أو غير موزع بشكل طبيعي. ويقيم ما إذا كان هناك فرق كبير بين متوسطات المجموعتين.
ج: يقوم اختبار شابيرو-ويلك بتقييم ما إذا كانت العينة تأتي من مجموعة سكانية موزعة بشكل طبيعي. إنه يختبر الفرضية الصفرية القائلة بأن البيانات تتبع التوزيع الطبيعي. إذا كانت القيمة p أقل من مستوى الأهمية المختار (على سبيل المثال، 0.05)، فإننا نرفض فرضية العدم، ونستنتج أن البيانات لا يتم توزيعها بشكل طبيعي.
- محتوى مدعوم من تحسين محركات البحث وتوزيع العلاقات العامة. تضخيم اليوم.
- PlatoData.Network Vertical Generative Ai. تمكين نفسك. الوصول هنا.
- أفلاطونايستريم. ذكاء Web3. تضخيم المعرفة. الوصول هنا.
- أفلاطون كربون، كلينتك ، الطاقة، بيئة، شمسي، إدارة المخلفات. الوصول هنا.
- أفلاطون هيلث. التكنولوجيا الحيوية وذكاء التجارب السريرية. الوصول هنا.
- المصدر https://www.analyticsvidhya.com/blog/2024/04/a-comprehensive-guide-on-non-parametric-tests/



