Vitalik Buterin aracılığıyla Vitalik Buterin'in Blogu
Bu, şu adresteki yazının bir aynasıdır: https://medium.com/@VitalikButerin/exploring-eliptic-curve-pairings-c73c1864e627
Tetikleyici uyarı: matematik.
Deterministik eşik imzaları, zk-SNARK'lar ve sıfır bilgi kanıtlarının diğer basit biçimleri de dahil olmak üzere çeşitli yapıların arkasındaki temel kriptografik ilkelerden biri eliptik eğri eşleştirmesidir. Eliptik eğri eşleştirmeleri (veya "çift doğrusal haritalar"), şifreleme ve dijital imzalar da dahil olmak üzere kriptografik uygulamalar için eliptik eğrilerin kullanıldığı 30 yıllık geçmişe yeni eklenen bir şeydir; eşleştirmeler, eliptik eğri tabanlı protokollerin yapabileceklerini büyük ölçüde genişleten bir "şifreli çarpma" biçimi sunar. Bu makalenin amacı eliptik eğri eşleştirmelerini ayrıntılı olarak ele almak ve nasıl çalıştıklarına dair genel bir taslak açıklamak olacaktır.
İlk okuduğunuzda, hatta onuncu okuyuşunuzda bile buradaki her şeyi anlamanız beklenmiyor; bu işler gerçekten zordur. Ancak umarım bu makale size en azından kaputun altında neler olup bittiğine dair bir fikir verecektir.
Eliptik eğrilerin kendisi de anlaşılması kolay olmayan bir konudur ve bu makale genel olarak onların nasıl çalıştığını bildiğinizi varsayacaktır; Bunu yapmazsanız, buradaki makaleyi bir başlangıç olarak öneririm: https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/. Kısa bir özet olarak, eliptik eğri kriptografisi, bunları eklemek ve çıkarmak için (örn. �= koordinatlarını hesaplamak için) özel formüllerle birlikte "noktalar" adı verilen matematiksel nesneleri (bunlar (�,�) koordinatları olan gerçek iki boyutlu noktalardır) içerir. �+�) ve aynı zamanda bir noktayı bir tam sayıyla da çarpabilirsiniz (örn. �⋅�=�+�+…+�, ancak � büyükse bunu hesaplamanın çok daha hızlı bir yolu vardır).
Nokta aritmetiğinde sıfırın karşılığı olan “sonsuzdaki nokta” (�) adı verilen özel bir nokta vardır; �+�=� her zaman böyledir. Ayrıca bir eğrinin “sipariş“; herhangi bir � için �⋅�=� olacak şekilde bir � sayısı vardır (ve tabii ki �⋅(�+1)=�,�⋅(7⋅�+5)=�⋅5, vb.). Ayrıca, bir anlamda 1 sayısını temsil ettiği anlaşılan, üzerinde genel olarak mutabakata varılan bazı "üreteç noktası" da vardır. Teorik olarak, bir eğri üzerindeki herhangi bir nokta (� hariç) � olabilir; Önemli olan tek şey ��'nin standartlaştırılmış olmasıdır.
Eşleştirmeler bir adım daha ileri giderek eliptik eğri noktalarındaki daha karmaşık bazı denklem türlerini kontrol etmenize olanak sağlar; örneğin, �=�⋅�,�=�⋅� ve �=�⋅� ise, olup olmadığını veya olup olmadığını kontrol edebilirsiniz. �⋅�=� değil, girdi olarak yalnızca �,� ve � bulunur. Bu, eliptik eğrilerin temel güvenlik garantilerinin ihlal edildiği gibi görünebilir, çünkü � hakkındaki bilgiler sadece P'yi bilmekten sızıyor, ancak sızıntının oldukça kontrol altına alındığı ortaya çıkıyor - özellikle de kararsal Diffie Hellman problemi kolaydır, ancak hesaplamalı Diffie Hellman problemi (yukarıdaki örnekte � ve �'yi bilmek, bilgisayar �=�⋅�⋅�) ve ayrık logaritma problemi (�'yi �'den kurtarmak) hesaplama açısından olanaksız kalır (en azından daha önce olsaydı).
Eşleştirmelerin ne işe yaradığına bakmanın üçüncü bir yolu ve ele aldığımız çoğu kullanım durumu için belki de en aydınlatıcı olanı, eliptik eğri noktalarını tek yönlü şifrelenmiş sayılar (yani, ����) olarak görmenizdir. ����(�)=�⋅�=�), oysa geleneksel eliptik eğri matematiği kontrol etmenizi sağlar doğrusal sayılar üzerindeki kısıtlamalar (örn. eğer �=�⋅�,�=�⋅� ve �=�⋅� ise, 5⋅�+7⋅�=11⋅� kontrol etmek Gerçekten mi 5⋅�+7⋅�=11⋅� olduğunu kontrol ederek), eşleştirmeler kontrol etmenizi sağlar ikinci dereceden kısıtlamalar (örn. �(�,�)⋅�(�,�⋅5)=1 öğesinin kontrol edilmesi Gerçekten mi kontrol ediyorum: ⋅�+5=0). Ve ikinci dereceden sisteme geçmek, deterministik eşik işaretleri, ikinci dereceden aritmetik programlar ve diğer tüm güzel şeylerle çalışmamıza izin vermek için yeterlidir.
Peki yukarıda tanıttığımız bu komik `(�,�) operatörü nedir? Bu eşleşmedir. Matematikçiler bazen buna "a" da derler. çift doğrusal harita; Buradaki "çift doğrusal" kelimesi temel olarak kısıtlamaları karşıladığı anlamına gelir:
�(�,�+�)=�(�,�)⋅�(�,�)
�(�+�,�)=�(�,�)⋅�(�,�)
+ ve ⋅'un isteğe bağlı operatörler olabileceğini unutmayın; yeni ve şık matematiksel nesneler yaratırken soyut cebir + ve ⋅'un nasıl olduğunu umursamaz tanımlı, olağan yollarla tutarlı oldukları sürece, örn. �+�=�+�,(�⋅�)⋅�=�⋅(�⋅�) ve (�⋅�)+(�⋅�)=(�+�)⋅�.
�, �, � ve � basit olsaydı sayılar, o zaman basit bir eşleştirme yapmak kolaydır: �(�,�)=2�� işlemini yapabiliriz. O zaman şunları görebiliriz:
�(3,4+5)=23⋅9=227
�(3,4)⋅�(3,5)=23⋅4⋅23⋅5=212⋅215=227
Çift doğrusaldır!
Ancak bu tür basit eşleştirmeler kriptografiye uygun değildir çünkü üzerinde çalıştıkları nesneler basit tamsayılardır ve analiz edilmesi çok kolaydır; tamsayılar bölmeyi, logaritmayı hesaplamayı ve diğer çeşitli hesaplamaları kolaylaştırır; basit tam sayıların "genel anahtar" veya "tek yönlü işlev" kavramı yoktur. Ek olarak, yukarıda açıklanan eşleştirmeyle geriye doğru gidebilirsiniz - �'yi bilerek ve �(�,�)'yi bilerek, �'yi belirlemek için basitçe bir bölme ve logaritma hesaplayabilirsiniz. Toplayabileceğiniz, çıkarabileceğiniz, çarpabileceğiniz ve bölebileceğiniz “kara kutulara” mümkün olduğunca yakın matematiksel nesneler istiyoruz, ama başka bir şey yapma. Eliptik eğrilerin ve eliptik eğri eşleşmelerinin devreye girdiği yer burasıdır.
Eliptik eğri noktaları üzerinde çift doğrusal bir harita yapmanın mümkün olduğu ortaya çıktı; yani, � ve � girdilerinin eliptik eğri noktaları olduğu ve çıktının bir olduğu bir �(�,�) fonksiyonu bulmanın mümkün olduğu ortaya çıktı. (��)12 elemanı (en azından burada ele alacağımız özel durumda; ayrıntılar eğrinin ayrıntılarına bağlı olarak farklılık gösterir, buna daha sonra değineceğiz), ancak bunu yapmanın arkasındaki matematik oldukça karmaşıktır.
Öncelikle asal alanları ve uzantı alanlarını ele alalım. Bu yazının başındaki resimdeki oldukça eliptik eğri, yalnızca eğri denkleminin normal gerçek sayılar kullanılarak tanımlandığını varsayarsanız bu şekilde görünür. Bununla birlikte, kriptografide gerçekten normal gerçek sayıları kullanırsak, o zaman "geriye gitmek" için logaritma kullanabilirsiniz ve her şey bozulur; ayrıca sayıları gerçekten depolamak ve temsil etmek için gereken alan miktarı keyfi olarak artabilir. Bu nedenle, bunun yerine sayıları kullanıyoruz asal alan.
Bir asal alan, �'nin asal olduğu 0,1,2…�−1 sayı kümesinden oluşur ve çeşitli işlemler aşağıdaki gibi tanımlanır:
�+�:(�+�) % �
�⋅�:(�⋅�) % �
�−�:(�−�) % �
�/�:(�⋅��−2) % �
Temel olarak tüm matematik modülo olarak yapılır (bkz. okuyun Modüler matematiğe giriş için). Bölünme özel bir durumdur; normalde 32 bir tam sayı değildir ve burada yalnızca tam sayılarla uğraşmak istiyoruz, dolayısıyla bunun yerine �⋅2=3 olacak şekilde � sayısını bulmaya çalışıyoruz; burada ⋅ elbette yukarıda tanımlandığı gibi modüler çarpmayı ifade ediyor. Sayesinde Fermat'ın küçük teoremiyukarıda gösterilen üstel alma numarası işi yapar, ancak bunu yapmanın daha hızlı bir yolu da vardır: Genişletilmiş Öklid Algoritması. Diyelim ki �=7; işte birkaç örnek:
2+3=5 % 7=5
4+6=10 % 7=3
2−5=−3 % 7=4
6⋅3=18 % 7=4
3/2=(3⋅25) % 7=5
5⋅2=10 % 7=3
Bu tür bir matematikle biraz oynarsanız, bunun son derece tutarlı olduğunu ve tüm olağan kuralları karşıladığını fark edeceksiniz. Yukarıdaki son iki örnekte (�/�)⋅�=�; ayrıca (�+�)+�=�+(�+�),(�+�)⋅�=�⋅�+�⋅� olduğunu ve bildiğiniz ve sevdiğiniz diğer tüm lise cebirsel kimliklerinin devam ettiğini de görebilirsiniz. aynı zamanda doğru tutmak için. Gerçekte eliptik eğrilerde noktalar ve denklemler genellikle asal alanlarda hesaplanır.
Şimdi konuşalım uzatma alanları. Muhtemelen daha önce bir uzantı alanı görmüşsünüzdür; Matematik ders kitaplarında karşılaştığınız en yaygın örnek, gerçek sayılar alanının −1=� ek öğesiyle "genişletildiği" karmaşık sayılar alanıdır. Temel olarak, uzantı alanları mevcut bir alanı alıp ardından yeni bir öğe "icat ederek" ve bu öğe ile mevcut öğeler arasındaki ilişkiyi tanımlayarak (bu durumda, -2+1=0) ve bu denklemin doğru olmadığından emin olarak çalışır. orijinal alandaki herhangi bir sayı için ve orijinal alanın elemanlarının ve yeni oluşturduğunuz yeni elemanın tüm doğrusal kombinasyonlarının kümesine bakmak.

(2+3�)+(4+2�)=6+5�
(5+2�)+3=1+2�
(6+2�)⋅2=5+4�
4�⋅(2+�)=3+�
Bu son sonucu anlamak biraz zor olabilir; orada olan şey şuydu, önce çarpımı 4 bölü 2+4 bölü ⋅'ye ayrıştırdık, bu da 8 bölü 4'ü verir ve sonra mod7 matematiğiyle çalıştığımız için �+3 olur. Bölmek için şunu yaparız:
�/�:(�⋅�(�2−2)) % �
Fermat'ın küçük teoreminin üssünün artık � yerine �2 olduğuna dikkat edin, ancak bir kez daha daha verimli olmak istiyorsak bunun yerine Genişletilmiş Öklid Algoritmasını işi yapacak şekilde genişletebiliriz. Bu alandaki herhangi bir � için ��2−1=1 olduğuna dikkat edin, dolayısıyla �2−1’e “alandaki çarpımsal grubun sırası” diyoruz.
Gerçek sayılarla, Cebirin Temel Teoremi Karmaşık sayılar olarak adlandırdığımız ikinci dereceden genişlemenin "tam" olmasını sağlar - bunu daha fazla genişletemezsiniz, çünkü herhangi bir matematiksel ilişki için (en azından cebirsel bir formülle tanımlanan herhangi bir matematiksel ilişki için) bazı yeni öğeler arasında bulabilirsiniz. ve mevcut karmaşık sayılar arasında, bu ilişkiyi zaten karşılayan en az bir karmaşık sayı bulmak mümkündür. Ancak asal alanlarda bu sorunu yaşamıyoruz ve bu nedenle daha da ileri gidip kübik genişletmeler yapabiliriz (burada bazı yeni elementler ile mevcut alan elemanları arasındaki matematiksel ilişki kübik bir denklemdir, yani 1,' ve σ2 eşittir) tümü birbirinden doğrusal olarak bağımsızdır), yüksek dereceli uzantılar, uzantıların uzantıları vb. Ve eliptik eğri eşleştirmelerinin üzerine inşa edildiği şey, bu tür süper yüklü modüler karmaşık sayılardır.
Tüm bu işlemlerin kodla yazılmasıyla ilgili tam matematiği görmek isteyenler için asal alanlar ve alan uzantıları burada uygulanmaktadır: https://github.com/ethereum/py_pairing/blob/master/py_ecc/bn128/bn128_field_elements.py
Şimdi eliptik eğri eşleştirmelerine geçelim. Eliptik bir eğri eşleşmesi (veya daha doğrusu, burada keşfedeceğimiz özel eşleştirme biçimi; mantıkları oldukça benzer olmasına rağmen başka türde eşleştirmeler de vardır) bir �2×�1→�� haritasıdır, burada:
- �1 eliptik bir eğridir; burada noktalar �2=�3+� formundaki bir denklemi karşılar ve her iki koordinat da ��'nin elemanlarıdır (yani bunlar basit sayılardır, ancak aritmetiğin tümü bir asal sayının modulo'su olarak yapılır)
- �2 eliptik bir eğridir; burada noktalar �1 ile aynı denklemi sağlar, ancak koordinatların (��)12'nin elemanları olması dışında (yani yukarıda bahsettiğimiz aşırı yüklü karmaşık sayılardır; yeni bir "sihirli sayı" tanımlarız) ” �, �12−12⋅�18+6=82 gibi 0. dereceden bir polinomla tanımlanır)
- �� eliptik eğrinin sonucunun gireceği nesne türüdür. Baktığımız eğrilerde �� (��)12’dir (�2’de kullanılan aşırı yüklü karmaşık sayının aynısı)
Karşılaması gereken ana özellik çift doğrusallıktır ve bu bağlamda bu şu anlama gelir:
- �(�,�+�)=�(�,�)⋅�(�,�)
- �(�+�,�)=�(�,�)⋅�(�,�)
İki önemli kriter daha var:
- Verimli hesaplanabilirlik (örneğin, tüm noktaların ayrık logaritmasını alıp bunları birbiriyle çarparak kolay bir eşleştirme yapabiliriz, ancak bu, ilk etapta eliptik eğri kriptografisini kırmak kadar hesaplama açısından zordur, dolayısıyla sayılmaz)
- Dejenerasyon olmaması (elbette, yalnızca �(�,�)=1 tanımlayabilirsiniz, ancak bu pek kullanışlı bir eşleştirme değildir)
Peki bunu nasıl yapacağız?
Eşleştirme fonksiyonlarının neden çalıştığının ardındaki matematik oldukça çetrefilli ve şu ana kadar gördüklerimizin ötesine geçen oldukça ileri düzey cebir içeriyor, ancak bunun bir taslağını sunacağım. Öncelikle kavramı tanımlamamız gerekiyor. bölentemel olarak eliptik eğri noktalarında fonksiyonları temsil etmenin alternatif bir yoludur. Bir fonksiyonun böleni temel olarak fonksiyonun sıfırlarını ve sonsuzluklarını sayar. Bunun ne anlama geldiğini anlamak için birkaç örnek üzerinden gidelim. Bir �=(��,��) noktasını sabitleyelim ve aşağıdaki fonksiyonu ele alalım:
�(�,�)=�−��
Bölen [�]+[−�]−2⋅[�]'dir (köşeli parantezler bahsettiğimiz gerçeği temsil etmek için kullanılır fonksiyonun sıfırlar ve sonsuzluklar kümesinde � noktasının varlığı, P noktasının kendisi değil; [�]+[�] şu şekildedir: değil [�+�] ile aynı şeydir). Gerekçe şu şekilde:
- Fonksiyon � noktasında sıfıra eşittir, çünkü � is ��, yani �−��=0
- −� ve � aynı � koordinatını paylaştığından fonksiyon −� noktasında sıfıra eşittir
- � sonsuza giderken fonksiyon da sonsuza gider, dolayısıyla fonksiyonun � noktasında sonsuza eşit olduğunu söyleriz. Bu sonsuzluğun iki kez sayılmasının teknik bir nedeni vardır, bu nedenle -2 "çokluğu" ile eklenir (negatif çünkü sıfır değil bir sonsuzluktur, bu çift sayma nedeniyle iki).
Teknik sebep kabaca şudur: Eğrinin denklemi �3=�2+� olduğundan,� �1.5'nin �2'e yetişmesi için �'den "3 kat daha hızlı" sonsuza gider; dolayısıyla, eğer doğrusal bir fonksiyon yalnızca � içeriyorsa o zaman 2 katlı bir sonsuzluk olarak temsil edilir, ancak � içeriyorsa o zaman 3 katlı bir sonsuzluk olarak temsil edilir.
Şimdi bir “çizgi fonksiyonu” düşünün:
��+��+�=0
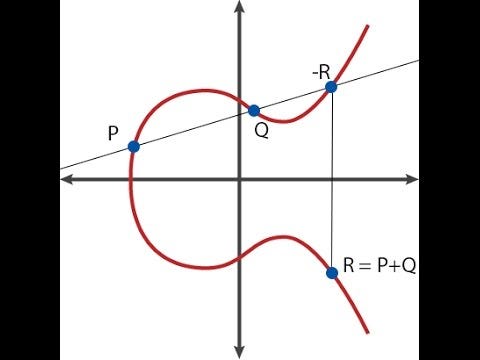
Burada �, � ve � doğrunun � ve � noktalarından geçmesini sağlayacak şekilde dikkatlice seçilir. Eliptik eğri toplamanın işleyişinden dolayı (üstteki diyagrama bakın), bu aynı zamanda onun -�−" içinden geçtiği anlamına da gelir. Ve hem � hem de �'ye bağlı olarak sonsuza kadar gider, dolayısıyla bölen [�]+[�]+[−�−�]−3⋅[�] olur.

Herhangi iki � ve � fonksiyonu için, �⋅�'nin böleni, �'nin böleni artı �'nin bölenine eşittir (matematik ders kitaplarında (�⋅�)=(�)+(�) göreceksiniz), yani örneğin eğer �(�,�)=��−� ise (�3)=3⋅[�]+3⋅[−�]−6⋅[�]; � ve −� belirli bir matematiksel anlamda �3'ün bu noktalarda "üç kat daha hızlı" 0'a yaklaşması gerçeğini açıklamak için "üçlü sayılır".
Bir fonksiyonun böleninden "köşeli parantezleri çıkarırsanız" noktaların toplamının �([�]+[�]+[−�−�]−3⋅[ olması gerektiğini belirten bir teorem olduğuna dikkat edin. �] açıkça uyar, �+�−�−�−3⋅�=�) ve bu özelliğe sahip herhangi bir bölen, bir fonksiyonun böleni olur.
Artık Tate eşleşmelerine bakmaya hazırız. Bölenleri aracılığıyla tanımlanan aşağıdaki işlevleri göz önünde bulundurun:
- (��)=�⋅[�]−�⋅[�], burada �, �1’in mertebesidir, yani. �⋅�=� herhangi bir � için
- (��)=�⋅[�]−�⋅[�]
- (�)=[�+�]−[�]−[�]+[�]
Şimdi ��⋅��⋅�� ürününe bakalım. Bölen:
�⋅[�]−�⋅[�]+�⋅[�]−�⋅[�]+�⋅[�+�]−�⋅[�]−�⋅[�]+�⋅[�]
Bu, aşağıdakileri düzgün bir şekilde basitleştirir:
�⋅[�+�]−�⋅[�]
Bu bölenin yukarıdaki �� ve �� böleniyle tamamen aynı formatta olduğuna dikkat edin. Dolayısıyla ��⋅��⋅��=��+� olur.
Şimdi “son üs alma” adımı adı verilen, yukarıdaki fonksiyonlarımızın sonucunu (��,��, vb.) alıp �=(�12−1)/� kuvvetine çıkardığımız bir prosedür uyguluyoruz, burada �12−1 (��)12’deki çarpımsal grubun mertebesidir (örn. herhangi �∈(��)12,�(�12−1)=1). Bu üssü herhangi bir sonuca uygularsanız, dikkat edin. zaten �'nin üssüne yükseltildiğinde, �12−1'in üssü elde edilir, dolayısıyla sonuç 1'e dönüşür. Dolayısıyla, son üstelleştirmeden sonra �� sadeleşir ve ���⋅���=( elde edilir. ��+�)�. Sizin için biraz çift doğrusallık var.
Şimdi, her iki argümanda da çift doğrusal olan bir fonksiyon yapmak istiyorsanız, daha spookie matematiğe girmeniz gerekir; burada bir değerin �� değerini doğrudan almak yerine, bir değerin �� değerini alırsınız. bölenve tam "Tate eşleşmesi" buradan geliyor. Daha fazla sonuç kanıtlamak için "doğrusal eşdeğerlik" ve "Weil karşılıklılığı" gibi kavramlarla uğraşmanız gerekir ve tavşan deliği buradan devam eder. Tüm bunlarla ilgili daha fazla okuma materyali bulabilirsiniz okuyun ve okuyun.
Optimum Ate eşleştirme adı verilen Tate eşleştirmesinin değiştirilmiş bir versiyonunun uygulanması için, buraya bakın. Kod uygular Miller'in algoritması��’yi hesaplamak için gereklidir.
Bunun gibi eşleştirmelerin mümkün olmasının karışık bir nimet olduğuna dikkat edin: bir yandan bu, eşleştirmelerle yapabileceğimiz tüm protokollerin mümkün olduğu anlamına gelir, ancak aynı zamanda eliptik eğrilerin hangileri olduğu konusunda daha dikkatli olmamız gerektiği anlamına da gelir. kullanırız.
Her eliptik eğrinin adı verilen bir değeri vardır. yerleştirme derecesi; esas itibariyle en küçük � öyle ki ��−1 �'nin bir katıdır (burada � alan için kullanılan asal sayıdır ve � eğri sırasıdır). Yukarıdaki alanlarda, ϵ=12 ve geleneksel ECC için kullanılan alanlarda (yani eşleştirmeleri umursamadığımız yerlerde), yerleştirme derecesi genellikle eşleşmelerin hesaplama açısından olanaksız olduğu noktaya kadar aşırı derecede büyüktür; ancak dikkatli olmazsak �=4 hatta 1 olan alanlar oluşturabiliriz.
Eğer �=1 ise, o zaman eliptik eğriler için "ayrık logaritma" sorunu (esasen, yalnızca �=�⋅� noktasını bilmek, bir eliptik eğri özel anahtarını "kırmak" için çözmeniz gereken sorun) kurtarılabilir) azaltılabilir �� üzerinde benzer bir matematik problemine dönüştürün, burada problem çok daha kolay hale gelir (buna MOV saldırısı); Gömme derecesi 12 veya daha yüksek olan eğrilerin kullanılması, bu azaltmanın ya kullanılamayacağını ya da eşleştirme sonuçları üzerinden ayrık log probleminin çözülmesinin, en azından özel bir anahtarın genel anahtardan "normal yolla" kurtarılması kadar zor olmasını sağlar (ör. hesaplama açısından mümkün değildir). Üzülmeyin; Bu sorun için tüm standart eğri parametreleri kapsamlı bir şekilde kontrol edilmiştir.
zk-SNARK'ların nasıl çalıştığına dair matematiksel bir açıklama çok yakında gelecek, bizi takip etmeye devam edin.
İnceleme ve düzeltmeler yapan Christian Reitwiessner, Ariel Gabizon (Zcash'tan) ve Alfred Menezes'e özellikle teşekkür ederiz.
- SEO Destekli İçerik ve Halkla İlişkiler Dağıtımı. Bugün Gücünüzü Artırın.
- PlatoData.Network Dikey Üretken Yapay Zeka. Kendine güç ver. Buradan Erişin.
- PlatoAiStream. Web3 Zekası. Bilgi Genişletildi. Buradan Erişin.
- PlatoESG. karbon, temiz teknoloji, Enerji, Çevre, Güneş, Atık Yönetimi. Buradan Erişin.
- PlatoSağlık. Biyoteknoloji ve Klinik Araştırmalar Zekası. Buradan Erişin.
- Blok Ofsetleri. Çevre Dengeleme Sahipliğini Modernleştirme. Buradan Erişin.
- Kaynak: Plato Veri Zekası.



