Giriş
Bu yazımızda ne olduğunu araştıracağız. hipotez testi, sıfır ve alternatif hipotezlerin formülasyonuna odaklanarak, hipotez testleri oluşturarak parametrik ve parametrik olmayan testlere derinlemesine dalacağız, bunların ilgili varsayımlarını ve Python'daki uygulamalarını tartışacağız. Ancak asıl odak noktamız Mann-Whitney U testi ve Kruskal-Wallis testi gibi parametrik olmayan testler olacaktır. Sonunda, hipotez testlerine ve bu kavramları kendi istatistiksel analizlerinize uygulayabileceğiniz pratik araçlara ilişkin kapsamlı bir anlayışa sahip olacaksınız.
Öğrenme hedefleri
- Sıfır ve alternatif hipotezlerin formülasyonu da dahil olmak üzere hipotez testinin ilkelerini anlayın.
- Hipotez Testinin Kurulması.
- Parametrik Test ve türlerinin anlaşılması.
- Parametrik Olmayan Testler, çeşitleri ve uygulamalarının anlaşılması.
- Parametrik ve Parametrik Olmayan Arasındaki Fark.
İçindekiler
Hipotez Testi Nedir?
Hipotez, bir kişi/kurum tarafından ortaya atılan iddiadır. İddia genellikle ortalama veya oran gibi popülasyon parametreleriyle ilgilidir ve iddiayı desteklemek için bir örnekten kanıt ararız.
Bazen anlamlılık testi olarak da adlandırılan hipotez testi, bir numunede ölçülen verileri kullanarak bir popülasyondaki bir parametre hakkındaki bir iddiayı veya hipotezi doğrulamak için kullanılan bir yöntemdir. Bu yöntemi kullanarak, nüfus parametresi hipotezi doğru olsaydı örnek bir istatistiğin seçilebileceği olasılığını belirleyerek çeşitli teorileri araştırırız.
Hipotez testi iki hipotezin formüle edilmesini içerir:
- Boş hipotez (H0)
- Alternatif hipotez (H1)
Sıfır hipotezi : Genellikle farkın olmadığı bir hipotezdir ve genellikle H0 ile gösterilir. RA Fisher'a göre boş hipotez, doğru olduğu varsayımı altında olası reddedilme açısından test edilen hipotezdir (Ref Fundamentals of Mathematicalstatistics).
Alternatif hipotez: Sıfır hipotezini tamamlayan herhangi bir hipoteze alternatif hipotez denir ve genellikle H1 ile gösterilir.
Hipotez testinin amacı, iki değişken (genellikle bir bağımsız ve bir bağımlı değişken, yani genellikle biri neden, diğeri sonuçtur) arasında istatistiksel olarak anlamlı bir ilişki kurmak için boş bir hipotezi ya reddetmek ya da korumaktır.
Hipotez Testinin Kurulması
- Hipotezi kelimelerle açıklayın veya bir iddiada bulunun.
- İddiaya dayanarak boş ve alternatif hipotezleri tanımlayın.
- Yukarıdaki iddiaya uygun hipotez testi türünü belirleyin.
- Sıfır hipotezinin geçerliliğini test etmek için kullanılacak test istatistiklerini belirleyin.
- Boş hipotezin reddedilmesi ve korunmasına ilişkin kriterleri belirleyin. Buna geleneksel olarak α (alfa) sembolüyle gösterilen anlamlılık değeri denir.
- Sıfır hipotezi doğru olduğunda test istatistik değerinin gözlemlenmesinin koşullu olasılığı olan p değerini hesaplayın. Basit bir ifadeyle p değeri, sıfır hipotezini destekleyen kanıttır.
Parametrik ve Parametrik Olmayan Test
Parametrik olmayan istatistiksel testler, verilerin örneklendiği popülasyon dağılımlarının parametreleri hakkındaki varsayımlara dayanmazken, parametrik istatistiksel testler bunu yapar.
Parametrik Testler
Çoğu istatistiksel test, temeli olarak bir dizi varsayım kullanılarak gerçekleştirilir. Analiz, belirli varsayımların ihlal edilmesi durumunda yanıltıcı veya tamamen yanlış sonuçlara yol açabilir.
Tipik olarak varsayımlar şunlardır:
- Normallik: Test edilecek parametrelerin örnekleme dağılımı normal (veya en azından simetrik) bir dağılım izler.
- Varyansların homojenliği: İki farklı popülasyondan gelen popülasyon ortalamalarını test etmediğimiz sürece, verilerin varyansı farklı gruplar arasında aynıdır.
Parametrik testlerden bazıları şunlardır:
- Z testi: Popülasyon standart sapması bilindiğinde popülasyon ortalaması, varyansı veya oranı için test yapın.
- Öğrencinin t testi: Popülasyon standart sapması bilinmediğinde popülasyon ortalaması, varyansı veya oranı için test yapın.
- Eşleştirilmiş t testi: İlgili iki grup veya koşulun ortalamalarını karşılaştırmak için kullanılır.
- Varyans Analizi (ANOVA): Üç veya daha fazla bağımsız gruptaki ortalamaları karşılaştırmak için kullanılır.
- Regresyon analizi: Bir veya daha fazla bağımsız değişken ile bağımlı değişken arasındaki ilişkiyi değerlendirmek için kullanılır.
- Kovaryans Analizi (ANCOVA): Analize ek değişkenler ekleyerek ANOVA'yı genişletir.
- Çok Değişkenli Varyans Analizi (MANOVA): Gruplar arasında birden fazla bağımlı değişkendeki farklılıkları değerlendirmek için ANOVA'yı genişletir.
Şimdi parametrik olmayan teste derinlemesine dalalım.
Parametrik olmayan test
Wolfowitz "parametrik olmayan" terimini ilk kez 1942'de kullandı. Parametrik olmayan istatistik fikrini anlamak için öncelikle az önce tartıştığımız parametrik istatistikle ilgili temel bir anlayışa sahip olmak gerekir. A parametrik test belirli bir dağılıma (genellikle normal) uyan bir örnek gerektirir. Ayrıca parametrik olmayan testler normallik gibi parametrik varsayımlardan bağımsızdır.
Parametrik olmayan testler (nüfusun dağılımı hakkında varsayımları olmadığından dağılımdan bağımsız testler olarak da bilinir). Parametrik olmayan testler, testlerin verilerin bir kaynaktan alındığı varsayımlarına dayanmadığını ima eder. olasılık dağılımı ortalama, orantı ve standart sapma gibi parametrelerle tanımlanır.
Parametrik olmayan testler şu durumlarda kullanılır:
- Test ortalama veya oran gibi nüfus parametreleriyle ilgili değildir.
- Yöntem, nüfus dağılımı hakkında varsayımlar gerektirmez (nüfusun normal bir dağılım izlemesi gibi).
Parametrik Olmayan Test Türleri
Şimdi Ki-Kare testi, Mann-Whitney testi, Wilcoxon İşaretli Sıra testi ve Kruskal-Wallis testlerini yapmanın konseptini ve prosedürünü tartışalım:
Ki-kare testi
İki niteliksel değişken arasındaki ilişkinin istatistiksel olarak anlamlı olup olmadığını belirlemek için Ki-Kare Testi adı verilen bir anlamlılık testinin yapılması gerekir.
İki ana Ki-Kare testi türü vardır:
Ki-Kare Uyum İyiliği
Bilinmeyen bir dağılıma sahip bir popülasyonun, bilinen bir dağılıma "uyup uymadığına" karar vermek için uyum iyiliği testini kullanın. Bu durumda tek bir nitel araştırma sorusu veya tek bir popülasyondan elde edilen bir deneyin tek bir sonucu olacaktır. Uyum İyiliği genellikle popülasyonun tekdüze olup olmadığını (tüm sonuçlar eşit sıklıkta meydana gelir), popülasyonun normal olup olmadığını veya popülasyonun bilinen bir dağılıma sahip başka bir popülasyonla aynı olup olmadığını görmek için kullanılır. Boş ve alternatif hipotezler şunlardır:
- H0: Popülasyon verilen dağılıma uyuyor.
- Ha: Popülasyon verilen dağılıma uymuyor.
Bunu bir örnekle anlayalım
| Gün | Pazartesi | Salı | Çarşamba | Perşembe | Cuma | Cumartesi | Pazar |
| Arıza Sayısı | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
Tablo, bir faktördeki arıza sayısını göstermektedir. Bu örnekte yalnızca tek bir değişken vardır ve gözlemlenen dağılımın (tabloda verilen) beklenen Dağılım'a uyup uymadığını belirlememiz gerekir.
Bunun için sıfır hipotezi ve alternatif hipotez şu şekilde formüle edilecektir:
- H0: Arızalar eşit olarak dağıtılır.
- Ha: Arızalar eşit şekilde dağılmamıştır.
Serbestlik derecesi de n-1 olacaktır (bu durumda n=7 yani df = 7-1=6)
Expected value will be= (14+22+16+18+12+19+11)/7=16
| Gün | Pazartesi | Salı | Çarşamba | Perşembe | Cuma | Cumartesi | Pazar |
| Arıza Sayısı (gözlenen) | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
| beklenen | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| (gözlenen-beklenen) | -2 | 6 | 0 | 2 | -4 | 3 | -5 |
| (gözlenen-beklenen)^2 | 4 | 36 | 0 | 4 | 16 | 9 | 25 |
Bu formülü kullanarak Ki-kareyi hesaplayın
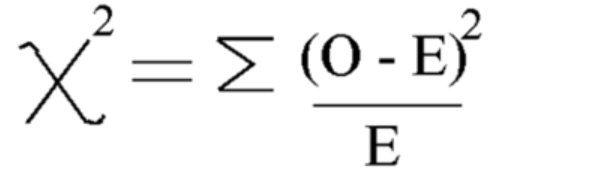
Ki-kare = 5.875
Ve serbestlik derecesi = n-1=7-1=6
Şimdi kritik değeri görelim ki kare dağılım tablosu %5 anlamlılık düzeyinde
Yani kritik değer 12.592
Hesaplanan Ki-Kare değeri kritik değerden küçük olduğundan sıfır hipotezini kabul ediyoruz ve kırılımların düzgün dağıldığı sonucuna varabiliyoruz.
Testin Ki-Kare Bağımsızlığı
İki değişkenin (faktörün) bağımsız mı yoksa bağımlı mı olduğuna, yani bu iki değişkenin aralarında anlamlı bir ilişki olup olmadığına karar vermek için bağımsızlık testini kullanın. Bu durumda iki niteliksel anket sorusu veya deneyi olacak ve bir olasılık tablosu oluşturulacaktır. Amaç, iki değişkenin ilgisiz mi (bağımsız) yoksa ilişkili mi (bağımlı) olduğunu görmektir. Boş ve alternatif hipotezler şunlardır:
- H0: İki değişken (faktör) bağımsızdır.
- Ha: İki değişken (faktör) bağımlıdır.
bir örnek alalım
Cinsiyet ve tercih edilen gömlek renginin bağımsız olup olmadığını araştırmak istediğimiz örnek. Bu, bir kişinin cinsiyetinin renk seçimini etkileyip etkilemediğini öğrenmek istediğimiz anlamına gelir. Bir anket yaptık ve verileri tablo halinde düzenledik.
Bu tabloda gözlemlenen değerler:
| Siyah | Beyaz | Kırmızı | Mavi | |
| Erkek | 48 | 12 | 33 | 57 |
| Kadın | 34 | 46 | 42 | 26 |
Şimdi ilk önce boş ve alternatif hipotezleri formüle edin
- H0: Cinsiyet ve tercih edilen gömlek rengi bağımsızdır
- Ha: Cinsiyet ve tercih edilen gömlek rengi bağımsız değildir
Ki-kare test istatistiklerini hesaplamak için beklenen değeri hesaplamamız gerekir. Böylece tüm satırları, sütunları ve genel toplamları ekleyin:
| Siyah | Beyaz | Kırmızı | Mavi | Toplam | |
| Erkek | 48 | 12 | 33 | 57 | 150 |
| Kadın | 34 | 46 | 42 | 26 | 148 |
| Toplam | 82 | 58 | 75 | 83 | 298 |
Bundan sonra, bu formülü = (satır toplamı * sütun toplamı)/genel toplam kullanarak her giriş için yukarıdaki tablodan beklenen değer tablosunu hesaplayabiliriz.
Beklenen değer tablosu:
| Siyah | Beyaz | Kırmızı | Mavi | |
| Erkek | 41.3 | 29.2 | 37.8 | 41.8 |
| Kadın | 40.7 | 28.8 | 37.2 | 41.2 |
Şimdi Ki-Kare Testi formülünü kullanarak Ki-kare değerini hesaplayın:
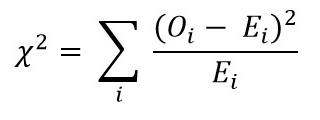
- Oi = Gözlemlenen Değer
- Ei = Beklenen Değer
Elde ettiğimiz değer: Χ2 = 34.9572
Serbestlik Derecesini Hesaplayın
DF=(satır sayısı-1)*(sütun sayısı-1)
Şimdi kritik değeri bulun ve ki-kare testiyle karşılaştırın istatistik değeri:
Bunu yapmak için serbestlik derecesine ve önem düzeyine (alfa) bakabilirsiniz. ki-kare dağılım tablosu
Alfa =0.050'de kritik değer= 7.815 elde edeceğiz
Ki-kare>kritik değer olduğundan
Bu nedenle sıfır hipotezini reddediyoruz ve cinsiyet ile tercih edilen gömlek renginin bağımsız olmadığı sonucuna varabiliyoruz.
Ki-Kare Uygulaması
Şimdi Python'da gerçek hayattan bazı örnekler kullanarak Ki-Kare uygulamasını görelim:
- H0: Cinsiyet ve tercih edilen gömlek rengi bağımsızdır
- Ha: Cinsiyet ve tercih edilen gömlek rengi bağımsız değildir
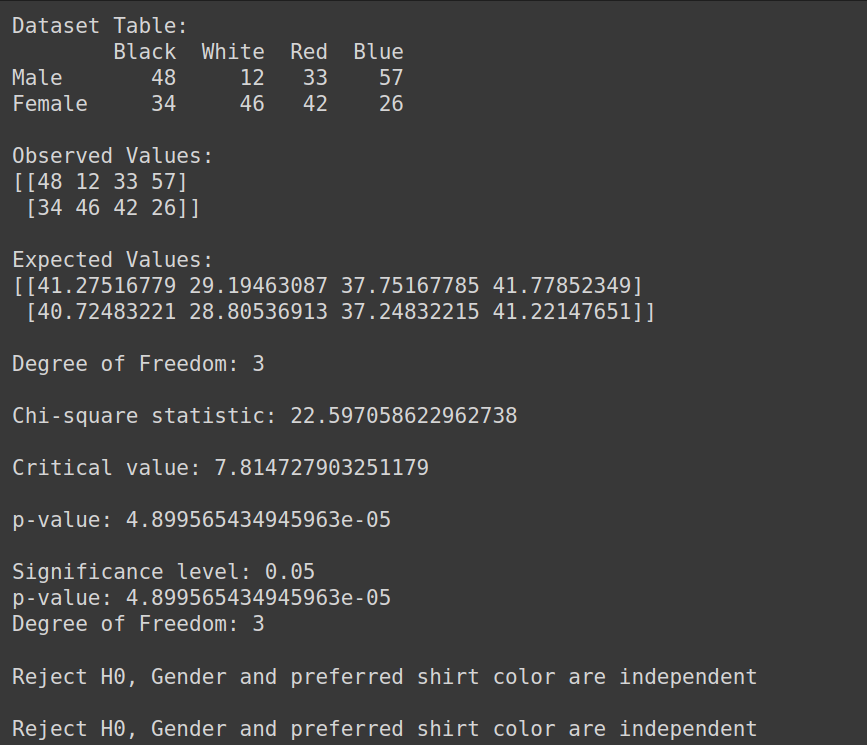
Veri Kümesi Oluşturma:
import pandas as pd
from scipy.stats import chi2_contingency
from scipy.stats import chi2
# Given dataset
df_dict = {
'Black': [48, 34],
'White': [12, 46],
'Red': [33, 42],
'Blue': [57, 26]
}
dataset_table = pd.DataFrame(df_dict, index=['Male', 'Female'])
print("Dataset Table:")
print(dataset_table)
print()
# Observed Values
Observed_Values = dataset_table.values
print("Observed Values:")
print(Observed_Values)
print()
# Perform chi-square test
val = chi2_contingency(dataset_table)
Expected_Values = val[3]
print("Expected Values:")
print(Expected_Values)
print()
# Degree of Freedom
no_of_rows = len(dataset_table.iloc[0:2, 0])
no_of_columns = 4
ddof = (no_of_rows - 1) * (no_of_columns - 1)
print("Degree of Freedom:", ddof)
print()
# Chi-square statistic
chi_square = sum([(o - e) ** 2. / e for o, e in zip(Observed_Values, Expected_Values)])
chi_square_statistic = chi_square[0] + chi_square[1]
print("Chi-square statistic:", chi_square_statistic)
print()
# Critical value
alpha = 0.05
critical_value = chi2.ppf(q=1-alpha, df=ddof)
print('Critical value:', critical_value)
print()
# p-value
p_value = 1 - chi2.cdf(x=chi_square_statistic, df=ddof)
print('p-value:', p_value)
print()
# Significance level
print('Significance level:', alpha)
print('p-value:', p_value)
print('Degree of Freedom:', ddof)
print()
# Hypothesis testing
if chi_square_statistic >= critical_value:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
print()
if p_value <= alpha:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
Çıktı:
Mann-Whitney U Testi
Mann-Whitney U testi, bağımsız örneklem t testinin parametrik olmayan alternatifi olarak hizmet eder. Aynı popülasyondan iki örnek ortalamayı karşılaştırarak eşit olup olmadıklarını belirler. Bu test genellikle sıralı veriler için veya t testinin varsayımları karşılanmadığında kullanılır.
Mann-Whitney U testi, her iki gruptaki tüm değerleri birlikte sıralar, ardından her grubun sıralarını toplar. Bu sıralamalara göre test istatistiği U'yu hesaplar. U istatistiği bir tablodaki kritik bir değerle karşılaştırılır veya bir yaklaşım kullanılarak hesaplanır. U istatistiği kritik değerden küçükse sıfır hipotezi reddedilir.
Bu, ortalamaları karşılaştıran ve normal dağılım varsayan t testi gibi parametrik testlerden farklıdır. Mann-Whitney U testi bunun yerine sıralamaları karşılaştırır ve normal dağılım varsayımını gerektirmez.
Mann-Whitney U testini anlamak zor olabilir çünkü sonuçlar grup ortalama farklılıklarından ziyade grup sıralama farklılıklarıyla sunulur.
Mann-Whitney Testi Formülü:
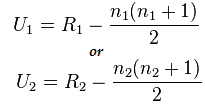
U= dk(U1,U2)
Burada,
- U= Mann-Whitney U Testi
- n1= örneklem büyüklüğü bir
- n2= örneklem büyüklüğü iki
- R1= Örneklem büyüklüğünün sıralaması bir
- R2= Örneklem büyüklüğü 2'nin sırası
O halde bunu kısa bir örnekle anlayalım:
Hasta sağlığını iyileştirmede iki farklı Tedavi yönteminin (Yöntem A ve Yöntem B) etkinliğini karşılaştırmak istediğimizi varsayalım. Aşağıdaki verilere sahibiz:
- Yöntem A: 3,4,2,6,2,5
- Yöntem B: 9,7,5,10,6,8
Burada verilerin normal dağılmadığını ve örneklem büyüklüklerinin küçük olduğunu görebiliriz.
Mann-Whitney U testinin uygulanması
Şimdi Mann-Whitney U testini yapalım:
Ama önce Boş ve Alternatif hipotezini formüle edelim
- H0: Her tedavinin Sıralaması arasında fark yoktur
- Ha: Her tedavinin Sıralaması arasında fark vardır
Tüm tedavileri birleştirin: 3,4,2,6,2,5,9,7,5,10,6,8
Sıralanmış veriler: 2,2,3,4,5,5,6,6,7,8,9,10
Sıralanan verilerin sıralaması: 1,2,3,4,5,6,7,8,9,10,11,12
- Verileri Ayrı Ayrı Sıralamak:
- Method A: 3(3),4(4),2(1.5),6(7.5),2(1.5),5(5.5)
- Method B: 9(11),7(9),5(5.5),10(12),6(1.5),8(10)
- Sıra toplamının hesaplanması):
- R1: 3+4+1.5+7.5+1.5+5.5=23
- R2: 11+9+5.5+12+1.5+10=55
Şimdi bu formülü kullanarak istatistik değerini hesaplayın:
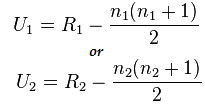
Burada n1=6 ve n2=6
U1=2 ve U2= 34 için hesaplama sonrası değer
U istatistiğinin hesaplanması:
Us= min(U1,U2)= min(2,34)= 2
Konum Mann-Whitney Masası kritik değeri bulabiliriz
Bu durumda Kritik Değer 5 olacaktır
Uc= 5 %5 anlamlılık düzeyinde Us'tan büyük olduğundan reddediyoruz. H0
Dolayısıyla her tedavinin Sıralaması arasında bir fark olduğu sonucuna varabiliriz.
Python ile uygulama
from scipy.stats import mannwhitneyu, norm
import numpy as np
TreatmentA = np.array([3,4,2,6,2,5])
TreatmentB = np.array([9,7,5,10,6,8])
# Perform Mann-Whitney U test
U_statistic, p_value = mannwhitneyu(TreatmentA, TreatmentB)
# Print the result
print(f'The U-statistic is {U_statistic:.2f} and the p-value is {p_value:.4f}')
if p_value < 0.05:
print("Reject Null Hypothesis: There is a significant difference between the Rank of each treatment.")
else:
print("Fail to Reject Null Hypothesis: Fail to Reject Null Hypothesis: There is no enough evidence to conclude that there is difference between the Rank of each treatment")Çıktı:

Kruskal –Wallis Testi
Kruskal –Wallis Testi çoklu gruplarla kullanılır. Varyansların normalliği ve eşitliği varsayımları ihlal edildiğinde, tek yönlü ANOVA testinin parametrik olmayan ve değerli bir alternatifidir. Kruskal –Wallis Testi ikiden fazla bağımsız grubun medyanlarını karşılaştırır.
Popülasyonlar için normallik koşulunu gerektirmeden, aynı dağılımlara sahip bir popülasyondan k bağımsız örnek (k>=3) çekildiğinde Boş Hipotezini test eder.
Varsayımlar:
Bağımsız olarak çizilmiş en az üç rastgele örnek olduğundan emin olun. Her numunenin en az 5 gözlemi vardır, n>=5
Üç grup öğrencinin kullandığı çalışma tekniğinin sınav puanlarını etkileyip etkilemediğini belirlemek istediğimiz bir örneği düşünün. Verileri analiz etmek ve gruplar arasında sınav puanları arasında istatistiksel olarak anlamlı farklılıklar olup olmadığını değerlendirmek için Kruskal-Wallis Testini kullanabiliriz.
Bunun için sıfır hipotezini şu şekilde formüle edin:
- H0: Üç grup öğrenci arasında sınav puanları açısından fark yoktur.
- Ha: Üç grup öğrenci arasında sınav puanları arasında fark vardır.
Wilcoxon İşaretli Sıra Testi
Wilcoxon İşaretli Sıralama Testi (Wilcoxon Eşleşen Çift Testi olarak da bilinir), bağımlı örnek t-testi veya eşleştirilmiş örnek t-testinin parametrik olmayan versiyonudur. İşaret testi, eşleştirilmiş örnek t testinin diğer parametrik olmayan alternatifidir. İlgilenilen değişkenler doğası gereği ikili olduğunda (Erkek ve Kadın, Evet ve Hayır gibi) kullanılır. Wilcoxon İşaretli Sıralama Testi aynı zamanda tek örnek t-testinin parametrik olmayan bir versiyonudur. Wilcoxon İşaretli Sıra Testi, grupların medyanlarını iki durum altında (eşleştirilmiş örnekler) veya grubun medyanını varsayılan medyanla (tek örnek) karşılaştırır.
Bunu bir örnekle anlayalım. Elimizde sigara içenlerin 8 haftalık bir programa katılmadan önceki ve sonraki günlük sigara tüketimlerine ilişkin verilerimiz olduğunu ve program öncesi ve sonrasında günlük sigara tüketiminde anlamlı bir fark olup olmadığını belirlemek istediğimizi varsayalım. bu testi kullan
Bunun için hipotez formülasyonu şu şekilde olacaktır:
- H0: Program öncesi ve sonrası günlük sigara tüketiminde fark yoktur.
- Ha: Program öncesi ve sonrası günlük sigara tüketiminde fark var
Normallik Testi
Şimdi Normallik testlerini tartışalım:
Shapiro Wilk testi
Shapiro-Wilk testi, belirli bir veri örneğinin normal dağılıma sahip bir popülasyondan gelip gelmediğini değerlendirir. Normalliği kontrol etmek için en sık kullanılan testlerden biridir. Test özellikle nispeten küçük numune boyutlarıyla uğraşırken kullanışlıdır.
Shapiro-Wilk testinde:
- Sıfır hipotezi : Örnek veriler normal dağılıma uyan bir popülasyondan gelir.
- Alternatif hipotez : Örnek veriler normal dağılıma uyan bir popülasyondan gelmiyor.
Shapiro-Wilk testi tarafından oluşturulan test istatistiği, normallik varsayımı altında gözlemlenen veriler ile beklenen veriler arasındaki tutarsızlığı ölçer. Test istatistiğiyle ilişkili p değeri seçilen anlamlılık seviyesinden (örneğin, 0.05) düşükse, verilerin normal şekilde dağılmadığını belirten boş hipotezi reddederiz. Eğer p değeri anlamlılık seviyesinden büyükse, boş hipotezi reddedemeyiz, bu da verilerin normal bir dağılım izleyebileceğini öne sürer.
Öncelikle bu testler için bir veri seti oluşturalım, istediğiniz herhangi bir veri setini kullanabilirsiniz:
import pandas as pd
# Create the dictionary with the provided data
data = {
'population': [6.1101, 5.5277, 8.5186, 7.0032, 5.8598],
'profit': [17.5920, 9.1302, 13.6620, 11.8540, 6.8233]
}
# Create the DataFrame
df = pd.DataFrame(data)
response_var=df['profit']
Here, a sample for running Shapiro -Wilk test on python:
from scipy.stats import shapiro
stat, p_val = shapiro(response_var)
print(f'Shapiro-Wilk Test: Statistic={stat} p-value={p_val}')
if p_val > alpha:
print('Data looks normal (fail to reject H0)')
else:
print('Data looks normal (fail to reject H0)')Çıktı:

Bu test nispeten küçük numune boyutları (n=< 50-2000) için en uygun olanıdır çünkü daha büyük numune boyutlarıyla daha az güvenilir hale gelir.
Anderson-Darling
Belirli bir veri örneğinin normal dağılım gibi belirli bir dağılımdan gelip gelmediğini değerlendirir. Shapiro-Wilk testine benzer ancak özellikle daha küçük numune boyutları için daha duyarlıdır.
Dağılım parametrelerinin bilinmediği durumlar için normal dağılım da dahil olmak üzere birçok dağılıma uygundur.
İşte, Uygulamak için Python kodu:
from scipy.stats import anderson
response_var = data['profit']
alpha = 0.05
# Anderson-Darling Test
result = anderson(response_var)
print(f'Anderson statistics: {result.statistic:.3f}')
if result.statistic > result.critical_values[-1]:
p_value = 0.0 # The p-value is essentially 0 if the statistic exceeds the largest critical value
else:
p_value = result.significance_level[result.statistic < result.critical_values][-1]
print("P-value:", p_value)
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")Çıktı:

Jarque-Bera Testi
Jarque-Bera testi, belirli bir veri örneğinin normal dağılım gösteren bir popülasyondan gelip gelmediğini değerlendirir. Verilerin çarpıklığına ve basıklığına dayanır.
Jarque-Bera Testinin Python'da örnek verilerle uygulanması:
from scipy.stats import jarque_bera
# Performing Jarque-Bera test
test_statistic, p_value = jarque_bera(response_var)
print("Jarque-Bera Test Statistic:", test_statistic)
print("P-value:", p_value)
# Interpreting results
alpha = 0.05
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")Çıktı:

| Kategoriler | Parametrik İstatistik Teknikleri | Parametrik Olmayan İstatistikteknikleri |
| ilişki | Pearson Moment Çarpımı Korelasyon Katsayısı (r) | Spearman Sıra Katsayısı Korelasyonu (Rho), Kendall's Tau |
| İki grup, bağımsız önlemler | Bağımsız t testi | Mann-Whitney U testi |
| İkiden fazla grup, bağımsız önlemler | Tek yönlü ANOVA | Kruskal-Wallis tek yönlü ANOVA |
| İki grup, tekrarlanan ölçümler | eşleştirilmiş t testi | Wilcoxon eşleştirilmiş çift imzalı sıralama testi |
| İkiden fazla grup, tekrarlanan ölçümler | Tek yönlü, tekrarlanan ölçümler ANOVA | Friedman'ın iki yönlü Varyans Analizi |
Sonuç
Hipotez testi Örnek verileri kullanarak popülasyon parametreleri hakkındaki iddiaları değerlendirmek için gereklidir. Parametrik testler belirli varsayımlara dayanır ve aralık veya oran verileri için uygundur; parametrik olmayan testler ise daha esnektir ve katı dağılım varsayımları olmadan nominal veya sıralı verilere uygulanabilir. Shapiro-Wilk ve Anderson-Darling gibi testler normalliği değerlendirirken, Ki-kare ve Jarque-Bera uyumun iyiliğini değerlendirir. Parametrik ve parametrik olmayan testler arasındaki farkları anlamak, uygun istatistiksel yaklaşımın seçilmesi açısından çok önemlidir. Genel olarak hipotez testi, veriye dayalı kararlar almak ve ampirik kanıtlardan güvenilir sonuçlar çıkarmak için sistematik bir çerçeve sağlar.
Gelişmiş istatistiksel analizde uzmanlaşmaya hazır mısınız? BlackBelt Veri Analizi kursumuza bugün kaydolun! Hipotez testleri, parametrik ve parametrik olmayan testler, Python uygulaması ve daha pek çok konuda uzmanlık kazanın. İstatistiksel becerilerinizi geliştirin ve veriye dayalı karar vermede uzmanlaşın. Şimdi Katıl!
Sık Sorulan Sorular
A. Parametrik testler popülasyon dağılımı ve normallik ve varyansın homojenliği gibi parametreler hakkında varsayımlarda bulunurken, parametrik olmayan testler bu varsayımlara dayanmaz. Parametrik testler, varsayımlar karşılandığında daha fazla güce sahipken, parametrik olmayan testler daha sağlamdır ve verilerin çarpık olduğu veya normal dağılmadığı durumlar da dahil olmak üzere daha geniş bir yelpazedeki durumlarda uygulanabilir.
C. İki kategorik değişken arasında anlamlı bir ilişki olup olmadığını belirlemek için ki-kare testi kullanılır. Genellikle kategorik verileri analiz eder ve beklenmedik durum tablolarındaki değişkenlerin bağımsızlığı hakkındaki hipotezleri test eder.
A. Mann-Whitney U testi, bağımlı değişken sıralı olduğunda veya normal dağılmadığında iki bağımsız grubu karşılaştırır. İki grubun medyanları arasında anlamlı bir fark olup olmadığını değerlendirir.
A. Shapiro-Wilk testi, bir örneğin normal dağılıma sahip bir popülasyondan gelip gelmediğini değerlendirir. Verilerin normal dağılıma uyduğu yönündeki boş hipotezi test eder. P değeri seçilen anlamlılık seviyesinden (örneğin, 0.05) düşükse, boş hipotezi reddederek verilerin normal dağılmadığı sonucuna varırız.
- SEO Destekli İçerik ve Halkla İlişkiler Dağıtımı. Bugün Gücünüzü Artırın.
- PlatoData.Network Dikey Üretken Yapay Zeka. Kendine güç ver. Buradan Erişin.
- PlatoAiStream. Web3 Zekası. Bilgi Genişletildi. Buradan Erişin.
- PlatoESG. karbon, temiz teknoloji, Enerji, Çevre, Güneş, Atık Yönetimi. Buradan Erişin.
- PlatoSağlık. Biyoteknoloji ve Klinik Araştırmalar Zekası. Buradan Erişin.
- Kaynak: https://www.analyticsvidhya.com/blog/2024/04/a-comprehensive-guide-on-non-parametric-tests/



