Vitalik Buterin przez Blog Vitalika Buterina

To jest lustrzane odbicie postu pod adresem https://medium.com/@VitalikButerin/odkrywanie-eliptycznych-parowania-c73c1864e627

Ostrzeżenie o uruchomieniu: matematyka.

Jednym z kluczowych prymitywów kryptograficznych stojących za różnymi konstrukcjami, w tym deterministycznymi sygnaturami progowymi, zk-SNARK i innymi prostszymi formami dowodów o wiedzy zerowej, jest parowanie krzywych eliptycznych. Pary krzywych eliptycznych (lub „mapy dwuliniowe”) to najnowszy dodatek do 30-letniej historii wykorzystania krzywych eliptycznych w zastosowaniach kryptograficznych, w tym w szyfrowaniu i podpisach cyfrowych; parowania wprowadzają formę „szyfrowanego mnożenia”, znacznie rozszerzając możliwości protokołów opartych na krzywych eliptycznych. Celem tego artykułu będzie szczegółowe omówienie par krzywych eliptycznych i wyjaśnienie ogólnego zarysu ich działania.

Nie oczekuje się, że zrozumiesz wszystko za pierwszym razem, ani nawet za dziesiątym razem; ta sprawa jest naprawdę trudna. Miejmy jednak nadzieję, że ten artykuł da wam choć trochę pojęcia o tym, co dzieje się pod maską.

Krzywe eliptyczne same w sobie są tematem nietrywialnym do zrozumienia i w tym artykule ogólnie zakładamy, że wiesz, jak one działają; jeśli nie, polecam ten artykuł tutaj jako elementarz: https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/. Krótko mówiąc, kryptografia krzywych eliptycznych obejmuje obiekty matematyczne zwane „punktami” (są to dosłowne dwuwymiarowe punkty o współrzędnych (�,�)), ze specjalnymi wzorami ich dodawania i odejmowania (tj. obliczania współrzędnych �= �+�), możesz także pomnożyć punkt przez liczbę całkowitą (tj. �⋅�=�+�+…+�, choć istnieje znacznie szybszy sposób obliczenia, jeśli � jest duże).

Oto jak graficznie wygląda dodawanie punktów.

Istnieje specjalny punkt zwany „punktem w nieskończoności” (�), który jest odpowiednikiem zera w arytmetyce punktowej; zawsze jest tak, że �+�=�. Ponadto krzywa ma „zamówienie„; istnieje liczba � taka, że ​​�⋅�=� dla dowolnego � (i oczywiście �⋅(�+1)=�,�⋅(7⋅�+5)=�⋅5 i tak dalej). Istnieje również powszechnie przyjęty „punkt generatora” �, który w pewnym sensie reprezentuje liczbę 1. Teoretycznie każdy punkt na krzywej (z wyjątkiem �) może być �; liczy się tylko to, że � jest ustandaryzowane.

Parowanie idzie o krok dalej, ponieważ pozwala sprawdzić pewne rodzaje bardziej skomplikowanych równań na punktach krzywej eliptycznej — na przykład, jeśli �=�⋅�,�=�⋅� i �=�⋅�, można sprawdzić, czy lub nie �⋅�=�, mając tylko �,� i � jako dane wejściowe. Może się to wydawać, że podstawowe gwarancje bezpieczeństwa krzywych eliptycznych są łamane, ponieważ informacja o � wycieka od samej znajomości P, ale okazuje się, że wyciek jest wysoce ograniczony — w szczególności decyzyjny problem Diffiego Hellmana jest łatwe, ale obliczeniowy problem Diffiego Hellmana (znając � i � w powyższym przykładzie, computing �=�⋅�⋅�) i problem logarytmu dyskretnego (odzyskiwanie � z �) pozostają obliczeniowo niewykonalne (przynajmniej, jeśli były wcześniej).

Trzeci sposób spojrzenia na działanie parowania, być może najbardziej pouczający w większości przypadków użycia, o których mówimy, polega na tym, że postrzegasz punkty krzywej eliptycznej jako liczby zaszyfrowane jednokierunkowo (tj. ���� ���(�)=�⋅�=�), to podczas gdy tradycyjna matematyka dotycząca krzywych eliptycznych pozwala sprawdzić liniowy ograniczenia dotyczące liczb (np. jeśli �=�⋅�,�=�⋅� i �=�⋅�, sprawdzanie 5⋅�+7⋅�=11⋅� jest naprawdę sprawdzenie, że 5⋅�+7⋅�=11⋅�), pary pozwalają sprawdzić kwadratowy ograniczenia (np. sprawdzanie �(�,�)⋅�(�,�⋅5)=1 to naprawdę sprawdzając, że �⋅�+5=0). A przejście do funkcji kwadratowej wystarczy, abyśmy mogli pracować z deterministycznymi sygnaturami progowymi, kwadratowymi programami arytmetycznymi i wszystkimi innymi dobrymi rzeczami.

A teraz, co to za zabawny operator �(�,�), który przedstawiliśmy powyżej? To jest parowanie. Matematycy czasami nazywają to również a mapa dwuliniowa; słowo „bilinearny” zasadniczo oznacza tutaj, że spełnia ograniczenia:

�(�,�+�)=�(�,�)⋅�(�,�)

�(�+�,�)=�(�,�)⋅�(�,�)

Zauważ, że + i ⋅ mogą być dowolnymi operatorami; kiedy tworzysz fantazyjne nowe rodzaje obiektów matematycznych, algebra abstrakcyjna nie dba o to, jak są + i ⋅ zdefiniowane, o ile są spójne w zwykły sposób, np. �+�=�+�,(�⋅�)⋅�=�⋅(�⋅�) i (�⋅�)+(�⋅�)=(�+�)⋅�.

Gdyby �, �, � i � były proste z naszej, to wykonanie prostego parowania jest łatwe: możemy wykonać �(�,�)=2��. Następnie możemy zobaczyć:

�(3,4+5)=23⋅9=227

�(3,4)⋅�(3,5)=23⋅4⋅23⋅5=212⋅215=227

To jest dwuliniowe!

Jednak takie proste pary nie nadają się do kryptografii, ponieważ obiekty, na których działają, są prostymi liczbami całkowitymi i są zbyt łatwe do analizy; liczby całkowite ułatwiają dzielenie, obliczanie logarytmów i wykonywanie różnych innych obliczeń; proste liczby całkowite nie mają pojęcia „klucza publicznego” ani „funkcji jednokierunkowej”. Dodatkowo, dzięki opisanemu powyżej parowaniu, możesz cofnąć się – znając � i znając �(�,�), możesz po prostu obliczyć dzielenie i logarytm, aby wyznaczyć �. Zależy nam na obiektach matematycznych jak najbliżej „czarnych skrzynek”, w których można dodawać, odejmować, mnożyć i dzielić, ale nie rób nic więcej. W tym miejscu pojawiają się krzywe eliptyczne i pary krzywych eliptycznych.

Okazuje się, że możliwe jest utworzenie dwuliniowego odwzorowania punktów krzywej eliptycznej — to znaczy wynalezienie funkcji �(�,�), w której dane wejściowe � i � są punktami krzywej eliptycznej, a wynikiem jest tzw. (��)12 elementu (przynajmniej w konkretnym przypadku, który tutaj omówimy; szczegóły różnią się w zależności od szczegółów krzywej, więcej o tym później), ale matematyka stojąca za tym jest dość złożona.

Najpierw omówmy pola pierwsze i pola rozszerzone. Ładna eliptyczna krzywa na obrazku wcześniej w tym poście wygląda w ten sposób tylko wtedy, gdy założymy, że równanie krzywej jest zdefiniowane przy użyciu zwykłych liczb rzeczywistych. Jeśli jednak faktycznie używamy w kryptografii zwykłych liczb rzeczywistych, wówczas można użyć logarytmów, aby „cofać się” i wszystko się psuje; dodatkowo ilość miejsca potrzebnego do faktycznego przechowywania i przedstawiania liczb może dowolnie rosnąć. Dlatego zamiast tego używamy liczb w a główne pole.

Pole pierwsze składa się ze zbioru liczb 0,1,2…�−1, gdzie � jest liczbą pierwszą, a różne operacje są zdefiniowane w następujący sposób:

�+�:(�+�) % �

�⋅�:(�⋅�) % �

�−�:(�−�) % �

�/�:(�⋅��−2) % �

Zasadniczo całą matematykę wykonuje się modulo � (patrz tutaj wprowadzenie do matematyki modułowej). Podział jest przypadkiem szczególnym; zwykle 32 nie jest liczbą całkowitą i tutaj chcemy mieć do czynienia tylko z liczbami całkowitymi, więc zamiast tego staramy się znaleźć liczbę � taką, że �⋅2=3, gdzie ⋅ oczywiście odnosi się do mnożenia modułowego zgodnie z definicją powyżej. Dzięki Małe twierdzenie Fermata, pokazana powyżej sztuczka z potęgowaniem spełnia swoje zadanie, ale można to zrobić także szybciej, korzystając z metody Rozszerzony algorytm euklidesowy. Załóżmy, że �=7; oto kilka przykładów:

2+3=5 % 7=5

4+6=10 % 7=3

2−5=−3 % 7=4

6⋅3=18 % 7=4

3/2=(3⋅25) % 7=5

5⋅2=10 % 7=3

Jeśli pobawisz się tego rodzaju matematyką, zauważysz, że jest ona całkowicie spójna i spełnia wszystkie zwykłe zasady. Ostatnie dwa przykłady powyżej pokazują, jak (�/�)⋅�=�; możesz także zobaczyć, że (�+�)+�=�+(�+�),(�+�)⋅�=�⋅�+�⋅� i wszystkie inne tożsamości algebraiczne ze szkoły średniej, które znasz i lubisz, trwają aby również było prawdą. W rzeczywistości na krzywych eliptycznych punkty i równania są zwykle obliczane w polach pierwszych.

Porozmawiajmy teraz pola rozszerzeń. Prawdopodobnie widziałeś już pole rozszerzenia; najczęstszym przykładem, jaki można spotkać w podręcznikach do matematyki, jest pole liczb zespolonych, gdzie pole liczb rzeczywistych jest „rozszerzane” o dodatkowy element −1=�. Zasadniczo pola rozszerzeń działają poprzez wzięcie istniejącego pola, następnie „wynalezienie” nowego elementu i zdefiniowanie relacji między tym elementem a istniejącymi elementami (w tym przypadku �2+1=0), upewniając się, że to równanie nie jest prawdziwe dla dowolnej liczby znajdującej się w pierwotnym polu i patrząc na zbiór wszystkich kombinacji liniowych elementów pierwotnego pola i nowego elementu, który właśnie utworzyłeś.

Możemy także dokonać rozszerzeń pól pierwszych; na przykład możemy rozszerzyć pole pierwsze mod7, które opisaliśmy powyżej, o �, a następnie możemy wykonać:

(2+3�)+(4+2�)=6+5�

(5+2�)+3=1+2�

(6+2�)⋅2=5+4�

4�⋅(2+�)=3+�

Ten ostatni wynik może być nieco trudny do zrozumienia; Stało się tak, że najpierw rozkładamy iloczyn na 4�⋅2+4�⋅�, co daje 8�−4, a następnie, ponieważ pracujemy w matematyce mod7, wychodzi �+3. Aby podzielić, robimy:

�/�:(�⋅�(�2−2)) % �

Zauważ, że wykładnikiem małego twierdzenia Fermata jest teraz �2 zamiast �, chociaż po raz kolejny, jeśli chcemy być bardziej wydajni, możemy zamiast tego rozszerzyć Rozszerzony Algorytm Euklidesa, aby wykonał to zadanie. Zauważ, że ��2−1=1 dla dowolnego � w tym polu, zatem �2−1 nazywamy „rządem grupy multiplikatywnej w polu”.

W przypadku liczb rzeczywistych tzw Podstawowe twierdzenie algebry zapewnia, że ​​rozszerzenie kwadratowe, które nazywamy liczbami zespolonymi, jest „kompletne” — nie można go dalej rozszerzać, ponieważ dla dowolnej zależności matematycznej (przynajmniej dowolnej zależności matematycznej określonej wzorem algebraicznym), jaką można wymyślić pomiędzy jakimś nowym elementem � i istniejących liczb zespolonych, można znaleźć co najmniej jedną liczbę zespoloną, która już spełnia tę zależność. Jednakże w przypadku pól pierwszych nie mamy tego problemu, więc możemy pójść dalej i dokonać rozszerzeń sześciennych (gdzie matematyczna relacja między jakimś nowym elementem � a istniejącymi elementami pola jest równaniem sześciennym, więc 1,� i �2 to wszystkie liniowo niezależne od siebie), rozszerzenia wyższego rzędu, rozszerzenia rozszerzeń itp. I to właśnie na tego rodzaju doładowanych modułowych liczbach zespolonych budowane są pary krzywych eliptycznych.

Dla tych, którzy chcą zobaczyć dokładną matematykę związaną z zapisywaniem wszystkich tych operacji w kodzie, zaimplementowano tutaj pola pierwsze i rozszerzenia pól: https://github.com/ethereum/py_pairing/blob/master/py_ecc/bn128/bn128_field_elements.py

Przejdźmy teraz do parowania krzywych eliptycznych. Parowanie na krzywej eliptycznej (a raczej specyficzna forma parowania, którą tutaj omówimy; istnieją również inne typy par, choć ich logika jest dość podobna) to mapa �2×�1 →��, gdzie:

• �1 jest krzywą eliptyczną, na której punkty spełniają równanie postaci �2=�3+� i gdzie obie współrzędne są elementami �� (tzn. są to liczby proste, z wyjątkiem tego, że arytmetyka jest wykonywana modulo pewnej liczby pierwszej)
• �2 to krzywa eliptyczna, na której punkty spełniają to samo równanie co �1, z wyjątkiem sytuacji, gdy współrzędne są elementami (��)12 (tzn. są to doładowane liczby zespolone, o których mówiliśmy powyżej; definiujemy nową „liczbę magiczną” ” �, który jest zdefiniowany przez wielomian 12 stopnia, np. �12−18⋅�6+82=0)
• �� to typ obiektu, do którego trafia wynik krzywej eliptycznej. Na krzywych, które oglądamy, �� wynosi (��)12 (ta sama doładowana liczba zespolona, ​​jak użyta w �2)

Główną właściwością, jaką musi spełniać, jest dwuliniowość, co w tym kontekście oznacza, że:

• �(�,�+�)=�(�,�)⋅�(�,�)
• �(�+�,�)=�(�,�)⋅�(�,�)

Istnieją jeszcze dwa inne ważne kryteria:

• Wydajna obliczalność (np. możemy dokonać łatwego parowania, po prostu biorąc logarytmy dyskretne wszystkich punktów i mnożąc je przez siebie, ale jest to tak samo trudne obliczeniowo, jak przede wszystkim złamanie kryptografii krzywej eliptycznej, więc to się nie liczy)
• Niedegeneracja (oczywiście, możesz po prostu zdefiniować �(�,�)=1, ale nie jest to szczególnie przydatne połączenie)

Więc jak to robimy?

Matematyczne wyjaśnienie działania funkcji parowania jest dość trudne i wymaga sporo zaawansowanej algebry, wykraczającej nawet poza to, co widzieliśmy do tej pory, ale przedstawię zarys. Przede wszystkim należy zdefiniować pojęcie a rozdzielacz, w zasadzie alternatywny sposób przedstawiania funkcji na punktach krzywej eliptycznej. Dzielnik funkcji zasadniczo zlicza zera i nieskończoności funkcji. Aby zobaczyć, co to oznacza, przeanalizujmy kilka przykładów. Ustalmy pewien punkt �=(��,��) i rozważmy następującą funkcję:

�(�,�)=�−��

Dzielnik to [�]+[−�]−2⋅[�] (nawiasy kwadratowe służą do przedstawienia faktu, że mówimy o obecność punktu � w zbiorze zer i nieskończoności funkcji, a nie sam punkt P; [�]+[�] jest nie to samo co [�+�]). Uzasadnienie jest następujące:

• Funkcja jest równa zero w �, ponieważ � is ��, więc �−��=0
• Funkcja jest równa zeru w −�, ponieważ −� i � mają tę samą współrzędną �
• Funkcja zmierza do nieskończoności, tak jak � zmierza do nieskończoności, więc mówimy, że funkcja jest równa nieskończoności w �. Istnieje techniczny powód, dla którego tę nieskończoność należy policzyć dwukrotnie, więc � zostaje dodane z „wielokrotnością” wynoszącą -2 (ujemną, ponieważ jest to nieskończoność, a nie zero, dwa z powodu podwójnego liczenia).

Powód techniczny jest z grubsza taki: ponieważ równanie krzywej to �3=�2+�,� dąży do nieskończoności „1.5 razy szybciej” niż �, aby �2 dotrzymało �3; stąd, jeśli funkcja liniowa zawiera tylko �, to jest reprezentowana jako nieskończoność krotności 2, ale jeśli zawiera �, to jest reprezentowana jako nieskończoność krotności 3.

Rozważmy teraz „funkcję liniową”:

��+��+�=0

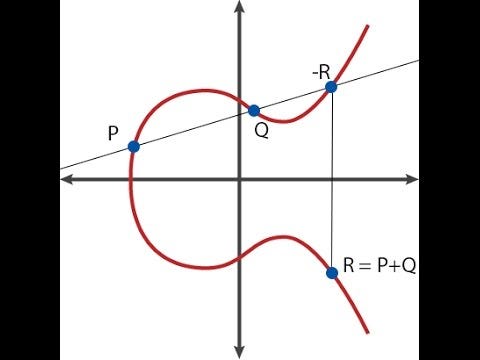
Gdzie �, � i � są starannie dobrane tak, aby linia przechodziła przez punkty � i �. Ze względu na sposób działania dodawania krzywej eliptycznej (patrz diagram na górze) oznacza to również, że przechodzi ona przez −�−�. I to zmierza do nieskończoności, zależnie od � i �, więc dzielnik staje się [�]+[�]+[−�−�]−3⋅[�].

Wiemy, że każda „funkcja wymierna” (tj. funkcja zdefiniowana jedynie przy użyciu skończonej liczby operacji +, −, ⋅ i / na współrzędnych punktu) jednoznacznie odpowiada pewnemu dzielnikowi, aż do pomnożenia przez stałą (tj. jeśli dwie funkcje � i � mają ten sam dzielnik, to �=�⋅� dla pewnej stałej �).

Dla dowolnych dwóch funkcji � i � dzielnik �⋅� jest równy dzielnikowi � plus dzielnik � (w podręcznikach matematyki zobaczysz (�⋅�)=(�)+(�)), więc na przykład jeśli �(�,�)=��−�, to (�3)=3⋅[�]+3⋅[−�]−6⋅[�]; � i −� są „liczone potrójnie”, aby uwzględnić fakt, że �3 zbliża się do 0 w tych punktach „trzy razy szybciej” w pewnym sensie matematycznym.

Zauważ, że istnieje twierdzenie, które stwierdza, że ​​jeśli „usuniesz nawiasy kwadratowe” z dzielnika funkcji, suma punktów musi wynosić �([�]+[�]+[−�−�]−3⋅[ �] wyraźnie pasuje, ponieważ �+�−�−�−3⋅�=�), a każdy dzielnik posiadający tę własność jest dzielnikiem funkcji.

Teraz jesteśmy gotowi, aby przyjrzeć się parom Tate. Rozważmy następujące funkcje zdefiniowane poprzez ich dzielniki:

• (��)=�⋅[�]−�⋅[�], gdzie � jest rządem �1, tj. �⋅�=� dla dowolnego �
• (��)=�⋅[�]−�⋅[�]
• (�)=[�+�]−[�]−[�]+[�]

Przyjrzyjmy się teraz produktowi ��⋅��⋅��. Dzielnik to:

�⋅[�]−�⋅[�]+�⋅[�]−�⋅[�]+�⋅[�+�]−�⋅[�]−�⋅[�]+�⋅[�]

Co upraszcza starannie do:

�⋅[�+�]−�⋅[�]

Zauważ, że ten dzielnik ma dokładnie taki sam format jak dzielnik �� i �� powyżej. Zatem ��⋅��⋅��=��+�.

Teraz wprowadzamy procedurę zwaną krokiem „końcowego potęgowania”, w której wynik naszych funkcji powyżej (��,�� itd.) podnosimy do potęgi �=(�12−1)/�, gdzie �12−1 jest rzędem grupy multiplikatywnej w (��)12 (tj. dla każdy �∈(��)12,�(�12−1)=1). Zauważ, że jeśli zastosujesz to potęgowanie do dowolnego wyniku, który ma już podniesione do potęgi �, otrzymujemy potęgowanie do potęgi �12−1, więc wynik zamienia się w 1. Zatem po końcowym potęgowaniu �� znosi się i otrzymujemy ���⋅���=( ��+�)�. Jest w tobie pewna dwuliniowość.

Teraz, jeśli chcesz utworzyć funkcję dwuliniową w obu argumentach, musisz przejść do bardziej przerażającej matematyki, gdzie zamiast bezpośrednio przyjmować �� wartości, bierzesz �� z rozdzielaczi stąd właśnie pochodzi pełne „parowanie Tate”. Aby udowodnić więcej wyników, musisz uporać się z pojęciami takimi jak „równoważność liniowa” i „wzajemność Weila”, a od tego zaczyna się królicza nora. Możesz znaleźć więcej materiałów do przeczytania na ten temat tutaj i tutaj.

W celu wdrożenia zmodyfikowanej wersji parowania Tate, zwanej optymalnym parowaniem Ate, Spójrz tutaj. Kod implementuje Algorytm Millera, co jest potrzebne do faktycznego obliczenia ��.

Należy zauważyć, że fakt, że takie pary są możliwe, jest błogosławieństwem mieszanym: z jednej strony oznacza to, że wszystkie protokoły, które możemy wykonać w przypadku parowania, stają się możliwe, ale oznacza również, że musimy bardziej uważać na to, jakie krzywe eliptyczne Używamy.

Każda krzywa eliptyczna ma wartość zwaną an stopień osadzania; zasadniczo najmniejsze � takie, że ��−1 jest wielokrotnością � (gdzie � jest liczbą pierwszą używaną dla pola, a � jest porządkiem krzywej). W powyższych polach, �=12, oraz w polach używanych w tradycyjnym ECC (tj. gdzie nie dbamy o pary), stopień osadzania jest często niezwykle duży, do tego stopnia, że ​​obliczenia parowania są obliczeniowe; jeśli jednak nie będziemy ostrożni, możemy wygenerować pola, w których �=4 lub nawet 1.

Jeśli �=1, to problem „logarytmu dyskretnego” dla krzywych eliptycznych (zasadniczo odzyskiwanie � znając tylko punkt �=�⋅�, problem, który trzeba rozwiązać, aby „złamać” klucz prywatny krzywej eliptycznej) można zmniejszyć w podobny problem matematyczny nad ��, gdzie problem staje się znacznie łatwiejszy (jest to tzw Atak MOV); użycie krzywych o stopniu osadzania 12 lub wyższym zapewnia, że ​​ta redukcja jest albo niedostępna, albo rozwiązanie problemu dziennika dyskretnego na wynikach parowania jest co najmniej tak samo trudne, jak odzyskanie klucza prywatnego z klucza publicznego „w normalny sposób” (tj. niewykonalne obliczeniowo). Nie martw się; wszystkie parametry krzywej standardowej zostały dokładnie sprawdzone pod kątem tego problemu.

Czekajcie na matematyczne wyjaśnienie działania zk-SNARK, które już wkrótce się pojawi.

Specjalne podziękowania dla Christiana Reitwiessnera, Ariela Gabizona (z Zcash) i Alfreda Menezesa za recenzję i wprowadzenie poprawek.

• Dystrybucja treści i PR oparta na SEO. Uzyskaj wzmocnienie już dziś.
• PlatoData.Network Pionowe generatywne AI. Wzmocnij się. Dostęp tutaj.
• PlatoAiStream. Inteligencja Web3. Wiedza wzmocniona. Dostęp tutaj.
• PlatonESG. Węgiel Czysta technologia, Energia, Środowisko, Słoneczny, Gospodarowanie odpadami. Dostęp tutaj.
• Platon Zdrowie. Inteligencja w zakresie biotechnologii i badań klinicznych. Dostęp tutaj.
• Przesunięcia bloków. Modernizacja własności offsetu środowiskowego. Dostęp tutaj.
• Źródło: Inteligencja danych Platona.