Elliptiske kurver er blant de mer forlokkende objektene i moderne matematikk. De virker ikke kompliserte, men de danner en motorvei mellom matematikken som mange lærer på videregående og forsker på matematikk på sitt mest dype. De var sentrale i Andrew Wiles' feirede bevis på Fermats siste teorem på 1990-tallet. De er nøkkelverktøy i moderne kryptografi. Og i 2000 kåret Clay Mathematics Institute a gjetninger om statistikken av elliptiske kurver en av syv "Millennium Prize Problemer", som hver har en premie på 1 million dollar for sin løsning. Den formodningen, først våget av Bryan Birch og Peter Swinnerton-Dyer på 1960-tallet, har fortsatt ikke blitt bevist.

Å forstå elliptiske kurver er en høy innsats som har vært sentral i matematikk. Så i 2022, da et transatlantisk samarbeid brukte statistiske teknikker og kunstig intelligens for å oppdage helt uventede mønstre i elliptiske kurver, var det et velkomment, om enn uventet, bidrag. "Det var bare et spørsmål om tid før maskinlæring havnet foran dørstokken vår med noe interessant," sa Peter Sarnak, en matematiker ved Institute for Advanced Study og Princeton University. I utgangspunktet var det ingen som kunne forklare hvorfor de nyoppdagede mønstrene eksisterer. Siden den gang, i en serie av nyere artikler, har matematikere begynt å låse opp årsakene bak mønstrene, kalt "murringer" for deres likhet med flytende formene til flokkende stær, og har begynt å bevise at de ikke bare må forekomme i det spesielle. eksempler undersøkt i 2022, men i elliptiske kurver mer generelt.

Viktigheten av å være elliptisk

For å forstå hva disse mønstrene er, må vi legge et lite grunnlag om hva elliptiske kurver er og hvordan matematikere kategoriserer dem.

En elliptisk kurve relaterer kvadratet til en variabel, vanligvis skrevet som y, til tredje potens av en annen, vanligvis skrevet som x: y² = x³ + Ax + B, for noen tallpar A og B, Så lenge A og B oppfylle noen enkle betingelser. Denne ligningen definerer en kurve som kan tegnes grafisk på planet, som vist nedenfor. (Til tross for likheten i navnene, er en ellipse ikke en elliptisk kurve.)

Selv om de ser enkle ut, viser elliptiske kurver seg å være utrolig kraftige verktøy for tallteoretikere - matematikere som ser etter mønstre i heltallene. I stedet for å la variablene x og y rekkevidde over alle tall, liker matematikere å begrense dem til forskjellige tallsystemer, som de kaller å definere en kurve "over" et gitt tallsystem. Elliptiske kurver begrenset til de rasjonelle tallene - tall som kan skrives som brøker - er spesielt nyttige. "Elliptiske kurver over reelle eller komplekse tall er ganske kjedelige," sa Sarnak. "Det er bare de rasjonelle tallene som er dype."

Her er en måte som er sann. Hvis du tegner en rett linje mellom to rasjonelle punkter på en elliptisk kurve, vil stedet der den linjen skjærer kurven igjen også være rasjonell. Du kan bruke dette faktum til å definere "addisjon" i en elliptisk kurve, som vist nedenfor.

Tegn en linje mellom P og Q. Den linjen vil skjære kurven ved et tredje punkt, R. (Matematikere har et spesielt triks for å håndtere tilfellet der linjen ikke skjærer kurven ved å legge til et "punkt ved uendelig.") Refleksjonen av R tvers over x-aksen er summen din P + Q. Sammen med denne addisjonsoperasjonen danner alle løsningene til kurven et matematisk objekt kalt en gruppe.

Matematikere bruker dette til å definere "rangen" til en kurve. De rangering av en kurve forholder seg til antall rasjonelle løsninger den har. Rank 0-kurver har et begrenset antall løsninger. Kurver med høyere rangering har uendelig antall løsninger hvis forhold til hverandre ved bruk av addisjonsoperasjonen er beskrevet av rangeringen.

Rangeringer er ikke godt forstått; matematikere har ikke alltid en måte å beregne dem på og vet ikke hvor store de kan bli. (Den største eksakte rangeringen kjent for en spesifikk kurve er 20.) Lignende kurver kan ha helt forskjellige rangeringer.

Elliptiske kurver har også mye å gjøre med primtall, som kun er delbare med 1 og seg selv. Spesielt ser matematikere på kurver over endelige felt - systemer av syklisk aritmetikk som er definert for hvert primtall. Et begrenset felt er som en klokke med antall timer lik primtall: Hvis du fortsetter å telle oppover, begynner tallene på nytt. I det endelige feltet for 7, for eksempel, er 5 pluss 2 lik null, og 5 pluss 3 er lik 1.

En elliptisk kurve har en tilhørende tallsekvens, kalt a_p, som er relatert til antall løsninger det er til kurven i det endelige feltet definert av primtall p. En mindre a_p betyr flere løsninger; en større a_p betyr færre løsninger. Selv om rangeringen er vanskelig å beregne, er sekvensen a_p er mye enklere.

På grunnlag av tallrike beregninger gjort på en av de aller første datamaskinene, antok Birch og Swinnerton-Dyer et forhold mellom rangeringen til en elliptisk kurve og sekvensen. a_p. Alle som kan bevise at de hadde rett, vil vinne en million dollar og matematisk udødelighet.

Et overraskelsesmønster dukker opp

Etter starten av pandemien, Yang-Hui He, en forsker ved London Institute for Mathematical Sciences, bestemte seg for å ta på seg noen nye utfordringer. Han hadde vært hovedfag i fysikk på college, og hadde tatt doktorgraden fra Massachusetts Institute of Technology i matematisk fysikk. Men han ble stadig mer interessert i tallteori, og gitt de økende evnene til kunstig intelligens, tenkte han at han ville prøve seg på å bruke AI som et verktøy for å finne uventede mønstre i tall. (Det hadde han allerede vært ved hjelp av maskinlæring å klassifisere Calabi-Yau manifolder, matematiske strukturer som er mye brukt i strengteori.)

I august 2020, etter hvert som pandemien ble dypere, var University of Nottingham vert for ham for en nettprat. Han var pessimistisk om fremgangen sin, og om muligheten for å bruke maskinlæring for å avdekke ny matematikk. "Hans fortelling var at tallteori var vanskelig fordi du ikke kunne maskinlære ting i tallteori," sa --Thomas Oliver, en matematiker ved University of Westminster som var blant publikum. Som han husker, "Jeg kunne ikke finne noe fordi jeg ikke var en ekspert. Jeg brukte ikke engang de riktige tingene for å se på dette.»

Oliver og Kyu-Hwan Lee, en matematiker ved University of Connecticut, begynte å jobbe med He. "Vi bestemte oss for å gjøre dette bare for å lære hva maskinlæring var, i stedet for å studere matematikk seriøst," sa Oliver. "Men vi fant raskt ut at du kunne maskinlære mange ting."

Oliver og Lee foreslo at han skulle bruke teknikkene sine for å undersøke L-funksjoner, uendelige serier nært knyttet til elliptiske kurver gjennom sekvensen a_p. De kunne bruke en online database med elliptiske kurver og deres relaterte L-funksjoner kalt LMFDB å trene maskinlæringsklassifikatorene sine. På det tidspunktet hadde databasen litt over 3 millioner elliptiske kurver over rasjonalene. I oktober 2020 hadde de et papir som brukte informasjon hentet fra L-funksjoner for å forutsi en bestemt egenskap ved elliptiske kurver. I november delte de et annet papir som brukte maskinlæring for å klassifisere andre objekter i tallteori. I desember klarte de det forutsi rekken av elliptiske kurver med høy nøyaktighet.

Men de var ikke sikre på hvorfor maskinlæringsalgoritmene deres fungerte så bra. Lee spurte sin bachelorstudent Alexey Pozdnyakov for å se om han kunne finne ut hva som foregikk. Som det skjer, sorterer LMFDB elliptiske kurver i henhold til en mengde kalt lederen, som oppsummerer informasjon om primtal som en kurve ikke klarer å oppføre seg godt for. Så Pozdnyakov prøvde å se på et stort antall kurver med lignende ledere samtidig - si alle kurvene med ledere mellom 7,500 og 10,000.

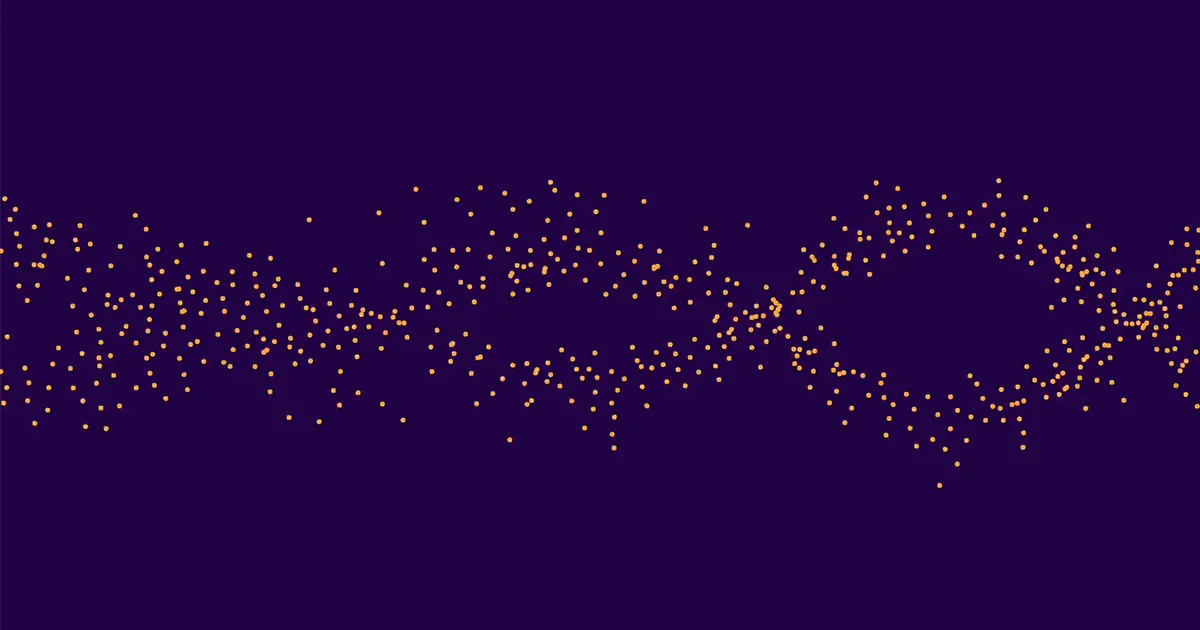
Dette utgjorde ca 10,000 0 kurver totalt. Omtrent halvparten av disse hadde rangering 1, og halvparten rangering XNUMX. (Høyere rangeringer er ekstremt sjeldne.) Han tok deretter gjennomsnittet av verdiene for a_p for alle rang 0-kurvene, separat gjennomsnittlig a_p for alle rang 1-kurvene, og plottet resultatene. De to settene med prikker dannet to distinkte, lett merkbare bølger. Det var grunnen til at maskinlæringsklassifikatorene hadde vært i stand til å fastslå rekken av bestemte kurver på riktig måte.

"Først følte jeg meg bare glad for at jeg hadde fullført oppgaven," sa Pozdnyakov. "Men Kyu-Hwan innså umiddelbart at dette mønsteret var overraskende, og det var da det ble virkelig spennende."

Lee og Oliver ble begeistret. "Alexey viste oss bildet, og jeg sa at det ser ut som det som fugler gjør," sa Oliver. "Og så slo Kyu-Hwan opp det og sa at det kalles en murring, og så sa Yang at vi skulle ringe avisen"Murmurering av elliptiske kurver. '”

De lastet opp papiret sitt i april 2022 og videresendte det til en håndfull andre matematikere, og ventet nervøst å bli fortalt at deres såkalte "oppdagelse" var velkjent. Oliver sa at forholdet var så synlig at det burde vært lagt merke til for lenge siden.

Nesten umiddelbart vakte fortrykket interesse, spesielt fra Andrew Sutherland, en forsker ved MIT som er en av de administrerende redaktørene for LMFDB. Sutherland innså at 3 millioner elliptiske kurver ikke var nok for hans formål. Han ønsket å se på mye større lederområder for å se hvor robuste murringene var. Han hentet data fra et annet enormt depot med rundt 150 millioner elliptiske kurver. Fortsatt misfornøyd hentet han data fra et annet depot med 300 millioner kurver.

"Men selv de var ikke nok, så jeg beregnet faktisk et nytt datasett med over en milliard elliptiske kurver, og det var det jeg brukte til å beregne de virkelig høyoppløselige bildene," sa Sutherland. Murringene viste seg om han i gjennomsnitt var over 15,000 XNUMX elliptiske kurver om gangen eller en million om gangen. Formen forble den samme selv når han så på kurvene over større og større primtall, et fenomen som kalles skalainvarians. Sutherland innså også at murringer ikke er unike for elliptiske kurver, men også vises mer generelt L-funksjoner. Han skrev et brev som oppsummerer funnene hans og sendte den til Sarnak og Michael Rubinstein ved University of Waterloo.

"Hvis det er en kjent forklaring på det, forventer jeg at du vil vite det," skrev Sutherland.

Det gjorde de ikke.

Forklarer mønsteret

Lee, He og Oliver organiserte en workshop om murringer i august 2023 ved Brown University's Institute for Computational and Experimental Research in Mathematics (ICERM). Sarnak og Rubinstein kom, det samme gjorde Sarnaks elev Nina Zubrilina.

Zubrilina presenterte sin forskning på murringmønstre i modulære former, spesielle komplekse funksjoner som i likhet med elliptiske kurver har assosiert L-funksjoner. I modulære former med store ledere konvergerer murringene til en skarpt definert kurve, i stedet for å danne et merkbart, men spredt mønster. I et papir postet 11. oktober 2023 beviste Zubrilina at denne typen murring følger en eksplisitt formel hun oppdaget.

«Ninas store prestasjon er at hun har gitt en formel for dette; Jeg kaller det Zubrilina murmurering tetthetsformel,» sa Sarnak. "Ved å bruke svært sofistikert matematikk har hun bevist en eksakt formel som passer perfekt til dataene."

Formelen hennes er komplisert, men Sarnak hyller den som en viktig ny type funksjon, sammenlignbar med Airy-funksjonene som definerer løsninger på differensialligninger som brukes i en rekke kontekster i fysikk, alt fra optikk til kvantemekanikk.

Selv om Zubrilinas formel var den første, har andre fulgt etter. "Hver uke nå, er det et nytt papir ute," sa Sarnak, "hovedsakelig ved å bruke Zubrilinas verktøy, som forklarer andre aspekter ved murring."

Jonathan Bober, Andrew Booker og Min lee fra University of Bristol, sammen med David Lowry-Duda av ICERM, beviste eksistensen av en annen type murring i modulære former i en annen oktoberavis. Og Kyu-Hwan Lee, Oliver og Pozdnyakov bevist eksistensen av murringer i objekter kalt Dirichlet-karakterer som er nært beslektet med L-funksjoner.

Sutherland var imponert over den betydelige dosen flaks som hadde ført til oppdagelsen av murringer. Hvis de elliptiske kurvedataene ikke hadde blitt bestilt av konduktøren, ville murringene ha forsvunnet. "De var heldige som tok data fra LMFDB, som kom forhåndssortert i henhold til konduktøren," sa han. "Det er det som relaterer en elliptisk kurve til den tilsvarende modulære formen, men det er slett ikke åpenbart. … To kurver hvis ligninger ser veldig like ut, kan ha svært forskjellige ledere.» For eksempel bemerket Sutherland det y² = x³ - 11x + 6 har leder 17, men snu minustegnet til et plusstegn, y² = x³ + 11x + 6 har konduktør 100,736.

Selv da ble murringene bare funnet på grunn av Pozdnyakovs uerfarenhet. "Jeg tror ikke vi ville ha funnet det uten ham," sa Oliver, "fordi ekspertene tradisjonelt normaliserer a_p å ha absolutt verdi 1. Men han normaliserte dem ikke ... så svingningene var veldig store og synlige.»

De statistiske mønstrene som AI-algoritmer bruker for å sortere elliptiske kurver etter rangering, eksisterer i et parameterrom med hundrevis av dimensjoner - for mange til at folk kan sortere i tankene deres, enn si visualisere, bemerket Oliver. Men selv om maskinlæring fant de skjulte svingningene, "forsto vi først senere at de var murringene."

Redaktørens merknad: Andrew Sutherland, Kyu-Hwan Lee og L-functions and modular forms database (LMFDB) har alle mottatt finansiering fra Simons Foundation, som også finansierer denne redaksjonelt uavhengige publikasjonen. Simons Foundations finansieringsbeslutninger har ingen innflytelse på vår dekning. Mer informasjon er tilgjengelig her..