Vitalik Buterin tramite il Blog di Vitalik Buterin

Questo è uno specchio del post su https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627

Avviso di attivazione: matematica.

Una delle primitive crittografiche chiave dietro varie costruzioni, tra cui firme di soglia deterministiche, zk-SNARK e altre forme più semplici di prove a conoscenza zero è l'accoppiamento di curve ellittiche. Gli accoppiamenti di curve ellittiche (o “mappe bilineari”) sono una recente aggiunta a una storia lunga 30 anni di utilizzo di curve ellittiche per applicazioni crittografiche tra cui crittografia e firme digitali; gli accoppiamenti introducono una forma di “moltiplicazione crittografata”, espandendo notevolmente ciò che possono fare i protocolli basati su curve ellittiche. Lo scopo di questo articolo sarà quello di approfondire in dettaglio gli accoppiamenti di curve ellittiche e spiegare uno schema generale di come funzionano.

Non ci si aspetta che tu capisca tutto qui la prima volta che lo leggi, e nemmeno la decima volta; questa roba è davvero difficile. Ma spero che questo articolo ti dia almeno un'idea di cosa sta succedendo sotto il cofano.

Le curve ellittiche stesse sono un argomento non banale da comprendere e questo articolo generalmente presuppone che tu sappia come funzionano; in caso contrario, ti consiglio questo articolo qui come introduzione: https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/. In breve, la crittografia a curva ellittica coinvolge oggetti matematici chiamati “punti” (si tratta di punti bidimensionali letterali con coordinate (�,�), con formule speciali per aggiungerli e sottrarli (ovvero per calcolare le coordinate di �= �+�) e puoi anche moltiplicare un punto per un numero intero (es. �⋅�=�+�+…+�, anche se esiste un modo molto più veloce per calcolarlo se � è grande).

Ecco come appare graficamente l'addizione di punti.

Esiste un punto speciale chiamato “punto all'infinito” (�), l'equivalente dello zero nell'aritmetica puntuale; è sempre vero che �+�=�. Inoltre, una curva ha un “minimo“; esiste un numero � tale che �⋅�=� per qualsiasi � (e ovviamente, �⋅(�+1)=�,�⋅(7⋅�+5)=�⋅5, e così via). Esiste anche un “punto generatore” comunemente concordato �, che in un certo senso rappresenta il numero 1. Teoricamente, qualsiasi punto su una curva (tranne �) può essere �; tutto ciò che conta è che � sia standardizzato.

Gli accoppiamenti fanno un ulteriore passo avanti in quanto consentono di verificare alcuni tipi di equazioni più complicate sui punti della curva ellittica: ad esempio, se �=�⋅�,�=�⋅� e �=�⋅�, è possibile verificare se o non �⋅�=�, avendo solo �,� e � come input. Potrebbe sembrare che le garanzie di sicurezza fondamentali delle curve ellittiche vengano infrante, poiché le informazioni su � trapelano solo conoscendo P, ma si scopre che la perdita è altamente contenuta - in particolare, la problema decisionale di Diffie Hellman è facile, ma il problema computazionale di Diffie Hellman (conoscendo � e � nell'esempio sopra, informatica �=�⋅�⋅�) e il problema del logaritmo discreto (recuperando � da �) rimangono computazionalmente irrealizzabili (almeno, se lo erano prima).

Un terzo modo per vedere cosa fanno gli accoppiamenti, e forse il più illuminante per la maggior parte dei casi d'uso di cui ci occupiamo, è che se si visualizzano i punti della curva ellittica come numeri crittografati unidirezionali (ovvero, ���� ���(�)=�⋅�=�), mentre la matematica tradizionale della curva ellittica ti consente di verificare lineare vincoli sui numeri (es. se �=�⋅�,�=�⋅� e �=�⋅�, controllare 5⋅�+7⋅�=11⋅� è veramente controllando che 5⋅�+7⋅�=11⋅�), gli accoppiamenti ti permettono di controllare quadratico vincoli (es. controllare �(�,�)⋅�(�,�⋅5)=1 è veramente verificando che �⋅�+5=0). E arrivare al quadratico è sufficiente per permetterci di lavorare con firme di soglia deterministiche, programmi di aritmetica quadratica e tutte quelle altre cose buone.

Ora, cos'è questo buffo operatore �(�,�) che abbiamo introdotto sopra? Questo è l'abbinamento. I matematici a volte lo chiamano anche a mappa bilineare; la parola “bilineare” qui significa sostanzialmente che soddisfa i vincoli:

�(�,�+�)=�(�,�)⋅�(�,�)

�(�+�,�)=�(�,�)⋅�(�,�)

Nota che + e ⋅ possono essere operatori arbitrari; quando crei nuovi fantasiosi tipi di oggetti matematici, all'algebra astratta non interessa come sono + e ⋅ definito, purché siano coerenti nei modi consueti, ad es. �+�=�+�,(�⋅�)⋅�=�⋅(�⋅�) e (�⋅�)+(�⋅�)=(�+�)⋅�.

Se �, �, � e � fossero semplici numeri, allora fare un semplice abbinamento è facile: possiamo fare �(�,�)=2��. Quindi, possiamo vedere:

�(3,4+5)=23⋅9=227

�(3,4)⋅�(3,5)=23⋅4⋅23⋅5=212⋅215=227

È bilineare!

Tuttavia, accoppiamenti così semplici non sono adatti alla crittografia perché gli oggetti su cui lavorano sono semplici numeri interi e sono troppo facili da analizzare; i numeri interi facilitano la divisione, il calcolo dei logaritmi e l'esecuzione di vari altri calcoli; gli interi semplici non hanno il concetto di “chiave pubblica” o di “funzione unidirezionale”. Inoltre, con l'abbinamento sopra descritto puoi tornare indietro: conoscendo � e conoscendo �(�,�), puoi semplicemente calcolare una divisione e un logaritmo per determinare �. Vogliamo oggetti matematici che si avvicinino il più possibile alle “scatole nere”, dove è possibile aggiungere, sottrarre, moltiplicare e dividere, ma non fare nient'altro. È qui che entrano in gioco le curve ellittiche e gli accoppiamenti di curve ellittiche.

Si scopre che è possibile creare una mappa bilineare su punti di curva ellittica, ovvero ottenere una funzione �(�,�) in cui gli input � e � sono punti di curva ellittica e dove l'output è ciò che viene chiamato (��)12 elemento (almeno nel caso specifico che tratteremo qui; le specifiche differiscono a seconda dei dettagli della curva, ne parleremo più avanti), ma i calcoli dietro a ciò sono piuttosto complessi.

Per prima cosa, esaminiamo i campi primi e quelli di estensione. La curva piuttosto ellittica nell'immagine all'inizio di questo post appare così solo se si presuppone che l'equazione della curva sia definita utilizzando numeri reali regolari. Tuttavia, se in realtà usiamo numeri reali regolari in crittografia, allora puoi usare i logaritmi per “andare indietro” e tutto si rompe; inoltre, la quantità di spazio necessaria per memorizzare e rappresentare effettivamente i numeri può crescere arbitrariamente. Quindi usiamo invece i numeri in a campo primo.

Un campo primo è costituito dall’insieme dei numeri 0,1,2…�−1, dove � è primo, e le varie operazioni sono definite come segue:

�+�:(�+�) % �

�⋅�:(�⋅�) % �

�−�:(�−�) % �

�/�:(�⋅��−2) % �

Fondamentalmente, tutti i calcoli vengono fatti modulo � (vedi qui per un'introduzione alla matematica modulare). La divisione è un caso speciale; normalmente, 32 non è un numero intero, e qui vogliamo trattare solo numeri interi, quindi proviamo invece a trovare il numero � tale che �⋅2=3, dove ⋅ ovviamente si riferisce alla moltiplicazione modulare come definita sopra. Grazie a Il piccolo teorema di Fermat, il trucco dell'elevamento a potenza mostrato sopra fa il lavoro, ma esiste anche un modo più veloce per farlo, usando il metodo Algoritmo euclideo esteso. Supponiamo che �=7; ecco alcuni esempi:

2+3=5 % 7=5

4+6=10 % 7=3

2−5=−3 % 7=4

6⋅3=18 % 7=4

3/2=(3⋅25) % 7=5

5⋅2=10 % 7=3

Se giochi con questo tipo di matematica, noterai che è perfettamente coerente e soddisfa tutte le solite regole. Gli ultimi due esempi sopra mostrano come (�/�)⋅�=�; puoi anche vedere che (�+�)+�=�+(�+�),(�+�)⋅�=�⋅�+�⋅�, e tutte le altre identità algebriche del liceo che conosci e ami continuano essere vero anch'esso. Nelle curve ellittiche, in realtà, i punti e le equazioni vengono solitamente calcolati in campi primi.

Ora parliamo campi di estensione. Probabilmente hai già visto un campo di estensione prima; l’esempio più comune che si incontra nei libri di matematica è il campo dei numeri complessi, dove il campo dei numeri reali viene “esteso” con l’elemento aggiuntivo −1=�. Fondamentalmente, i campi di estensione funzionano prendendo un campo esistente, quindi “inventando” un nuovo elemento e definendo la relazione tra quell’elemento e gli elementi esistenti (in questo caso, �2+1=0), assicurandosi che questa equazione non sia vera per qualsiasi numero presente nel campo originale e osservando l'insieme di tutte le combinazioni lineari di elementi del campo originale e del nuovo elemento che hai appena creato.

Possiamo anche fare estensioni di campi primi; ad esempio possiamo estendere il campo primo mod7 che abbiamo descritto sopra con �, e poi possiamo fare:

(2+3�)+(4+2�)=6+5�

(5+2�)+3=1+2�

(6+2�)⋅2=5+4�

4�⋅(2+�)=3+�

Quest'ultimo risultato potrebbe essere un po' difficile da capire; quello che è successo è che prima abbiamo scomposto il prodotto in 4�⋅2+4�⋅�, che dà 8�−4, e poi poiché stiamo lavorando con la matematica mod7 che diventa �+3. Per dividere facciamo:

�/�:(�⋅�(�2−2)) % �

Si noti che l'esponente del piccolo teorema di Fermat ora è �2 invece di �, anche se ancora una volta, se vogliamo essere più efficienti, possiamo anche estendere l'Algoritmo Euclideo Esteso per svolgere il lavoro. Si noti che ��2−1=1 per qualsiasi � in questo campo, quindi chiamiamo �2−1 “l’ordine del gruppo moltiplicativo nel campo”.

Con i numeri reali, il Teorema fondamentale dell'algebra assicura che l'estensione quadratica che chiamiamo numeri complessi sia "completa" - non puoi estenderla ulteriormente, perché per qualsiasi relazione matematica (almeno, qualsiasi relazione matematica definita da una formula algebrica) che puoi trovare tra qualche nuovo elemento � e i numeri complessi esistenti, è possibile trovare almeno un numero complesso che già soddisfi quella relazione. Con i campi primi, tuttavia, non abbiamo questo problema, quindi possiamo andare oltre e creare estensioni cubiche (dove la relazione matematica tra qualche nuovo elemento - e gli elementi del campo esistenti è un'equazione cubica, quindi 1, - e 2 sono tutti linearmente indipendenti l'uno dall'altro), estensioni di ordine superiore, estensioni di estensioni, ecc. Ed è su questi tipi di numeri complessi modulari sovralimentati che sono costruiti gli accoppiamenti di curve ellittiche.

Per coloro che sono interessati a vedere la matematica esatta coinvolta nell'esecuzione di tutte queste operazioni scritte nel codice, i campi prime e le estensioni dei campi sono implementati qui: https://github.com/ethereum/py_pairing/blob/master/py_ecc/bn128/bn128_field_elements.py

Passiamo ora agli accoppiamenti di curve ellittiche. Un accoppiamento di curve ellittiche (o meglio, la forma specifica di accoppiamento che esploreremo qui; esistono anche altri tipi di accoppiamenti, sebbene la loro logica sia abbastanza simile) è una mappa �2×�1→��, dove:

• �1 è una curva ellittica, dove i punti soddisfano un'equazione della forma �2=�3+�, e dove entrambe le coordinate sono elementi di �� (cioè sono numeri semplici, tranne che l'aritmetica è tutta fatta modulo qualche numero primo)
• �2 è una curva ellittica, dove i punti soddisfano la stessa equazione di �1, tranne dove le coordinate sono elementi di (��)12 (cioè sono i numeri complessi sovralimentati di cui abbiamo parlato sopra; definiamo un nuovo “numero magico ” �, che è definito da un polinomio di 12° grado come �12−18⋅�6+82=0)
• �� è il tipo di oggetto in cui va il risultato della curva ellittica. Nelle curve che osserviamo, �� è (��)12 (lo stesso numero complesso sovralimentato utilizzato in �2)

La proprietà principale che deve soddisfare è la bilinearità, che in questo contesto significa che:

• �(�,�+�)=�(�,�)⋅�(�,�)
• �(�+�,�)=�(�,�)⋅�(�,�)

Ci sono altri due criteri importanti:

• Calcolabilità efficiente (ad esempio, possiamo creare un abbinamento semplice semplicemente prendendo i logaritmi discreti di tutti i punti e moltiplicandoli insieme, ma questo è computazionalmente difficile quanto rompere la crittografia della curva ellittica in primo luogo, quindi non conta)
• Non degenerazione (certo, potresti semplicemente definire �(�,�)=1, ma non è un abbinamento particolarmente utile)

Come possiamo farlo?

I calcoli alla base del funzionamento delle funzioni di accoppiamento sono piuttosto complicati e richiedono un po' di algebra avanzata che va anche oltre ciò che abbiamo visto finora, ma fornirò uno schema. Innanzitutto occorre definire il concetto di a divisore, fondamentalmente un modo alternativo di rappresentare funzioni su punti di curve ellittiche. Un divisore di una funzione conta sostanzialmente gli zeri e gli infiniti della funzione. Per vedere cosa significa, facciamo alcuni esempi. Fissiamo un punto �=(��,��), e consideriamo la seguente funzione:

�(�,�)=�−��

Il divisore è [�]+[−�]−2⋅[�] (le parentesi quadre servono a rappresentare il fatto a cui ci riferiamo la presenza del punto � nell'insieme degli zeri e degli infiniti della funzione, non il punto P stesso; [�]+[�] è non la stessa cosa di [�+�]). Il ragionamento è il seguente:

• La funzione è uguale a zero in �, poiché � is ��, quindi �−��=0
• La funzione è uguale a zero in −�, poiché −� e � condividono la stessa coordinata �
• La funzione va all'infinito come � va all'infinito, quindi diciamo che la funzione è uguale all'infinito in �. C'è una ragione tecnica per cui questo infinito deve essere contato due volte, quindi � viene aggiunto con una “molteplicità” di −2 (negativa perché è un infinito e non uno zero, due a causa di questo doppio conteggio).

La ragione tecnica è più o meno questa: poiché l’equazione della curva è �3=�2+�,� va all’infinito “1.5 volte più velocemente” di � affinché �2 possa tenere il passo con �3; quindi, se una funzione lineare include solo � allora è rappresentata come un'infinità di molteplicità 2, ma se include � allora è rappresentata come un'infinità di molteplicità 3.

Consideriamo ora una “funzione di linea”:

��+��+�=0

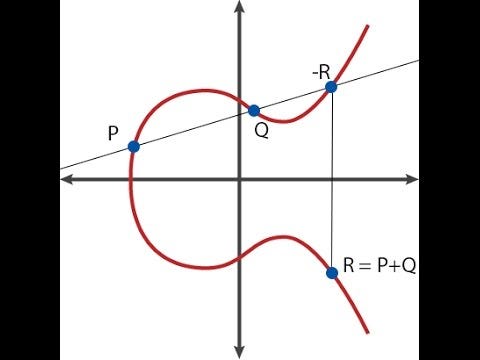
Dove �, � e � sono scelti attentamente in modo che la retta passi per i punti � e �. A causa del modo in cui funziona l'addizione della curva ellittica (vedere il diagramma in alto), ciò significa anche che passa per −�−�. E va fino all'infinito in base sia a � che a �, quindi il divisore diventa [�]+[�]+[−�−�]−3⋅[�].

Sappiamo che ogni “funzione razionale” (cioè una funzione definita solo utilizzando un numero finito di operazioni +,−,⋅ e / sulle coordinate del punto) corrisponde univocamente a qualche divisore, fino alla moltiplicazione per una costante (es. se due funzioni � e � hanno lo stesso divisore, allora �=�⋅� per qualche costante �).

Per due funzioni qualsiasi � e �, il divisore di �⋅� è uguale al divisore di � più il divisore di � (nei libri di testo di matematica, vedrai (�⋅�)=(�)+(�)), quindi ad esempio se �(�,�)=��−�, allora (�3)=3⋅[�]+3⋅[−�]−6⋅[�]; � e −� vengono “conteggiati tre volte” per tenere conto del fatto che �3 si avvicina a 0 in quei punti “tre volte più velocemente” in un certo senso matematico.

Nota che esiste un teorema che afferma che se “rimuovi le parentesi quadre” da un divisore di una funzione, la somma dei punti deve dare: �([�]+[�]+[−�−�]−3⋅[ �] si adatta chiaramente, come �+�−�−�−3⋅�=�), e qualsiasi divisore che abbia questa proprietà è il divisore di una funzione.

Ora siamo pronti per esaminare gli abbinamenti Tate. Consideriamo le seguenti funzioni, definite tramite i loro divisori:

• (��)=�⋅[�]−�⋅[�], dove � è l'ordine di �1, cioè. �⋅�=� per qualsiasi �
• (��)=�⋅[�]−�⋅[�]
• (�)=[�+�]−[�]−[�]+[�]

Ora diamo un'occhiata al prodotto ��⋅��⋅��. Il divisore è:

�⋅[�]−�⋅[�]+�⋅[�]−�⋅[�]+�⋅[�+�]−�⋅[�]−�⋅[�]+�⋅[�]

Il che si semplifica nettamente in:

�⋅[�+�]−�⋅[�]

Si noti che questo divisore ha esattamente lo stesso formato del divisore per �� e �� sopra. Quindi, ��⋅��⋅��=��+�.

Ora introduciamo una procedura chiamata passaggio di “esponenziazione finale”, in cui prendiamo il risultato delle nostre funzioni sopra (��,��, ecc.) e lo eleviamo alla potenza �=(�12−1)/�, dove �12−1 è l'ordine del gruppo moltiplicativo in (��)12 (cioè per in qualsiasi �∈(��)12,�(�12−1)=1). Nota che se applichi questa esponenziazione a qualsiasi risultato che abbia già stato elevato alla potenza di �, si ottiene un esponenziale alla potenza di �12−1, quindi il risultato diventa 1. Quindi, dopo l'elevamento a potenza finale, �� si annulla e otteniamo ���⋅���=( ��+�)�. C'è una certa bilinearità per te.

Ora, se vuoi creare una funzione che sia bilineare in entrambi gli argomenti, devi addentrarti in una matematica più spettrale, dove invece di prendere direttamente �� di un valore, prendi �� di a divisore, ed è da qui che nasce l'intero "abbinamento Tate". Per dimostrare altri risultati bisogna avere a che fare con nozioni come “equivalenza lineare” e “reciprocità di Weil”, e la tana del coniglio continua da lì. Puoi trovare altro materiale di lettura su tutto questo qui ed qui.

Per un'implementazione di una versione modificata dell'accoppiamento Tate, chiamato accoppiamento Ate ottimale, Vedere qui. Il codice implementa Algoritmo di Miller, che è necessario per calcolare effettivamente ��.

Si noti che il fatto che accoppiamenti come questo siano possibili è in qualche modo una benedizione: da un lato, significa che tutti i protocolli che possiamo fare con gli accoppiamenti diventano possibili, ma significa anche che dobbiamo stare più attenti a quali curve ellittiche noi usiamo.

Ogni curva ellittica ha un valore chiamato an grado di incorporamento; essenzialmente, il più piccolo � tale che ��−1 sia un multiplo di � (dove � è il primo utilizzato per il campo e �� è l’ordine della curva). Nei campi sopra, �=12, e nei campi utilizzati per l'ECC tradizionale (cioè dove non ci interessano gli accoppiamenti), il grado di incorporamento è spesso estremamente ampio, al punto che gli accoppiamenti sono computazionalmente impossibili da calcolare; tuttavia, se non stiamo attenti, possiamo generare campi dove �=4 o anche 1.

Se �=1, allora il problema del “logaritmo discreto” per le curve ellittiche (in sostanza, recuperando � conoscendo solo il punto �=�⋅�, il problema che bisogna risolvere per “craccare” una chiave privata della curva ellittica) può essere ridotto in un problema di matematica simile su ��, dove il problema diventa molto più semplice (questo è chiamato the Attacco MOV); l'utilizzo di curve con un grado di incorporamento pari a 12 o superiore garantisce che questa riduzione non sia disponibile o che risolvere il problema del registro discreto sui risultati dell'accoppiamento sia difficile almeno quanto recuperare una chiave privata da una chiave pubblica "nel modo normale" (ovvero. computazionalmente irrealizzabile). Non preoccuparti; tutti i parametri della curva standard sono stati accuratamente controllati per questo problema.

Resta sintonizzato per una spiegazione matematica di come funzionano zk-SNARK, disponibile a breve.

Un ringraziamento speciale a Christian Reitwiessner, Ariel Gabizon (di Zcash) e Alfred Menezes per la revisione e le correzioni.

• Distribuzione di contenuti basati su SEO e PR. Ricevi amplificazione oggi.
• PlatoData.Network Generativo verticale Ai. Potenzia te stesso. Accedi qui.
• PlatoAiStream. Intelligenza Web3. Conoscenza amplificata. Accedi qui.
• PlatoneESG. Carbonio, Tecnologia pulita, Energia, Ambiente, Solare, Gestione dei rifiuti. Accedi qui.
• Platone Salute. Intelligence sulle biotecnologie e sulle sperimentazioni cliniche. Accedi qui.
• BlockOffset. Modernizzare la proprietà della compensazione ambientale. Accedi qui.
• Fonte: Platone Data Intelligence.