Introduzione
In questo articolo esploreremo di cosa si tratta verifica di ipotesi, concentrandoci sulla formulazione di ipotesi nulle e alternative, impostando test di ipotesi e approfondiremo i test parametrici e non parametrici, discutendo le rispettive ipotesi e l'implementazione in Python. Ma il nostro focus principale sarà sui test non parametrici come il test U di Mann-Whitney e il test Kruskal-Wallis. Alla fine, avrai una conoscenza completa del test delle ipotesi e degli strumenti pratici per applicare questi concetti nelle tue analisi statistiche.
obiettivi formativi
- Comprendere i principi della verifica delle ipotesi, inclusa la formulazione di ipotesi nulle e alternative.
- Impostazione del test di ipotesi.
- Comprensione del test parametrico e delle sue tipologie.
- Comprensione dei test non parametrici e dei suoi tipi insieme alle sue implementazioni.
- Differenza tra parametrico e non parametrico.
Sommario
Cos'è il test di ipotesi?
L'ipotesi è un'affermazione fatta da una persona/organizzazione. L'affermazione riguarda solitamente parametri della popolazione come la media o la proporzione e cerchiamo prove da un campione a sostegno dell'affermazione.
Il test di ipotesi, a volte indicato come test di significatività, è un metodo per confermare un'affermazione o un'ipotesi su un parametro in una popolazione utilizzando i dati misurati in un campione. Utilizzando questo metodo, esploriamo diverse teorie determinando la possibilità che, se l'ipotesi del parametro della popolazione fosse stata vera, sarebbe stato selezionato un campione statistico.
Il test delle ipotesi prevede la formulazione di due ipotesi:
- Ipotesi nulla (H0)
- Ipotesi alternativa (H1)
Ipotesi nulla : Di solito è un'ipotesi senza differenza e solitamente indicata con H0. Secondo RA Fisher, l'ipotesi nulla è l'ipotesi che viene testata per un possibile rifiuto partendo dal presupposto che sia vera (Rif Fondamenti di statistica matematica).
Ipotesi alternativa: Qualsiasi ipotesi complementare all'ipotesi nulla è chiamata ipotesi alternativa, solitamente indicata con H1.
L'obiettivo del test delle ipotesi è rifiutare o mantenere un'ipotesi nulla per stabilire una relazione statisticamente significativa tra due variabili (solitamente una variabile indipendente e una variabile dipendente, ovvero solitamente una è la causa e l'altra l'effetto).
Impostazione del test di ipotesi
- Descrivi l'ipotesi a parole o fai un'affermazione.
- Sulla base del reclamo definire ipotesi nulle e alternative.
- Identificare il tipo di test di ipotesi appropriato per l'affermazione di cui sopra.
- Identificare le statistiche di test da utilizzare per verificare la validità dell'ipotesi nulla.
- Decidere i criteri per il rifiuto e il mantenimento dell'ipotesi nulla. Questo è chiamato valore di significatività tradizionalmente indicato con il simbolo α (alfa).
- Calcolare il valore p che è la probabilità condizionata di osservare il valore statistico del test quando l'ipotesi nulla è vera. In termini semplici, il valore p è la prova a sostegno dell’ipotesi nulla.
Test parametrici e non parametrici
I test statistici non parametrici non si basano su ipotesi sui parametri delle distribuzioni della popolazione da cui vengono campionati i dati, mentre i test statistici parametrici sì.
Prove parametriche
La maggior parte dei test statistici vengono eseguiti utilizzando una serie di ipotesi come fondamento. L'analisi può portare a conclusioni fuorvianti o completamente false quando vengono violati determinati presupposti.
Solitamente le ipotesi sono:
- Normalità: la distribuzione campionaria dei parametri da testare segue una distribuzione normale (o almeno simmetrica).
- Omogeneità delle varianze: la varianza dei dati è la stessa tra gruppi diversi a meno che non stiamo testando le medie della popolazione provenienti da due popolazioni diverse.
Alcuni dei test parametrici sono:
- Test Z: Test per la media, la varianza o la proporzione della popolazione quando la deviazione standard della popolazione è nota.
- Test t di Student: Test per la media, la varianza o la proporzione della popolazione quando la deviazione standard della popolazione non è nota.
- Test t accoppiato: Utilizzato per confrontare le medie di due gruppi o condizioni correlati.
- Analisi della varianza (ANOVA): Utilizzato per confrontare le medie di tre o più gruppi indipendenti.
- Analisi di regressione: Utilizzato per valutare la relazione tra una o più variabili indipendenti e una variabile dipendente.
- Analisi della Covarianza (ANCOVA): Estende ANOVA incorporando covariate aggiuntive nell'analisi.
- Analisi multivariata della varianza (MANOVA): Estende ANOVA per valutare le differenze in più variabili dipendenti tra i gruppi.
Ora approfondiamo il test non parametrico.
Test non parametrico
Per la prima volta Wolfowitz usò il termine “non parametrico” nel 1942. Per comprendere il concetto di statistica non parametrica, è necessario prima avere una conoscenza di base della statistica parametrica, di cui abbiamo appena discusso. UN prova parametrica richiede un campione che segua una distribuzione specifica (solitamente normale). Inoltre, i test non parametrici sono indipendenti da presupposti parametrici come la normalità.
Test non parametrici (noti anche come test senza distribuzione poiché non hanno ipotesi sulla distribuzione della popolazione). I test non parametrici implicano che i test non si basano sul presupposto che i dati siano tratti da a distribuzione di probabilità definita attraverso parametri quali media, proporzione e deviazione standard.
I test non parametrici vengono utilizzati quando:
- Il test non riguarda i parametri della popolazione come la media o la proporzione.
- Il metodo non richiede ipotesi sulla distribuzione della popolazione (ad esempio, la popolazione segue una distribuzione normale).
Tipi di test non parametrici
Ora discutiamo il concetto e la procedura per eseguire il test Chi-quadrato, il test di Mann-Whitney, il test dei gradi firmati di Wilcoxon e i test di Kruskal-Wallis:
Test Chi-quadrato
Per determinare se l'associazione tra due variabili qualitative è statisticamente significativa, è necessario condurre un test di significatività chiamato test del Chi-quadrato.
Esistono due tipi principali di test Chi-quadrato:
Bontà di adattamento del chi quadrato
Utilizzare il test della bontà di adattamento per decidere se una popolazione con una distribuzione sconosciuta “si adatta” a una distribuzione nota. In questo caso ci sarà una singola domanda di indagine qualitativa o un singolo risultato di un esperimento da una singola popolazione. La bontà dell'adattamento viene in genere utilizzata per verificare se la popolazione è uniforme (tutti i risultati si verificano con la stessa frequenza), la popolazione è normale o la popolazione è uguale a un'altra popolazione con una distribuzione nota. Le ipotesi nulla e alternativa sono:
- H0: La popolazione si adatta alla distribuzione data.
- Ha: La popolazione non rientra nella distribuzione data.
Capiamolo con un esempio
| Giorni | Lunedì | Martedì | Mercoledì | Giovedì | Venerdì | Sabato | Domenica |
| Numero di guasti | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
La tabella mostra il numero di ripartizioni in un fattore. In questo esempio è presente solo una singola variabile e dobbiamo determinare se la distribuzione osservata (fornita nella tabella) si adatta o meno alla distribuzione prevista.
Per questo l’ipotesi nulla e l’ipotesi alternativa saranno formulate come:
- H0:Le ripartizioni sono distribuite uniformemente.
- Ha: I guasti non sono distribuiti uniformemente.
E il grado di libertà sarà n-1 (in questo caso n=7, quindi df = 7-1=6)
Expected value will be= (14+22+16+18+12+19+11)/7=16
| Giorni | Lunedì | Martedì | Mercoledì | Giovedì | Venerdì | Sabato | Domenica |
| Numero di guasti (osservati) | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
| previsto | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| (osservato-atteso) | -2 | 6 | 0 | 2 | -4 | 3 | -5 |
| (osservato-atteso)^2 | 4 | 36 | 0 | 4 | 16 | 9 | 25 |
Utilizzando questa formula Calcola il Chi-quadrato
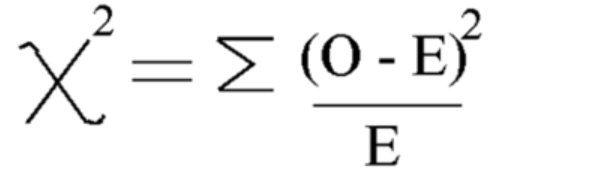
Chi quadrato = 5.875
E il grado di libertà è = n-1=7-1=6
Ora vediamo il valore critico da tabella di distribuzione del chi quadrato con un livello di significatività del 5%.
Quindi il valore critico è 12.592
Poiché il valore calcolato del Chi-quadrato è inferiore al valore critico, accettiamo l'ipotesi nulla e possiamo concludere che le ripartizioni sono distribuite uniformemente.
Indipendenza del test chi-quadrato
Utilizzare il test di indipendenza per decidere se due variabili (fattori) sono indipendenti o dipendenti, cioè se queste due variabili hanno o meno una relazione di associazione significativa tra loro. In questo caso ci saranno due domande o esperimenti di indagine qualitativa e verrà costruita una tabella di contingenza. L'obiettivo è vedere se le due variabili sono non correlate (indipendenti) o correlate (dipendenti). Le ipotesi nulla e alternativa sono:
- H0: Le due variabili (fattori) sono indipendenti.
- Ha: Le due variabili (fattori) sono dipendenti.
Facciamo un esempio
Esempio in cui vogliamo indagare se il genere e il colore preferito della maglietta fossero indipendenti. Ciò significa che vogliamo scoprire se il genere di una persona influenza la scelta del colore. Abbiamo condotto un sondaggio e organizzato i dati nella tabella.
Questa tabella riporta i valori osservati:
| Nero | White | Rosso | Blu | |
| Uomo | 48 | 12 | 33 | 57 |
| Femmili | 34 | 46 | 42 | 26 |
Ora formuliamo prima ipotesi nulle e alternative
- H0: Il sesso e il colore preferito della maglietta sono indipendenti
- Ha: Il sesso e il colore preferito della maglietta non sono indipendenti
Per calcolare le statistiche del test Chi quadrato dobbiamo calcolare il valore atteso. Quindi, aggiungi tutte le righe e le colonne e i totali complessivi:
| Nero | White | Rosso | Blu | Totale | |
| Uomo | 48 | 12 | 33 | 57 | 150 |
| Femmili | 34 | 46 | 42 | 26 | 148 |
| Totale | 82 | 58 | 75 | 83 | 298 |
Successivamente possiamo calcolare la tabella dei valori attesi dalla tabella sopra per ciascuna voce utilizzando questa formula = (totale riga * totale colonna)/totale complessivo
Tabella dei valori attesi:
| Nero | White | Rosso | Blu | |
| Uomo | 41.3 | 29.2 | 37.8 | 41.8 |
| Femmili | 40.7 | 28.8 | 37.2 | 41.2 |
Ora calcola il valore del Chi quadrato utilizzando la formula per il test chi quadrato:
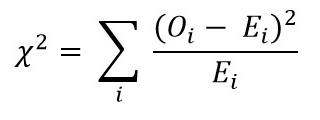
- Oi = Valore osservato
- Ei = Valore atteso
Il valore che otteniamo è: Χ2 = 34.9572
Calcola il grado di libertà
DF=(numero di riga-1)*(numero di colonna-1)
Ora trova e confronta il valore critico con il test chi-quadrato valore statistico:
Per fare ciò puoi cercare il grado di libertà e il livello di significatività (alfa) da tabella di distribuzione chi-quadrato
Con alfa = 0.050, otterremo un valore critico = 7.815
Poiché chi-quadrato> valore critico
Pertanto, rifiutiamo l’ipotesi nulla e possiamo concludere che il genere e il colore preferito della maglietta non sono indipendenti.
Implementazione del Chi-Quadro
Ora, vediamo l'implementazione di Chi-Square usando alcuni esempi di vita reale in Python:
- H0: Il sesso e il colore preferito della maglietta sono indipendenti
- Ha: Il sesso e il colore preferito della maglietta non sono indipendenti
Creazione del set di dati:
import pandas as pd
from scipy.stats import chi2_contingency
from scipy.stats import chi2
# Given dataset
df_dict = {
'Black': [48, 34],
'White': [12, 46],
'Red': [33, 42],
'Blue': [57, 26]
}
dataset_table = pd.DataFrame(df_dict, index=['Male', 'Female'])
print("Dataset Table:")
print(dataset_table)
print()
# Observed Values
Observed_Values = dataset_table.values
print("Observed Values:")
print(Observed_Values)
print()
# Perform chi-square test
val = chi2_contingency(dataset_table)
Expected_Values = val[3]
print("Expected Values:")
print(Expected_Values)
print()
# Degree of Freedom
no_of_rows = len(dataset_table.iloc[0:2, 0])
no_of_columns = 4
ddof = (no_of_rows - 1) * (no_of_columns - 1)
print("Degree of Freedom:", ddof)
print()
# Chi-square statistic
chi_square = sum([(o - e) ** 2. / e for o, e in zip(Observed_Values, Expected_Values)])
chi_square_statistic = chi_square[0] + chi_square[1]
print("Chi-square statistic:", chi_square_statistic)
print()
# Critical value
alpha = 0.05
critical_value = chi2.ppf(q=1-alpha, df=ddof)
print('Critical value:', critical_value)
print()
# p-value
p_value = 1 - chi2.cdf(x=chi_square_statistic, df=ddof)
print('p-value:', p_value)
print()
# Significance level
print('Significance level:', alpha)
print('p-value:', p_value)
print('Degree of Freedom:', ddof)
print()
# Hypothesis testing
if chi_square_statistic >= critical_value:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
print()
if p_value <= alpha:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
Produzione:
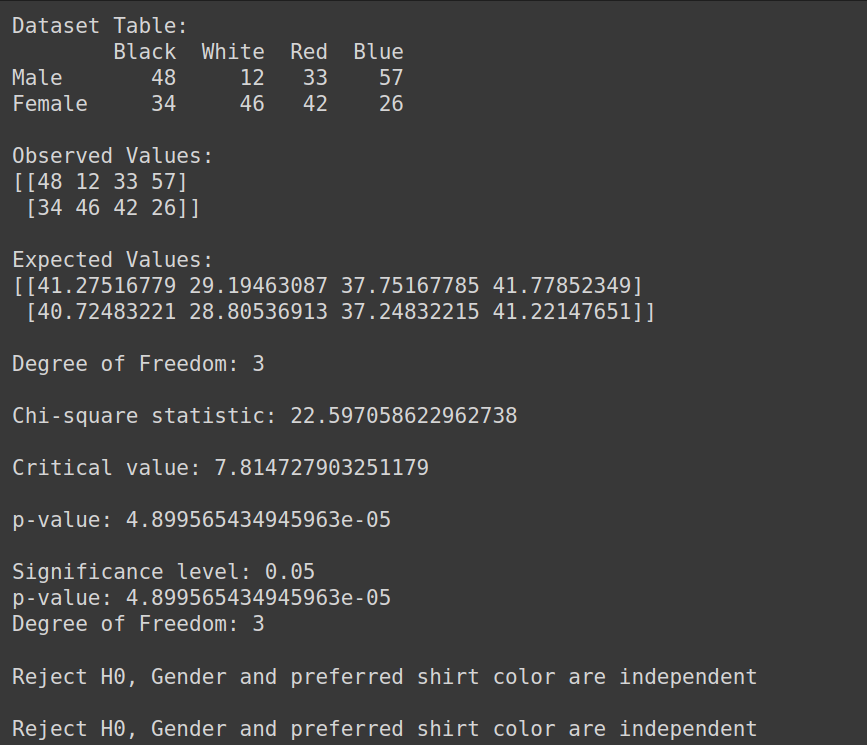
Test U di Mann-Whitney
Il test U di Mann-Whitney funge da alternativa non parametrica al test t del campione indipendente. Confronta due medie campionarie della stessa popolazione, determinando se sono uguali. Questo test viene generalmente utilizzato per dati ordinali o quando le ipotesi del test t non sono soddisfatte.
Il test U di Mann-Whitney classifica insieme tutti i valori di entrambi i gruppi, quindi somma i ranghi per ciascun gruppo. Calcola la statistica del test, U, in base a questi ranghi. La statistica U viene confrontata con un valore critico da una tabella o calcolata utilizzando un'approssimazione. Se la statistica U è inferiore al valore critico, l’ipotesi nulla viene rifiutata.
Questo è diverso dai test parametrici come il test t, che confrontano le medie e presuppongono una distribuzione normale. Il test U di Mann-Whitney confronta invece i ranghi e non richiede l'assunzione di una distribuzione normale.
Comprendere il test U di Mann-Whitney può essere difficile perché i risultati sono presentati in differenze di rango di gruppo piuttosto che in differenze medie di gruppo.
Formula per il test di Mann-Whitney:
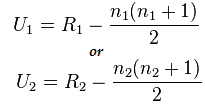
U=min(U1,U2)
Qui,
- U=Test U di Mann-Whitney
- n1= dimensione del campione uno
- n2=dimensione del campione due
- R1= Rango della dimensione del campione uno
- R2= Rango della dimensione del campione 2
Allora, capiamolo con un breve esempio:
Supponiamo di voler confrontare l'efficacia di due diversi metodi di trattamento (Metodo A e Metodo B) nel migliorare la salute dei pazienti. Disponiamo dei seguenti dati:
- Metodo A: 3,4,2,6,2,5
- Metodo B: 9,7,5,10,6,8
Qui possiamo vedere che i dati non sono distribuiti normalmente e le dimensioni del campione sono piccole.
Implementazione del test U di Mann-Whitney
Ora eseguiamo il test U di Mann-Whitney:
Ma prima formuliamo l'ipotesi Nulla e Alternativa
- H0: Non c'è differenza tra il Grado di ciascun trattamento
- Ha: C'è una differenza tra il Grado di ciascun trattamento
Combina tutti i trattamenti: 3,4,2,6,2,5,9,7,5,10,6,8
Dati ordinati: 2,2,3,4,5,5,6,6,7,8,9,10
Rango dei dati ordinati: 1,2,3,4,5,6,7,8,9,10,11,12
- Classificare i dati separatamente:
- Method A: 3(3),4(4),2(1.5),6(7.5),2(1.5),5(5.5)
- Method B: 9(11),7(9),5(5.5),10(12),6(1.5),8(10)
- Calcolo della somma del rango):
- R1: 3+4+1.5+7.5+1.5+5.5=23
- R2: 11+9+5.5+12+1.5+10=55
Ora calcola il valore statistico utilizzando questa formula:
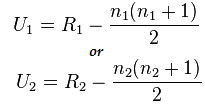
Qui n1=6 e n2=6
E il valore dopo il calcolo per U1=2 e per U2= 34
Calcolo della statistica U:
Us= min(U1,U2)= min(2,34)= 2
Da Tavolo Mann-Whitney possiamo trovare il valore critico
In questo caso il Valore Critico sarà 5
Poiché Uc= 5 che è maggiore di Us al livello di significatività del 5%, quindi rifiutiamo H0
Possiamo quindi concludere che esiste una differenza tra il Rank di ciascun trattamento.
Implementazione con Python
from scipy.stats import mannwhitneyu, norm
import numpy as np
TreatmentA = np.array([3,4,2,6,2,5])
TreatmentB = np.array([9,7,5,10,6,8])
# Perform Mann-Whitney U test
U_statistic, p_value = mannwhitneyu(TreatmentA, TreatmentB)
# Print the result
print(f'The U-statistic is {U_statistic:.2f} and the p-value is {p_value:.4f}')
if p_value < 0.05:
print("Reject Null Hypothesis: There is a significant difference between the Rank of each treatment.")
else:
print("Fail to Reject Null Hypothesis: Fail to Reject Null Hypothesis: There is no enough evidence to conclude that there is difference between the Rank of each treatment")Produzione:

Test di Kruskal-Wallis
Il test Kruskal –Wallis viene utilizzato con più gruppi. È un'alternativa non parametrica e valida al test ANOVA unidirezionale quando vengono violate le ipotesi di normalità e uguaglianza della varianza. Il test Kruskal-Wallis confronta le mediane di più di due gruppi indipendenti.
Verifica l'ipotesi nulla quando k campioni indipendenti (k>=3) vengono estratti da una popolazione con distribuzioni identiche, senza richiedere la condizione di normalità per le popolazioni.
Ipotesi:
Assicurarsi che vi siano almeno tre campioni casuali estratti in modo indipendente. Ogni campione ha almeno 5 osservazioni, n>=5
Consideriamo un esempio in cui vogliamo determinare se la tecnica di studio utilizzata da tre gruppi di studenti influisce sui punteggi degli esami. Possiamo utilizzare il test Kruskal-Wallis per analizzare i dati e valutare se ci sono differenze statisticamente significative nei punteggi degli esami tra i gruppi.
Formulare l'ipotesi nulla per questo come:
- H0: Non c'è differenza nei punteggi degli esami tra i tre gruppi di studenti.
- Ha: C'è una differenza nei punteggi degli esami tra i tre gruppi di studenti.
Test di grado firmato Wilcoxon
Il Wilcoxon Signed Rank Test (noto anche come Wilcoxon Matched Pair Test) è la versione non parametrica del t-test del campione dipendente o del t-test del campione appaiato. Il test dei segni è l'altra alternativa non parametrica al test t per campioni appaiati. Viene utilizzato quando le variabili di interesse sono di natura dicotomica (come Maschio e Femmina, Sì e No). Il test dei ranghi firmati di Wilcoxon è anche una versione non parametrica per il test t di un campione. Il Wilcoxon Signed Rank Test confronta le mediane dei gruppi in due situazioni (campioni accoppiati) oppure confronta la mediana del gruppo con la mediana ipotizzata (un campione).
Capiamolo con un esempio: supponiamo di avere dati sul consumo giornaliero di sigarette dei fumatori prima e dopo la partecipazione a un programma di 8 settimane e vogliamo determinare se c'è una differenza significativa nel consumo giornaliero di sigarette prima e dopo il programma, allora lo faremo usa questo test
La formulazione dell'ipotesi per questo sarà
- H0: Non vi è alcuna differenza nel consumo quotidiano di sigarette prima e dopo il programma.
- Ha: C'è una differenza nel consumo quotidiano di sigarette prima e dopo il programma
Prova per la normalità
Parliamo ora dei test di normalità:
Test di Shapiro Wilk
Il test di Shapiro-Wilk valuta se un dato campione di dati proviene da una popolazione distribuita normalmente. È uno dei test più comunemente utilizzati per verificare la normalità. Il test è particolarmente utile quando si ha a che fare con campioni di dimensioni relativamente piccole.
Nel test di Shapiro-Wilk:
- Ipotesi nulla : I dati del campione provengono da una popolazione che segue una distribuzione normale.
- Ipotesi alternativa : I dati del campione non provengono da una popolazione che segue una distribuzione normale.
La statistica del test generata dal test di Shapiro-Wilk misura la discrepanza tra i dati osservati e i dati attesi presupponendo la normalità. Se il valore p associato alla statistica test è inferiore al livello di significatività scelto (ad esempio, 0.05), rifiutiamo l'ipotesi nulla, indicando che i dati non sono distribuiti normalmente. Se il valore p è maggiore del livello di significatività, non riusciamo a rifiutare l'ipotesi nulla, suggerendo che i dati potrebbero seguire una distribuzione normale.
Per prima cosa creiamo un set di dati per questi test, puoi utilizzare qualsiasi set di dati di tua scelta:
import pandas as pd
# Create the dictionary with the provided data
data = {
'population': [6.1101, 5.5277, 8.5186, 7.0032, 5.8598],
'profit': [17.5920, 9.1302, 13.6620, 11.8540, 6.8233]
}
# Create the DataFrame
df = pd.DataFrame(data)
response_var=df['profit']
Here, a sample for running Shapiro -Wilk test on python:
from scipy.stats import shapiro
stat, p_val = shapiro(response_var)
print(f'Shapiro-Wilk Test: Statistic={stat} p-value={p_val}')
if p_val > alpha:
print('Data looks normal (fail to reject H0)')
else:
print('Data looks normal (fail to reject H0)')Produzione:

Questo test è più appropriato per campioni di dimensioni relativamente piccole (n=< 50-2000) poiché diventa meno affidabile con campioni di dimensioni maggiori.
Anderson-Darling
Valuta se un dato campione di dati proviene da una distribuzione specifica, come la distribuzione normale. È simile al test di Shapiro-Wilk ma è più sensibile soprattutto per campioni di piccole dimensioni.
È adatto a diverse distribuzioni, inclusa la distribuzione normale, per i casi in cui i parametri della distribuzione sono sconosciuti.
Qui, il codice Python per implementarlo:
from scipy.stats import anderson
response_var = data['profit']
alpha = 0.05
# Anderson-Darling Test
result = anderson(response_var)
print(f'Anderson statistics: {result.statistic:.3f}')
if result.statistic > result.critical_values[-1]:
p_value = 0.0 # The p-value is essentially 0 if the statistic exceeds the largest critical value
else:
p_value = result.significance_level[result.statistic < result.critical_values][-1]
print("P-value:", p_value)
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")Produzione:

Test di Jarque-Bera
Il test Jarque-Bera valuta se un dato campione di dati proviene da una popolazione distribuita normalmente. Si basa sull'asimmetria e sulla curtosi dei dati.
Ecco l'implementazione di Jarque-Bera Test in Python con dati di esempio:
from scipy.stats import jarque_bera
# Performing Jarque-Bera test
test_statistic, p_value = jarque_bera(response_var)
print("Jarque-Bera Test Statistic:", test_statistic)
print("P-value:", p_value)
# Interpreting results
alpha = 0.05
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")Produzione:

| Categoria | Tecniche statistiche parametriche | Statistica non parametricatecniche |
| correlazione | Coefficiente di correlazione momento prodotto Pearson (r) | Correlazione del coefficiente di rango di Spearman (Rho), Tau di Kendall |
| Due gruppi, misure indipendenti | Test t indipendente | Test U di Mann-Whitney |
| Più di due gruppi, misure indipendenti | ANOVA a senso unico | ANOVA unidirezionale Kruskal-Wallis |
| Due gruppi, misure ripetute | Test t accoppiato | Test di grado firmato per coppia abbinata di Wilcoxon |
| Più di due gruppi, misure ripetute | ANOVA a misure ripetute unidirezionali | Analisi della varianza a due vie di Friedman |
Conclusione
Verifica di ipotesi è essenziale per valutare le affermazioni sui parametri della popolazione utilizzando dati campione. I test parametrici si basano su presupposti specifici e sono adatti per dati su intervalli o rapporti, mentre i test non parametrici sono più flessibili e applicabili a dati nominali o ordinali senza rigidi presupposti distribuzionali. Test come Shapiro-Wilk e Anderson-Darling valutano la normalità, mentre Chi-quadrato e Jarque-Bera valutano la bontà dell'adattamento. Comprendere le differenze tra test parametrici e non parametrici è fondamentale per selezionare l'approccio statistico appropriato. Nel complesso, la verifica delle ipotesi fornisce un quadro sistematico per prendere decisioni basate sui dati e trarre conclusioni affidabili da prove empiriche.
Pronto a padroneggiare l'analisi statistica avanzata? Iscriviti oggi stesso al nostro corso di analisi dei dati BlackBelt! Acquisisci esperienza nel test di ipotesi, test parametrici e non parametrici, implementazione Python e altro ancora. Migliora le tue capacità statistiche ed eccelle nel processo decisionale basato sui dati. Iscriviti adesso!
Domande frequenti
A. I test parametrici fanno ipotesi sulla distribuzione della popolazione e sui parametri, come la normalità e l'omogeneità della varianza, mentre i test non parametrici non si basano su queste ipotesi. I test parametrici hanno più potere quando vengono soddisfatte le ipotesi, mentre i test non parametrici sono più robusti e applicabili in una gamma più ampia di situazioni, incluso quando i dati sono distorti o non distribuiti normalmente.
A. Il test chi quadrato viene utilizzato per determinare se esiste un'associazione significativa tra due variabili categoriali. Di solito analizza dati categorici e verifica ipotesi sull'indipendenza delle variabili nelle tabelle di contingenza.
A. Il test U di Mann-Whitney confronta due gruppi indipendenti quando la variabile dipendente è ordinale o non distribuita normalmente. Si valuta se esiste una differenza significativa tra le mediane dei due gruppi.
R. Il test di Shapiro-Wilk valuta se un campione proviene da una popolazione distribuita normalmente. Verifica l'ipotesi nulla che i dati seguano una distribuzione normale. Se il valore p è inferiore al livello di significatività scelto (ad esempio, 0.05), rifiutiamo l'ipotesi nulla, concludendo che i dati non sono distribuiti normalmente.
- Distribuzione di contenuti basati su SEO e PR. Ricevi amplificazione oggi.
- PlatoData.Network Generativo verticale Ai. Potenzia te stesso. Accedi qui.
- PlatoAiStream. Intelligenza Web3. Conoscenza amplificata. Accedi qui.
- PlatoneESG. Carbonio, Tecnologia pulita, Energia, Ambiente, Solare, Gestione dei rifiuti. Accedi qui.
- Platone Salute. Intelligence sulle biotecnologie e sulle sperimentazioni cliniche. Accedi qui.
- Fonte: https://www.analyticsvidhya.com/blog/2024/04/a-comprehensive-guide-on-non-parametric-tests/



