Les informaticiens sont des gens exigeants. Pour eux, il ne suffit pas d'obtenir la bonne réponse à un problème : l'objectif, presque toujours, est d'obtenir la réponse aussi efficacement que possible.

Prenez l'acte de multiplier des matrices ou des tableaux de nombres. En 1812, le mathématicien français Jacques Philippe Marie Binet a proposé l'ensemble des règles de base que nous enseignons encore aux étudiants. Cela fonctionne parfaitement, mais d’autres mathématiciens ont trouvé des moyens de simplifier et d’accélérer le processus. Maintenant la tâche de accélérer le processus La multiplication matricielle se situe à l’intersection des mathématiques et de l’informatique, où les chercheurs continuent d’améliorer le processus à ce jour – même si au cours des dernières décennies, les progrès ont été assez modestes. Depuis 1987, les améliorations numériques dans la multiplication matricielle ont été « minimes et… extrêmement difficiles à obtenir », a déclaré François Le Gall, informaticien à l'Université de Nagoya.

Aujourd’hui, trois chercheurs – Ran Duan et Renfei Zhou de l’Université Tsinghua et Hongxun Wu de l’Université de Californie à Berkeley – ont fait un grand pas en avant dans la lutte contre ce problème éternel. Leur nouveaux résultats, présentés en novembre dernier lors de la conférence Foundations of Computer Science, découlent d'une nouvelle technique inattendue, a déclaré Le Gall. Bien que l’amélioration elle-même soit relativement faible, Le Gall la qualifie de « conceptuellement plus grande que les autres précédentes ».

La technique révèle une source d’améliorations potentielles jusqu’alors inconnue et donc inexploitée, et elle a déjà porté ses fruits : Un deuxième papier, publié en janvier, s'appuie sur le premier pour montrer comment la multiplication matricielle peut être encore améliorée.

"Il s'agit d'une avancée technique majeure", a déclaré William Kuszmaul, informaticien théorique à l'Université Harvard. "Il s'agit de la plus grande amélioration en matière de multiplication matricielle que nous ayons vue depuis plus d'une décennie."

Entrez la matrice

Cela peut sembler un problème obscur, mais la multiplication matricielle est une opération informatique fondamentale. Il est intégré dans une grande partie des algorithmes que les gens utilisent quotidiennement pour diverses tâches, depuis l'affichage d'infographies plus nettes jusqu'à la résolution de problèmes logistiques liés à la théorie des réseaux. Et comme dans d’autres domaines du calcul, la vitesse est primordiale. Même de légères améliorations pourraient éventuellement conduire à des économies significatives de temps, de puissance de calcul et d’argent. Mais pour l’instant, les théoriciens s’intéressent principalement à la vitesse à laquelle le processus pourra jamais se dérouler.

La manière traditionnelle de multiplier deux nParn matrices - en multipliant les nombres de chaque ligne de la première matrice par les nombres des colonnes de la seconde - nécessite n³ multiplications séparées. Pour les matrices 2x2, cela signifie 2³ ou 8 multiplications.

En 1969, le mathématicien Volker Strassen a révélé une procédure plus compliquée permettant de multiplier des matrices 2 par 2 en seulement sept étapes multiplicatives et 18 additions. Deux ans plus tard, l'informaticien Shmuel Winograd démontrait que sept est effectivement le minimum absolu pour les matrices 2 x 2.

Strassen a exploité cette même idée pour montrer que toutes les nParn les matrices peuvent également être multipliées en moins de n³ pas. Un élément clé de cette stratégie implique une procédure appelée décomposition : décomposer une grande matrice en sous-matrices successivement plus petites, qui pourraient finir par être aussi petites que 2 sur 2 ou même 1 sur 1 (ce ne sont que des nombres simples).

La raison pour diviser un réseau géant en petits morceaux est assez simple, selon Virginie Vassilevska Williams, informaticien au Massachusetts Institute of Technology et co-auteur de l'un des nouveaux articles. "Il est difficile pour un humain de regarder une grande matrice (disons de l'ordre de 100 x 100) et de penser au meilleur algorithme possible", a déclaré Vassilevska Williams. Même les matrices 3x3 n'ont pas encore été entièrement résolues. "Néanmoins, on peut utiliser un algorithme rapide que l'on a déjà développé pour de petites matrices pour obtenir également un algorithme rapide pour des matrices plus grandes."

Les chercheurs ont déterminé que la clé de la rapidité est de réduire le nombre d'étapes de multiplication, en abaissant cet exposant de n³ (pour la méthode standard) autant qu'ils le peuvent. La valeur la plus basse possible, n², c'est fondamentalement le temps qu'il faut pour écrire la réponse. Les informaticiens appellent cet exposant oméga, ω, avec n^ω étant le moins d'étapes possibles nécessaires pour réussir à multiplier deux nParn matrices comme n devient très grand. "Le but de ce travail", a déclaré Zhou, qui a également co-écrit l'article de janvier 2024, "est de voir à quel point vous pouvez vous rapprocher de 2 et si cela peut être atteint en théorie."

Une mise au point laser

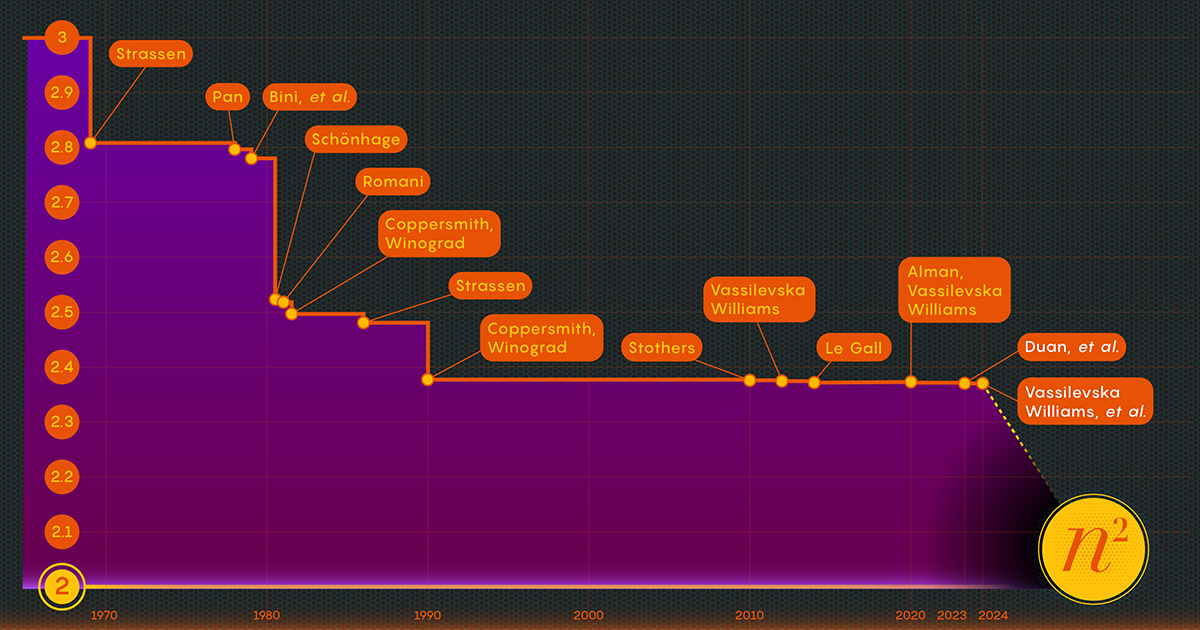
En 1986, Strassen réalise une autre grande percée en introduit ce qu'on appelle la méthode laser pour la multiplication matricielle. Strassen l'a utilisé pour établir une valeur supérieure pour les oméga de 2.48. Bien que la méthode ne soit qu’une étape dans les multiplications matricielles à grande échelle, elle est l’une des plus importantes car les chercheurs ont continué à l’améliorer.

Un an plus tard, Winograd et Don Coppersmith ont présenté un nouvel algorithme qui complétait à merveille la méthode laser. Cette combinaison d'outils a figuré dans pratiquement tous les efforts ultérieurs visant à accélérer la multiplication matricielle.

Voici une manière simplifiée de réfléchir à la façon dont ces différents éléments s’articulent. Commençons par deux grandes matrices, A et B, que vous souhaitez multiplier ensemble. Tout d’abord, vous les décomposez en plusieurs sous-matrices plus petites, ou blocs, comme on les appelle parfois. Ensuite, vous pouvez utiliser l'algorithme de Coppersmith et Winograd pour servir de sorte de manuel d'instructions pour la manipulation et finalement l'assemblage des blocs. "Cela me dit quoi multiplier, quoi ajouter et quelles entrées vont où" dans la matrice de produits C, a déclaré Vassilevska Williams. "C'est juste une recette pour construire C à partir de A et B."

Il y a cependant un problème : vous vous retrouvez parfois avec des blocs qui ont des entrées en commun. Les laisser dans le produit reviendrait à compter ces entrées deux fois, donc à un moment donné, vous devrez vous débarrasser de ces termes en double, appelés chevauchements. Pour ce faire, les chercheurs « tuent » les blocs dans lesquels ils se trouvent – ​​en définissant leurs composants égaux à zéro pour les supprimer du calcul.

C'est là que la méthode laser de Strassen entre enfin en jeu. "La méthode laser fonctionne généralement très bien et trouve généralement un bon moyen de tuer un sous-ensemble de blocs afin de supprimer le chevauchement", a déclaré Le Gall. Une fois que le laser a éliminé ou « brûlé » tous les chevauchements, vous pouvez construire la matrice du produit final, C.

La combinaison de ces différentes techniques aboutit à un algorithme permettant de multiplier deux matrices avec un nombre global de multiplications délibérément avare – du moins en théorie. La méthode laser n’est pas destinée à être pratique ; c'est juste une façon de réfléchir à la manière idéale de multiplier des matrices. "Nous n'exécutons jamais la méthode [sur un ordinateur]", a déclaré Zhou. "Nous l'analysons."

Et cette analyse est ce qui a conduit à la plus grande amélioration des oméga depuis plus d’une décennie.

Une perte est constatée

L'article de l'été dernier, rédigé par Duan, Zhou et Wu, montrait que le processus de Strassen pouvait encore être considérablement accéléré. Tout cela était dû à un concept qu’ils appelaient une perte cachée, profondément enfouie dans les analyses précédentes – « le résultat de la destruction involontaire d’un trop grand nombre de blocs », a déclaré Zhou.

La méthode laser fonctionne en étiquetant les blocs avec des chevauchements comme des déchets destinés à être éliminés ; les autres blocs sont jugés valables et seront sauvegardés. Le processus de sélection est cependant quelque peu aléatoire. Un bloc considéré comme un déchet peut, en fait, s'avérer utile après tout. Ce n'était pas une surprise totale, mais en examinant bon nombre de ces choix aléatoires, l'équipe de Duan a déterminé que la méthode laser sous-évaluait systématiquement les blocs : davantage de blocs devraient être conservés et moins jetés. Et comme c’est généralement le cas, moins de gaspillage se traduit par une plus grande efficacité.

"Le fait de pouvoir conserver plus de blocs sans chevauchement conduit ainsi à... un algorithme de multiplication matricielle plus rapide", a déclaré Le Gall.

Après avoir prouvé l'existence de cette perte, l'équipe de Duan a modifié la façon dont la méthode laser étiquetait les blocs, réduisant ainsi considérablement les déchets. En conséquence, ils ont fixé une nouvelle limite supérieure pour les oméga à environ 2.371866 – une amélioration par rapport à la précédente limite supérieure de 2.3728596. fixé en 2020 par Josh Alman et Vassilevska Williams. Cela peut sembler un changement modeste, puisqu’il abaisse la limite d’environ 0.001. Mais il s’agit de la plus grande amélioration observée par les scientifiques depuis 2010. En comparaison, le résultat de Vassilevska Williams et Alman pour 2020 n’a amélioré que 0.00001 par rapport à son prédécesseur.

Mais ce qui est le plus excitant pour les chercheurs, ce n'est pas seulement le nouveau record lui-même, qui n'a pas duré longtemps. C'est aussi que le journal révèle une nouvelle piste d'amélioration qui, jusqu'alors, était passée totalement inaperçue. Depuis près de quatre décennies, tout le monde s'appuie sur la même méthode laser, a déclaré Le Gall. "Ensuite, ils ont découvert que nous pouvions faire mieux."

L'article de janvier 2024 a affiné cette nouvelle approche, permettant à Vassilevska Williams, Zhou et leurs co-auteurs de réduire davantage la perte cachée. Cela a conduit à une amélioration supplémentaire de la limite supérieure des oméga, la réduisant à 2.371552. Les auteurs ont également généralisé cette même technique pour améliorer le processus de multiplication des rectangles (nParm) matrices - une procédure qui a des applications dans la théorie des graphes, l'apprentissage automatique et d'autres domaines.

De nouveaux progrès dans ce sens sont presque certains, mais il y a des limites. En 2015, Le Gall et deux collaborateurs prouvé que l’approche actuelle – la méthode laser couplée à la recette Coppersmith-Winograd – ne peut pas produire un oméga inférieur à 2.3078. Pour apporter d'autres améliorations, a déclaré Le Gall, « vous devez améliorer l'[approche] originale de Coppersmith et Winograd qui n'a pas vraiment changé depuis 1987.. » Mais jusqu’à présent, personne n’a trouvé de meilleure solution. Il se peut même qu’il n’y en ait pas.

"Améliorer les oméga fait en fait partie de la compréhension de ce problème", a déclaré Zhou. « Si nous pouvons bien comprendre le problème, nous pourrons alors concevoir de meilleurs algorithmes pour le résoudre. [Et] les gens en sont encore aux tout premiers stades de la compréhension de ce problème séculaire. »