Introduction
Dans cet article, nous explorerons ce qu'est tests d'hypothèses, en nous concentrant sur la formulation d'hypothèses nulles et alternatives, la mise en place de tests d'hypothèses et nous plongerons en profondeur dans les tests paramétriques et non paramétriques, en discutant de leurs hypothèses respectives et de leur implémentation en python. Mais nous nous concentrerons principalement sur les tests non paramétriques comme le test U de Mann-Whitney et le test de Kruskal-Wallis. À la fin, vous aurez une compréhension complète des tests d'hypothèses et des outils pratiques pour appliquer ces concepts dans vos propres analyses statistiques.
Objectifs d'apprentissage
- Comprendre les principes du test d'hypothèses, y compris la formulation d'hypothèses nulles et alternatives.
- Mise en place du test d'hypothèse.
- Compréhension du test paramétrique et de ses types.
- Compréhension du test non paramétrique et de ses types ainsi que de ses implémentations.
- Différence entre paramétrique et non paramétrique.
Table des matières
Qu’est-ce que le test d’hypothèse ?
L'hypothèse est une affirmation formulée par une personne/une organisation. L'allégation porte généralement sur des paramètres de population tels que la moyenne ou la proportion et nous recherchons des preuves à partir d'un échantillon pour étayer l'allégation.
Les tests d'hypothèse, parfois appelés tests de signification, sont une méthode permettant de confirmer une affirmation ou une hypothèse concernant un paramètre dans une population à l'aide de données mesurées dans un échantillon. À l'aide de cette méthode, nous explorons plusieurs théories en déterminant la possibilité que, si l'hypothèse des paramètres de population s'était avérée vraie, un échantillon statistique aurait pu être sélectionné.
Les tests d’hypothèses impliquent la formulation de deux hypothèses :
- Hypothèse nulle (H0)
- Hypothèse alternative (H1)
Hypothèse nulle : Il s’agit généralement d’une hypothèse d’absence de différence et généralement notée H0. Selon RA Fisher, l'hypothèse nulle est l'hypothèse dont le rejet éventuel est testé en supposant qu'elle est vraie (Ref Fundamentals of Mathematical Statistics).
Hypothèse alternative: Toute hypothèse complémentaire à l’hypothèse nulle est appelée hypothèse alternative, généralement notée H1.
L'objectif du test d'hypothèse est de rejeter ou de conserver une hypothèse nulle afin d'établir une relation statistiquement significative entre deux variables (généralement une variable indépendante et une variable dépendante, c'est-à-dire généralement l'une est la cause et l'autre l'effet).
Configuration du test d'hypothèse
- Décrivez l’hypothèse avec des mots ou faites une affirmation.
- Sur la base de la revendication, définissez des hypothèses nulles et alternatives.
- Identifiez le type de test d’hypothèse approprié pour l’affirmation ci-dessus.
- Identifiez les statistiques de test à utiliser pour tester la validité de l’hypothèse nulle.
- Décidez des critères de rejet et de rétention de l’hypothèse nulle. C'est ce qu'on appelle la valeur de signification traditionnellement désignée par le symbole α (alpha).
- Calculez la valeur p qui est la probabilité conditionnelle d'observer la valeur statistique du test lorsque l'hypothèse nulle est vraie. En termes simples, la valeur p est la preuve à l’appui de l’hypothèse nulle.
Test paramétrique et non paramétrique
Les tests statistiques non paramétriques ne reposent pas sur des hypothèses concernant les paramètres des distributions de population à partir desquelles les données sont échantillonnées, contrairement aux tests statistiques paramétriques.
Tests paramétriques
La plupart des tests statistiques sont effectués sur la base d’un ensemble d’hypothèses. L'analyse peut donner lieu à des conclusions trompeuses ou complètement fausses lorsque certaines hypothèses ne sont pas respectées.
Généralement, les hypothèses sont les suivantes :
- Normalité : La distribution d'échantillonnage des paramètres à tester suit une distribution normale (ou au moins symétrique).
- Homogénéité des variances : la variance des données est la même entre les différents groupes, sauf si nous testons les moyennes de population provenant de deux populations différentes.
Certains des tests paramétriques sont :
- Test Z : Testez la moyenne, la variance ou la proportion de la population lorsque l’écart type de la population est connu.
- Test t de Student : Testez la moyenne, la variance ou la proportion de la population lorsque l’écart type de la population n’est pas connu.
- Test t apparié : Utilisé pour comparer les moyennes de deux groupes ou conditions liés.
- Analyse de variance (ANOVA) : Utilisé pour comparer les moyennes de trois groupes indépendants ou plus.
- Analyse de régression: Utilisé pour évaluer la relation entre une ou plusieurs variables indépendantes et une variable dépendante.
- Analyse de covariance (ANCOVA) : Étend l'ANOVA en incorporant des covariables supplémentaires dans l'analyse.
- Analyse multivariée de variance (MANOVA) : Étend l'ANOVA pour évaluer les différences entre plusieurs variables dépendantes entre les groupes.
Examinons maintenant en profondeur le test non paramétrique.
Test non paramétrique
Pour la première fois, Wolfowitz a utilisé le terme « non paramétrique » en 1942. Pour comprendre l'idée de statistiques non paramétriques, il faut d'abord avoir une compréhension de base des statistiques paramétriques, dont nous venons de discuter. UN test paramétrique nécessite un échantillon qui suit une distribution spécifique (généralement normale). De plus, les tests non paramétriques sont indépendants des hypothèses paramétriques comme la normalité.
Tests non paramétriques (également appelés tests sans distribution car ils ne comportent pas d'hypothèses sur la distribution de la population). Les tests non paramétriques impliquent que les tests ne sont pas basés sur l'hypothèse que les données sont tirées d'un distribution de probabilité défini par des paramètres tels que la moyenne, la proportion et l’écart type.
Les tests non paramétriques sont utilisés lorsque :
- Le test ne porte pas sur le paramètre de population tel que la moyenne ou la proportion.
- La méthode ne nécessite pas d'hypothèses sur la répartition de la population (par exemple, la population suit une distribution normale).
Types de tests non paramétriques
Discutons maintenant du concept et de la procédure à suivre pour effectuer le test du Chi carré, le test de Mann-Whitney, le test de Wilcoxon Signed Rank et les tests de Kruskal-Wallis :
Test du chi carré
Pour déterminer si l’association entre deux variables qualitatives est statistiquement significative, il faut effectuer un test de signification appelé test du Chi carré.
Il existe deux principaux types de tests du Chi carré :
Qualité de l'ajustement du chi carré
Utilisez le test d'adéquation pour décider si une population avec une distribution inconnue « correspond » à une distribution connue. Dans ce cas, il y aura une seule question d’enquête qualitative ou un seul résultat d’une expérience portant sur une seule population. La qualité de l'ajustement est généralement utilisée pour déterminer si la population est uniforme (tous les résultats se produisent avec la même fréquence), si la population est normale ou si la population est la même qu'une autre population avec une distribution connue. Les hypothèses nulles et alternatives sont :
- H0: La population correspond à la distribution donnée.
- Ha: La population ne correspond pas à la répartition donnée.
Comprenons cela avec un exemple
| Jour | lundi XNUMX | Mardi | Mercredi | Jeudi | Vendredi | Samedi | Dimanche |
| Nombre de pannes | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
Le tableau montre le nombre de pannes dans un facteur. Dans cet exemple, une seule variable est présente et nous devons déterminer si la distribution observée (donnée dans le tableau) correspond ou non à la distribution attendue.
Pour cela, l’hypothèse nulle et l’hypothèse alternative seront formulées comme suit :
- H0:Les pannes sont uniformément réparties.
- Ha: Les répartitions ne sont pas uniformément réparties.
Et le degré de liberté sera n-1 (dans ce cas n=7, donc df = 7-1=6)
Expected value will be= (14+22+16+18+12+19+11)/7=16
| Jour | lundi XNUMX | Mardi | Mercredi | Jeudi | Vendredi | Samedi | Dimanche |
| Nombre de pannes (constatées) | 14 | 22 | 16 | 18 | 12 | 19 | 11 |
| attendu | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| (observé-attendu) | -2 | 6 | 0 | 2 | -4 | 3 | -5 |
| (observé-attendu) ^ 2 | 4 | 36 | 0 | 4 | 16 | 9 | 25 |
En utilisant cette formule Calculer le Chi carré
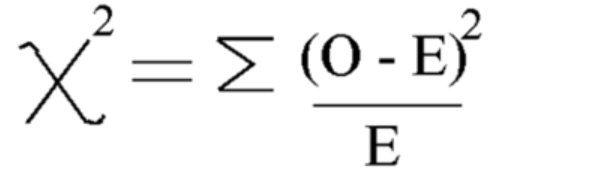
Chi carré = 5.875
Et le degré de liberté est = n-1=7-1=6
Voyons maintenant la valeur critique de tableau de distribution du chi carré au niveau de signification de 5 %
La valeur critique est donc 12.592
Puisque la valeur calculée du Chi carré est inférieure à la valeur critique, nous acceptons l'hypothèse nulle et pouvons conclure que les pannes sont uniformément distribuées.
Indépendance du chi carré du test
Utilisez le test d'indépendance pour décider si deux variables (facteurs) sont indépendantes ou dépendantes, c'est-à-dire si ces deux variables ont ou non une relation d'association significative entre elles. Dans ce cas, il y aura deux questions d'enquête ou expériences qualitatives et un tableau de contingence sera construit. Le but est de voir si les deux variables ne sont pas liées (indépendantes) ou liées (dépendantes). Les hypothèses nulles et alternatives sont :
- H0: Les deux variables (facteurs) sont indépendantes.
- Ha: Les deux variables (facteurs) sont dépendantes.
Prenons un exemple
Exemple dans lequel nous voulons vérifier si le sexe et la couleur préférée de la chemise étaient indépendants. Cela signifie que nous voulons savoir si le sexe d'une personne influence son choix de couleur. Nous avons mené une enquête et organisé les données dans le tableau.
Ce tableau contient les valeurs observées :
| Noir | Blanc | Rouge | Bleu | |
| Homme | 48 | 12 | 33 | 57 |
| Femme | 34 | 46 | 42 | 26 |
Maintenant, formulez d’abord des hypothèses nulles et alternatives
- H0: Le sexe et la couleur de chemise préférée sont indépendants
- Ha: Le sexe et la couleur de chemise préférée ne sont pas indépendants
Pour calculer les statistiques du test du chi carré, nous devons calculer la valeur attendue. Alors, additionnez toutes les lignes et colonnes et les totaux globaux :
| Noir | Blanc | Rouge | Bleu | Total | |
| Homme | 48 | 12 | 33 | 57 | 150 |
| Femme | 34 | 46 | 42 | 26 | 148 |
| Total | 82 | 58 | 75 | 83 | 298 |
Après cela, nous pouvons calculer le tableau des valeurs attendues à partir du tableau ci-dessus pour chaque entrée en utilisant cette formule = (total de la ligne * total de la colonne)/total global
Tableau des valeurs attendues :
| Noir | Blanc | Rouge | Bleu | |
| Homme | 41.3 | 29.2 | 37.8 | 41.8 |
| Femme | 40.7 | 28.8 | 37.2 | 41.2 |
Calculez maintenant la valeur du chi carré en utilisant la formule du test du chi carré :
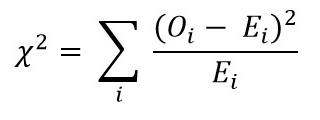
- Oi = Valeur observée
- Ei = valeur attendue
La valeur que nous obtenons est : Χ2 = 34.9572
Calculer le degré de liberté
DF=(nombre de ligne-1)*(nombre de colonne-1)
Maintenant, trouvez et comparez la valeur critique au test du chi carré valeur statistique :
Pour ce faire, vous pouvez rechercher le degré de liberté et le niveau de signification (alpha) à partir du tableau de distribution du chi carré
À alpha =0.050, nous obtiendrons valeur critique= 7.815
Depuis chi carré > valeur critique
Par conséquent, nous rejetons l’hypothèse nulle et pouvons conclure que le sexe et la couleur de chemise préférée ne sont pas indépendants.
Implémentation du Chi Carré
Voyons maintenant l'implémentation du Chi-Carré en utilisant un exemple réel en python :
- H0: Le sexe et la couleur de chemise préférée sont indépendants
- Ha: Le sexe et la couleur de chemise préférée ne sont pas indépendants
Création d'un ensemble de données :
import pandas as pd
from scipy.stats import chi2_contingency
from scipy.stats import chi2
# Given dataset
df_dict = {
'Black': [48, 34],
'White': [12, 46],
'Red': [33, 42],
'Blue': [57, 26]
}
dataset_table = pd.DataFrame(df_dict, index=['Male', 'Female'])
print("Dataset Table:")
print(dataset_table)
print()
# Observed Values
Observed_Values = dataset_table.values
print("Observed Values:")
print(Observed_Values)
print()
# Perform chi-square test
val = chi2_contingency(dataset_table)
Expected_Values = val[3]
print("Expected Values:")
print(Expected_Values)
print()
# Degree of Freedom
no_of_rows = len(dataset_table.iloc[0:2, 0])
no_of_columns = 4
ddof = (no_of_rows - 1) * (no_of_columns - 1)
print("Degree of Freedom:", ddof)
print()
# Chi-square statistic
chi_square = sum([(o - e) ** 2. / e for o, e in zip(Observed_Values, Expected_Values)])
chi_square_statistic = chi_square[0] + chi_square[1]
print("Chi-square statistic:", chi_square_statistic)
print()
# Critical value
alpha = 0.05
critical_value = chi2.ppf(q=1-alpha, df=ddof)
print('Critical value:', critical_value)
print()
# p-value
p_value = 1 - chi2.cdf(x=chi_square_statistic, df=ddof)
print('p-value:', p_value)
print()
# Significance level
print('Significance level:', alpha)
print('p-value:', p_value)
print('Degree of Freedom:', ddof)
print()
# Hypothesis testing
if chi_square_statistic >= critical_value:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
print()
if p_value <= alpha:
print("Reject H0, Gender and preferred shirt color are independent")
else:
print("Fail to reject H0, Gender and preferred shirt color are not independent")
Sortie :
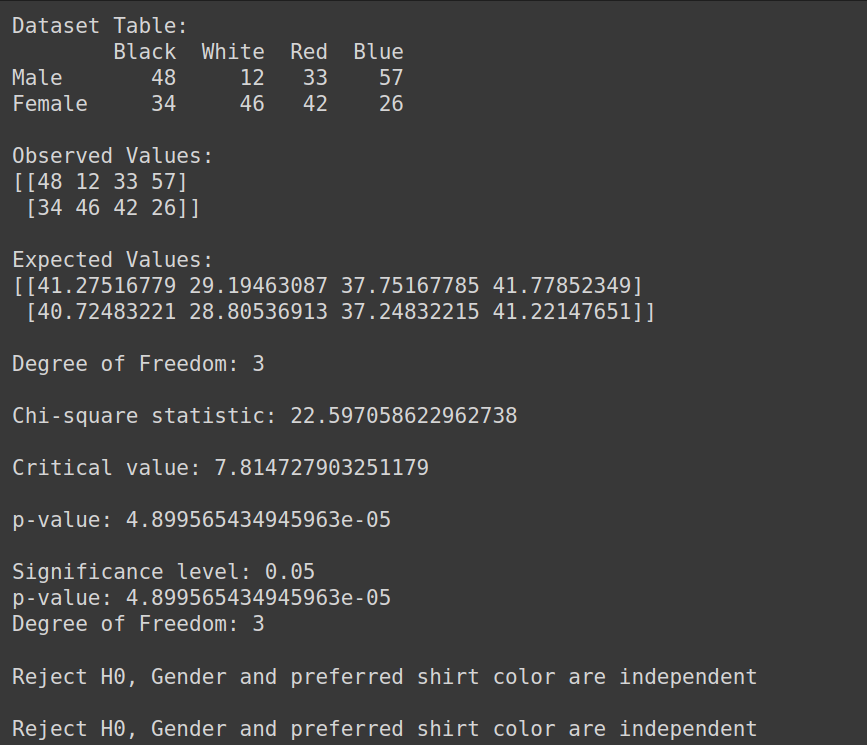
Test Mann-Whitney U
Le test U de Mann-Whitney constitue une alternative non paramétrique au test t pour échantillon indépendant. Il compare deux moyennes d'échantillons de la même population, déterminant si elles sont égales. Ce test est généralement utilisé pour les données ordinales ou lorsque les hypothèses du test t ne sont pas satisfaites.
Le test Mann-Whitney U classe toutes les valeurs des deux groupes ensemble, puis additionne les classements pour chaque groupe. Il calcule la statistique de test, U, sur la base de ces classements. La statistique U est comparée à une valeur critique issue d'un tableau ou calculée à l'aide d'une approximation. Si la statistique U est inférieure à la valeur critique, l’hypothèse nulle est rejetée.
Ceci est différent des tests paramétriques comme le test t, qui comparent les moyennes et supposent une distribution normale. Le test U de Mann-Whitney compare les classements et ne nécessite pas l'hypothèse d'une distribution normale.
Comprendre le test U de Mann-Whitney peut être difficile car les résultats sont présentés sous forme de différences de rang de groupe plutôt que de différences moyennes de groupe.
Formule du test de Mann-Whitney :
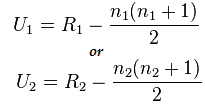
U=min(U1,U2)
Ici,
- U = Test U de Mann-Whitney
- n1 = taille d'échantillon un
- n2 = taille de l'échantillon deux
- R1= Rang de la taille de l'échantillon un
- R2= Rang de la taille de l'échantillon 2
Alors, comprenons cela avec un court exemple :
Supposons que nous souhaitions comparer l'efficacité de deux méthodes de traitement différentes (méthode A et méthode B) pour améliorer la santé des patients. Nous disposons des données suivantes :
- Méthode A : 3,4,2,6,2,5
- Méthode B : 9,7,5,10,6,8
Ici, nous pouvons voir que les données ne sont pas normalement distribuées et que les tailles d’échantillon sont petites.
Implémentation du test U de Mann-Whitney
Maintenant, effectuons le test Mann-Whitney U :
Mais formulons d’abord l’hypothèse nulle et alternative
- H0: Il n'y a pas de différence entre le Rang de chaque traitement
- Ha: Il y a une différence entre le rang de chaque traitement
Combinez tous les soins : 3,4,2,6,2,5,9,7,5,10,6,8
Données triées : 2,2,3,4,5,5,6,6,7,8,9,10
Rang des données triées : 1,2,3,4,5,6,7,8,9,10,11,12
- Classement des données séparément :
- Method A: 3(3),4(4),2(1.5),6(7.5),2(1.5),5(5.5)
- Method B: 9(11),7(9),5(5.5),10(12),6(1.5),8(10)
- Calcul de la somme des rangs) :
- R1: 3+4+1.5+7.5+1.5+5.5=23
- R2: 11+9+5.5+12+1.5+10=55
Calculez maintenant la valeur statistique en utilisant cette formule :
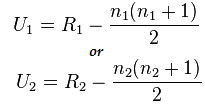
Ici n1=6 et n2=6
Et la valeur après calcul pour U1=2 et pour U2= 34
Calcul de la statistique U :
Nous= min(U1,U2)= min(2,34)= 2
Du Table Mann-Whitney nous pouvons trouver la valeur critique
Dans ce cas, la valeur critique sera de 5
Puisque Uc = 5, ce qui est supérieur à Us au niveau de signification de 5 %. Nous rejetons donc H0
Nous pouvons donc conclure qu’il existe une différence entre le rang de chaque traitement.
Implémentation avec python
from scipy.stats import mannwhitneyu, norm
import numpy as np
TreatmentA = np.array([3,4,2,6,2,5])
TreatmentB = np.array([9,7,5,10,6,8])
# Perform Mann-Whitney U test
U_statistic, p_value = mannwhitneyu(TreatmentA, TreatmentB)
# Print the result
print(f'The U-statistic is {U_statistic:.2f} and the p-value is {p_value:.4f}')
if p_value < 0.05:
print("Reject Null Hypothesis: There is a significant difference between the Rank of each treatment.")
else:
print("Fail to Reject Null Hypothesis: Fail to Reject Null Hypothesis: There is no enough evidence to conclude that there is difference between the Rank of each treatment")Sortie :

Test Kruskal-Wallis
Le test Kruskal-Wallis est utilisé avec plusieurs groupes. Il s'agit d'une alternative non paramétrique et précieuse à un test ANOVA unidirectionnel lorsque les hypothèses de normalité et d'égalité de variance sont violées. Le test Kruskal-Wallis compare les médianes de plus de deux groupes indépendants.
Il teste l'hypothèse nulle lorsque k échantillons indépendants (k>=3) sont tirés d'une population de distributions identiques, sans nécessiter la condition de normalité pour les populations.
Hypothèses:
Assurez-vous qu’il y a au moins trois échantillons aléatoires tirés indépendamment. Chaque échantillon contient au moins 5 observations, n>=5
Prenons un exemple où nous voulons déterminer si la technique d'étude utilisée par trois groupes d'étudiants affecte leurs résultats aux examens. Nous pouvons utiliser le test de Kruskal-Wallis pour analyser les données et évaluer s'il existe des différences statistiquement significatives dans les résultats aux examens entre les groupes.
Formulez l’hypothèse nulle pour cela comme suit :
- H0: Il n'y a aucune différence dans les résultats aux examens entre les trois groupes d'étudiants.
- Ha: Il existe une différence dans les résultats aux examens entre les trois groupes d'étudiants.
Test de rang signé de Wilcoxon
Le test de classement signé de Wilcoxon (également connu sous le nom de test de paires assorties de Wilcoxon) est la version non paramétrique du test t pour échantillon dépendant ou du test t pour échantillon apparié. Le test des signes est l’autre alternative non paramétrique au test t pour échantillons appariés. Il est utilisé lorsque les variables d'intérêt sont de nature dichotomique (telles que Homme et Femme, Oui et Non). Le test de classement signé de Wilcoxon est également une version non paramétrique pour un test t sur un échantillon. Le test de classement signé de Wilcoxon compare les médianes des groupes dans deux situations (échantillons appariés) ou compare la médiane du groupe à la médiane hypothétique (un échantillon).
Comprenons cela avec un exemple, supposons que nous ayons des données sur la consommation quotidienne de cigarettes des fumeurs avant et après leur participation à un programme de 8 semaines et que nous voulions déterminer s'il y a une différence significative dans la consommation quotidienne de cigarettes avant et après le programme, alors nous le ferons utilise ce test
La formulation d’hypothèses pour cela sera
- H0: Il n'y a aucune différence dans la consommation quotidienne de cigarettes avant et après le programme.
- Ha: Il y a une différence dans la consommation quotidienne de cigarettes avant et après le programme
Test de normalité
Parlons maintenant des tests de normalité :
Test de Shapiro Wilk
Le test de Shapiro-Wilk évalue si un échantillon de données donné provient d'une population normalement distribuée. C'est l'un des tests les plus couramment utilisés pour vérifier la normalité. Le test est particulièrement utile lorsqu’il s’agit d’échantillons de taille relativement petite.
Dans le test de Shapiro-Wilk :
- Hypothèse nulle : Les données de l'échantillon proviennent d'une population qui suit une distribution normale.
- Hypothèse alternative : Les données de l'échantillon ne proviennent pas d'une population qui suit une distribution normale.
La statistique de test générée par le test de Shapiro-Wilk mesure l'écart entre les données observées et les données attendues sous l'hypothèse de normalité. Si la valeur p associée à la statistique de test est inférieure à un niveau de signification choisi (par exemple 0.05), nous rejetons l'hypothèse nulle, indiquant que les données ne sont pas normalement distribuées. Si la valeur p est supérieure au seuil de signification, nous ne parvenons pas à rejeter l’hypothèse nulle, ce qui suggère que les données peuvent suivre une distribution normale.
Créons d'abord un ensemble de données pour ces tests, vous pouvez utiliser n'importe quel ensemble de données de votre choix :
import pandas as pd
# Create the dictionary with the provided data
data = {
'population': [6.1101, 5.5277, 8.5186, 7.0032, 5.8598],
'profit': [17.5920, 9.1302, 13.6620, 11.8540, 6.8233]
}
# Create the DataFrame
df = pd.DataFrame(data)
response_var=df['profit']
Here, a sample for running Shapiro -Wilk test on python:
from scipy.stats import shapiro
stat, p_val = shapiro(response_var)
print(f'Shapiro-Wilk Test: Statistic={stat} p-value={p_val}')
if p_val > alpha:
print('Data looks normal (fail to reject H0)')
else:
print('Data looks normal (fail to reject H0)')Sortie :

Ce test est le plus approprié pour des échantillons de taille relativement petite (n = < 50-2000 XNUMX), car il devient moins fiable avec des échantillons de plus grande taille.
Anderson-Darling
Il évalue si un échantillon donné de données provient d'une distribution spécifiée, telle que la distribution normale. Il est similaire au test de Shapiro-Wilk mais est plus sensible, en particulier pour les échantillons de plus petite taille.
Elle convient à plusieurs distributions, y compris la distribution normale, pour les cas où les paramètres de la distribution sont inconnus.
Ici, le code Python pour l'implémenter :
from scipy.stats import anderson
response_var = data['profit']
alpha = 0.05
# Anderson-Darling Test
result = anderson(response_var)
print(f'Anderson statistics: {result.statistic:.3f}')
if result.statistic > result.critical_values[-1]:
p_value = 0.0 # The p-value is essentially 0 if the statistic exceeds the largest critical value
else:
p_value = result.significance_level[result.statistic < result.critical_values][-1]
print("P-value:", p_value)
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")Sortie :

Essai de Jarque-Béra
Le test de Jarque-Bera évalue si un échantillon de données donné provient d'une population normalement distribuée. Il est basé sur l’asymétrie et l’aplatissement des données.
Voici l'implémentation du test Jarque-Bera en Python avec des exemples de données :
from scipy.stats import jarque_bera
# Performing Jarque-Bera test
test_statistic, p_value = jarque_bera(response_var)
print("Jarque-Bera Test Statistic:", test_statistic)
print("P-value:", p_value)
# Interpreting results
alpha = 0.05
if p_value < alpha:
print("Reject null hypothesis: Data does not look normally distributed")
else:
print("Fail to reject null hypothesis: Data looks normally distributed")Sortie :

| Catégories | Techniques statistiques paramétriques | Statistiques non paramétriquesTechniques |
| corrélation | Coefficient de corrélation du moment du produit de Pearson (r) | Corrélation du coefficient de rang de Spearman (Rho), Tau de Kendall |
| Deux groupes, des mesures indépendantes | Test t indépendant | Test U de Mann-Whitney |
| Plus de deux groupes, mesures indépendantes | ANOVA unidirectionnelle | ANOVA unidirectionnelle de Kruskal-Wallis |
| Deux groupes, mesures répétées | Test t apparié | Test de classement signé par paire appariée de Wilcoxon |
| Plus de deux groupes, mesures répétées | ANOVA à mesures répétées et unidirectionnelles | Analyse bidirectionnelle de la variance de Friedman |
Conclusion
Tests d'hypothèses est essentiel pour évaluer les affirmations sur les paramètres de la population à l’aide d’échantillons de données. Les tests paramétriques reposent sur des hypothèses spécifiques et conviennent aux données d'intervalle ou de ratio, tandis que les tests non paramétriques sont plus flexibles et applicables aux données nominales ou ordinales sans hypothèses de distribution strictes. Des tests tels que Shapiro-Wilk et Anderson-Darling évaluent la normalité, tandis que le Chi carré et Jarque-Bera évaluent la qualité de l'ajustement. Comprendre les différences entre les tests paramétriques et non paramétriques est crucial pour sélectionner l’approche statistique appropriée. Dans l’ensemble, les tests d’hypothèses fournissent un cadre systématique pour prendre des décisions fondées sur des données et tirer des conclusions fiables à partir de preuves empiriques.
Prêt à maîtriser l’analyse statistique avancée ? Inscrivez-vous dès aujourd'hui à notre cours d'analyse de données BlackBelt ! Bénéficiez d'une expertise dans les tests d'hypothèses, les tests paramétriques et non paramétriques, l'implémentation de Python, et bien plus encore. Élevez vos compétences statistiques et excellez dans la prise de décision basée sur les données. Adhérer maintenant!
Foire aux Questions
A. Les tests paramétriques font des hypothèses sur la distribution de la population et sur des paramètres tels que la normalité et l'homogénéité de la variance, alors que les tests non paramétriques ne s'appuient pas sur ces hypothèses. Les tests paramétriques ont plus de puissance lorsque les hypothèses sont satisfaites, tandis que les tests non paramétriques sont plus robustes et applicables dans un plus large éventail de situations, notamment lorsque les données sont asymétriques ou ne sont pas normalement distribuées.
A. Le test du chi carré est utilisé pour déterminer s'il existe une association significative entre deux variables catégorielles. Il analyse généralement des données catégorielles et teste des hypothèses sur l'indépendance des variables dans les tableaux de contingence.
A. Le test U de Mann-Whitney compare deux groupes indépendants lorsque la variable dépendante est ordinale ou n'est pas normalement distribuée. Il évalue s'il existe une différence significative entre les médianes des deux groupes.
A. Le test de Shapiro-Wilk évalue si un échantillon provient d'une population normalement distribuée. Il teste l'hypothèse nulle selon laquelle les données suivent une distribution normale. Si la valeur p est inférieure au niveau de signification choisi (par exemple 0.05), nous rejetons l'hypothèse nulle, concluant que les données ne sont pas normalement distribuées.
- Contenu propulsé par le référencement et distribution de relations publiques. Soyez amplifié aujourd'hui.
- PlatoData.Network Ai générative verticale. Autonomisez-vous. Accéder ici.
- PlatoAiStream. Intelligence Web3. Connaissance Amplifiée. Accéder ici.
- PlatonESG. Carbone, Technologie propre, Énergie, Environnement, Solaire, La gestion des déchets. Accéder ici.
- PlatoHealth. Veille biotechnologique et essais cliniques. Accéder ici.
- La source: https://www.analyticsvidhya.com/blog/2024/04/a-comprehensive-guide-on-non-parametric-tests/



