Introduction
Une technique statistique fiable pour déterminer la signification est l’analyse de variance (ANOVA), en particulier lors de la comparaison de plus de deux moyennes d’échantillons. Bien que la distribution t soit adéquate pour comparer les moyennes de deux échantillons, une ANOVA est nécessaire lorsque l'on travaille avec trois échantillons ou plus à la fois afin de déterminer si leurs moyennes sont les mêmes ou non puisqu'ils proviennent de la même population sous-jacente.
Par exemple, l'ANOVA peut être utilisée pour déterminer si différents engrais ont des effets différents sur la production de blé dans différentes parcelles et si ces traitements fournissent des résultats statistiquement différents pour la même population.

Le professeur RA Fisher a introduit le terme « analyse de variance » en 1920 lorsqu'il abordait le problème de l'analyse des données agronomiques. La variabilité est une caractéristique fondamentale des événements naturels. La variation globale dans un ensemble de données donné provient de plusieurs sources, qui peuvent être largement classées comme causes attribuables et aléatoires.
La variation due à des causes attribuables peut être détectée et mesurée tandis que la variation due à des causes fortuites échappe au contrôle de la main humaine et ne peut être traitée séparément.
Selon RA Fisher, l'analyse de variance (ANOVA) est la « séparation de la variance attribuable à un groupe de causes de la variance attribuable à un autre groupe ».
Objectifs d'apprentissage
- Comprendre le concept d'analyse de variance (ANOVA) et son importance dans l'analyse statistique, en particulier lors de la comparaison de moyennes sur plusieurs échantillons.
- Découvrez les hypothèses requises pour réaliser un test ANOVA et son application dans différents domaines tels que la médecine, l'éducation, le marketing, la fabrication, la psychologie et l'agriculture.
- Explorez le processus étape par étape de réalisation d'une ANOVA unidirectionnelle, y compris la définition d'hypothèses nulles et alternatives, la collecte et l'organisation des données, le calcul des statistiques de groupe, la détermination de la somme des carrés, le calcul des degrés de liberté, le calcul des carrés moyens. , calcul des statistiques F, détermination de la valeur critique et prise de décision.
- Obtenez des informations pratiques sur la mise en œuvre d'un test ANOVA unidirectionnel en Python à l'aide de la bibliothèque scipy.stats.
- Comprendre le niveau de signification et l'interprétation de la statistique F et de la valeur p dans le contexte de l'ANOVA.
- Découvrez les méthodes d'analyse post-hoc telles que la différence honnêtement significative (HSD) de Tukey pour une analyse plus approfondie des différences significatives entre les groupes.
Table des matières
Hypothèses pour le TEST ANOVA
Le test ANOVA est basé sur les statistiques du test F.
Les hypothèses formulées concernant la validité du test F dans l'ANOVA sont les suivantes :
- Les observations sont indépendantes.
- La population parentale à partir de laquelle les observations sont prises est normale.
- Divers traitements et effets environnementaux sont de nature additive.
ANOVA unidirectionnelle
Dans un sens, l'ANOVA est un test statistique utilisé pour déterminer s’il existe des différences statistiquement significatives dans les moyennes de trois groupes ou plus pour un seul facteur (variable indépendante). Il compare la variance entre les groupes à la variance au sein des groupes pour évaluer si ces différences sont probablement dues au hasard ou à un effet systématique du facteur.
Plusieurs cas d'utilisation de l'ANOVA unidirectionnelle provenant de différents domaines sont :
- Médicament: L'ANOVA unidirectionnelle peut être utilisée pour comparer l'efficacité de différents traitements sur une condition médicale particulière. Par exemple, cela pourrait être utilisé pour déterminer si trois médicaments différents ont des effets significativement différents sur la réduction de la tension artérielle.
- L'Education: L'ANOVA unidirectionnelle peut être utilisée pour analyser s'il existe des différences significatives dans les résultats des tests entre les étudiants qui ont suivi un enseignement utilisant différentes méthodes d'enseignement.
- Marketing: L'ANOVA unidirectionnelle peut être utilisée pour évaluer s'il existe des différences significatives dans les niveaux de satisfaction des clients entre les produits de différentes marques.
- Fabrication: L'ANOVA unidirectionnelle peut être utilisée pour analyser s'il existe des différences significatives dans la résistance des matériaux produits par différents processus de fabrication.
- Psychologie: L'ANOVA unidirectionnelle peut être utilisée pour déterminer s'il existe des différences significatives dans les niveaux d'anxiété entre les participants exposés à différents facteurs de stress.
- Agriculture: L'ANOVA unidirectionnelle peut être utilisée pour déterminer si différents engrais conduisent à des rendements agricoles significativement différents dans les expériences agricoles.
Comprenons cela en détail avec l'exemple de l'agriculture :
Dans la recherche agricole, l’ANOVA unidirectionnelle peut être utilisée pour évaluer si différents engrais conduisent à des rendements agricoles significativement différents.
Effet des engrais sur la croissance des plantes
Imaginez que vous étudiez l'impact de différents engrais sur la croissance des plantes. Vous appliquez trois types d’engrais (A, B et C) sur des groupes de plantes distincts. Après une période déterminée, vous mesurez la hauteur moyenne des plantes de chaque groupe. Vous pouvez utiliser l'ANOVA unidirectionnelle pour tester s'il existe une différence significative de hauteur moyenne entre les plantes cultivées avec différents engrais.
Étape 1 : hypothèses nulles et alternatives
La première étape consiste à intensifier les hypothèses nulles et alternatives :
- Hypothèse nulle (H0): Les moyennes de tous les groupes sont égales (il n'y a pas de différence significative dans la croissance des plantes en raison du type d'engrais)
- Hypothèse alternative (H1) : Au moins une moyenne de groupe est différente des autres (le type d’engrais a un effet significatif sur la croissance des plantes).
Étape 2 : Collecte et organisation des données
Après une période de croissance définie, mesurez soigneusement la hauteur finale de chaque plante des trois groupes. Organisez maintenant vos données. Chaque colonne représente un type d'engrais (A, B, C) et chaque ligne contient la hauteur d'une plante individuelle au sein de ce groupe.
Étape 3 : Calculer les statistiques du groupe
- Calculez la hauteur finale moyenne des plantes de chaque groupe d’engrais (A, B et C).
- Calculez le nombre total de plantes observées (N) dans tous les groupes.
- Déterminer le nombre total de groupes (K) dans notre cas, k=3(A, B, C)
Étape 4 : Calculer la somme des carrés
Ainsi, la somme totale des carrés, la somme des carrés entre les groupes et la somme des carrés au sein du groupe seront calculées.
Ici, la somme totale des carrés représente la variation totale de la hauteur finale de toutes les plantes.
La somme des carrés entre groupes reflète la variation observée entre les hauteurs moyennes des trois groupes d'engrais. Et la somme des carrés au sein du groupe capture la variation des hauteurs finales au sein de chaque groupe d'engrais.
Étape 5 : Calculer les degrés de liberté
Les degrés de liberté définissent le nombre d'informations indépendantes utilisées pour estimer un paramètre de population.
- Degrés de liberté entre groupes : k-1 (nombre de groupes moins 1) Donc ici ce sera 3-1 =2
- Degrés de liberté au sein du groupe : Nk (Nombre total d'observations moins nombre de groupes)
Étape 6 : Calculer les carrés moyens
Les carrés moyens sont obtenus en divisant la somme des carrés respective par degrés de liberté.
- Carré moyen entre : Entre-groupes Somme des carrés/degrés de liberté entre-groupes
- Carré moyen intérieur : Somme intra-groupe des carrés/degrés de liberté au sein du groupe
Étape 7 : Calculer les statistiques F
La statistique F est une statistique de test utilisée pour comparer la variation entre les groupes à la variation au sein des groupes. Une statistique F plus élevée suggère un effet potentiellement plus fort du type d’engrais sur la croissance des plantes.
La statistique F pour Anova unidirectionnelle est calculée à l'aide de cette formule :
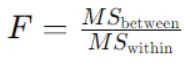
Ici,
MSbetween est le carré moyen entre les groupes, calculé comme la somme des carrés entre les groupes divisée par les degrés de liberté entre les groupes.
MSwithin est le carré moyen au sein des groupes, calculé comme la somme des carrés au sein des groupes divisée par les degrés de liberté au sein des groupes.
- Degrés de liberté entre les groupes (dof_between) : dof_between = k-1
Où k est le nombre de groupes (niveaux) de la variable indépendante.
- Degrés de liberté au sein des groupes (dof_within) : dof_within = Nk
Où N est le nombre d'observations et k est le nombre de groupes (niveaux) de la variable indépendante.
Pour l'ANOVA unidirectionnelle, les degrés de liberté totaux sont la somme des degrés de liberté entre les groupes et au sein des groupes :
dof_total=dof_between+dof_within
Étape 8 : Déterminer la valeur critique et la décision
Choisissez un niveau de signification (alpha) pour l'analyse, généralement 0.05 est choisi
Recherchez la valeur F critique au niveau alpha choisi et les degrés de liberté calculés entre les groupes et les degrés de liberté au sein du groupe à l’aide d’un tableau de distribution F.
Comparez la statistique F calculée avec la valeur F critique
- Si la statistique F calculée est supérieure à la valeur F critique, rejetez l'hypothèse nulle (H0). Cela indique une différence statistiquement significative dans la hauteur moyenne des plantes entre les trois groupes d'engrais.
- Si la statistique F calculée est inférieure ou égale à la valeur F critique, ne parvenez pas à rejeter l'hypothèse nulle (H0). Vous ne pouvez pas conclure à une différence significative sur la base de ces données.
Étape 9 : Analyse post-hoc (si nécessaire)
Si la hypothèse nulle est rejeté, ce qui signifie une différence globale significative, vous voudrez peut-être approfondir. Des mesures post-hoc comme la différence honnêtement significative (HSD) de Tukey peuvent aider à identifier quels groupes d'engrais spécifiques ont des hauteurs moyennes de plantes statistiquement différentes.
Implémentation en Python :
import scipy.stats as stats
# Sample plant height data for each fertilizer type
plant_heights_A = [25, 28, 23, 27, 26]
plant_heights_B = [20, 22, 19, 21, 24]
plant_heights_C = [18, 20, 17, 19, 21]
# Perform one-way ANOVA
f_value, p_value = stats.f_oneway(plant_heights_A, plant_heights_B, plant_heights_C)
# Interpretation
print("F-statistic:", f_value)
print("p-value:", p_value)
# Significance level (alpha) - typically set at 0.05
alpha = 0.05
if p_value < alpha:
print("Reject H0: There is a significant difference in plant growth between the fertilizer groups.")
else:
print("Fail to reject H0: We cannot conclude a significant difference based on this sample.")
Sortie :

Le degré de liberté entre les deux est K-1 = 3-1 =2 , où k représente le nombre de groupes d'engrais. Le degré de liberté à l'intérieur est Nk = 15-3= 12, où N représente le nombre total de points de données.
F-Critique à ddl (2,12) peut être calculé à partir de Tableau de distribution F au niveau de signification de 0.05.
F-Critique = 9.42
Puisque F-Critique < F-statistiques, nous rejetons donc l'hypothèse nulle qui conclut à l'existence d'une différence significative dans la croissance des plantes entre les groupes d'engrais.
Avec une valeur p inférieure à 0.05, notre conclusion reste cohérente : nous rejetons l'hypothèse nulle, indiquant une différence significative dans la croissance des plantes entre les groupes d'engrais.
ANOVA bidirectionnelle
L'ANOVA unidirectionnelle ne convient que pour un seul facteur, mais que se passe-t-il si deux facteurs influencent votre expérience ? Ensuite, l'ANOVA bidirectionnelle est utilisée, ce qui vous permet d'analyser les effets de deux variables indépendantes sur une seule variable dépendante.
Étape 1 : Définir des hypothèses
- Hypothèse nulle (H0): Il n'y a pas de différence significative dans la hauteur finale moyenne des plantes en raison du type d'engrais (A, B, C) ou du moment de plantation (tôt, tard) ou de leur interaction.
- Hypothèse alternative (H1) : Au moins une des affirmations suivantes est vraie :
- Le type d’engrais a un effet significatif sur la hauteur finale moyenne.
- La période de plantation a un effet significatif sur la hauteur finale moyenne.
- Il existe un effet d’interaction significatif entre le type d’engrais et la période de plantation. Cela signifie que l’effet d’un facteur (engrais) dépend du niveau de l’autre facteur (période de plantation).
Étape 2 : Collecte et organisation des données
- Mesurez la hauteur finale des plantes.
- Organisez vos données dans un tableau avec des lignes représentant des usines individuelles et des colonnes pour :
- Type d'engrais (A, B, C)
- Période de plantation (tôt, tard)
- Hauteur finale (cm)
Voici le tableau :

Étape 3 : Calculer la somme des carrés
Semblable à l’ANOVA unidirectionnelle, vous devrez calculer différentes sommes de carrés pour évaluer la variation des hauteurs finales :
- Somme totale des carrés (SST) : Représente la variation totale entre toutes les plantes. Somme des carrés de l’effet principal :
- Types d'engrais intermédiaires (SSB_F) : Reflète la variation due aux différences dans le type d'engrais (moyenne sur les périodes de plantation)
- Temps entre les placages (SSB_T) : Reflète la variation due aux différences dans les périodes de plantation (moyenne selon les types d’engrais).
- Somme des carrés d'interaction (SSI) : Capture la variation due à l’interaction entre le type d’engrais et la période de plantation.
- Somme des carrés au sein du groupe (SSW) : Représente la variation des hauteurs finales au sein de chaque combinaison engrais-temps de plantation.
Étape 4 : Calculer les degrés de liberté (df) :
Les degrés de liberté définissent le nombre d'informations indépendantes pour chaque effet.
- dfTotal : N-1 (observations totales moins 1)
- dfEngrais : Nombre de types d'engrais -1
- dfTemps de plantation : Nombre de fois de plantation -1
- dfInteraction : (Nombre de types d'engrais -1) * (Nombre de périodes de plantation -1)
- dfDans : dfTotal-dfFertilizer-dfplanting-dfInteraction
Étape 5 : Calculer les carrés moyens
Divisez chaque somme de carrés par son degré de liberté correspondant.
- MS_Engrais : SSB_F/dfEngrais
- MS_PlantingTime : SSB_T/dfPlantation
- MS_Interaction : Interaction SSI/df
- MS_Dans : SSW/dfDans
Étape 6 : Calculer les statistiques F
Calculez des statistiques F distinctes pour le type d'engrais, la période de plantation et l'effet d'interaction :
- F_Fertiliser : MS_Fertilizer/MS_Within
- F_PlantingTime : MS_PlantingTime/ MS_Within
- F_Interaction : MS_Inteaction/MS_Within
- F_PlantingTime : MS_PlantingTime/MS_Within
- F_Interaction : MS_Interaction/ MS_Dans
Étape 7 : Déterminer les valeurs critiques et la décision :
Choisissez un niveau de signification (alpha) pour votre analyse, nous prenons généralement 0.05
Recherchez les valeurs F critiques pour chaque effet (engrais, temps de plantation, interaction) au niveau alpha choisi et leurs degrés de liberté respectifs à l’aide d’un tableau de distribution F ou d’un logiciel statistique.
Comparez vos statistiques F calculées aux valeurs F critiques pour chaque effet :
- Si la statistique F est supérieure à la valeur F critique, rejetez l'hypothèse nulle (H0) pour cet effet. Cela indique une différence statistiquement significative.
- Si la statistique F est inférieure ou égale à la valeur F critique, ne rejetez pas H0 pour cet effet. Cela indique une différence statistiquement insignifiante.
Étape 8 : Analyse post-hoc (si nécessaire)
Si l’hypothèse nulle est rejetée, ce qui signifie une différence globale significative, vous souhaiterez peut-être approfondir. Des mesures post-hoc comme la différence honnêtement significative (HSD) de Tukey peuvent aider à identifier quels groupes d'engrais spécifiques ont des hauteurs moyennes de plantes statistiquement différentes.
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols
# Create a DataFrame from the dictionary
plant_heights = {
'Treatment': ['A', 'A', 'A', 'A', 'A', 'A',
'B', 'B', 'B', 'B', 'B', 'B',
'C', 'C', 'C', 'C', 'C', 'C'],
'Time': ['Early', 'Early', 'Early', 'Late', 'Late', 'Late',
'Early', 'Early', 'Early', 'Late', 'Late', 'Late',
'Early', 'Early', 'Early', 'Late', 'Late', 'Late'],
'Height': [25, 28, 23, 27, 26, 24,
20, 22, 19, 21, 24, 22,
18, 20, 17, 19, 21, 20]
}
df = pd.DataFrame(plant_heights)
# Fit the ANOVA model
model = ols('Height ~ C(Treatment) + C(Time) + C(Treatment):C(Time)', data=df).fit()
# Perform ANOVA
anova_table = sm.stats.anova_lm(model, typ=2)
# Print the ANOVA table
print(anova_table)
# Interpret the results
alpha = 0.05 # Significance level
if anova_table['PR(>F)'][0] < alpha:
print("nReject null hypothesis for Treatment factor.")
else:
print("nFail to reject null hypothesis for Treatment factor.")
if anova_table['PR(>F)'][1] < alpha:
print("Reject null hypothesis for Time factor.")
else:
print("Fail to reject null hypothesis for Time factor.")
if anova_table['PR(>F)'][2] < alpha:
print("Reject null hypothesis for Interaction between Treatment and Time.")
else:
print("Fail to reject null hypothesis for Interaction between Treatment and Time.")
Sortie :
Valeur F-critique pour le traitement au degré de liberté (2,12) au niveau de signification de 0.05 à partir de Tableau de distribution F est 9.42
La valeur F-critique pour le temps au degré de liberté (1,12) au niveau de signification de 0.05 est de 61.22.
La valeur critique F pour l'interaction entre le traitement et le temps au niveau de signification de 0.05 au degré de liberté (2,12) est de 9.42.
Puisque F-Critical < F-statistics Nous rejetons donc l’hypothèse nulle pour le facteur de traitement.
Mais pour le facteur temps et l'interaction entre le traitement et le facteur temps, nous n'avons pas réussi à rejeter l'hypothèse nulle car valeur statistique F > valeur F-critique.
Avec une valeur p inférieure à 0.05, notre conclusion reste cohérente : nous rejetons l'hypothèse nulle pour le facteur de traitement tandis qu'avec une valeur p supérieure à 0.05, nous ne parvenons pas à rejeter l'hypothèse nulle pour le facteur temps et l'interaction entre le traitement et le facteur temps.
Différence entre l'ANOVA unidirectionnelle et l'ANOVA à deux facteurs
L'ANOVA unidirectionnelle et l'ANOVA bidirectionnelle sont toutes deux des techniques statistiques utilisées pour analyser les différences entre les groupes, mais elles diffèrent en termes de nombre de variables indépendantes prises en compte et de complexité de la conception expérimentale.
Voici les principales différences entre l’ANOVA unidirectionnelle et l’ANOVA bidirectionnelle :
| Aspect | ANOVA unidirectionnelle | ANOVA bidirectionnelle |
|---|---|---|
| Nombre de variables | Analyse une variable indépendante (facteur) sur une variable dépendante continue | Analyse deux variables indépendantes (facteurs) sur une variable dépendante continue |
| Conception expérimentale | Une variable indépendante catégorielle avec plusieurs niveaux (groupes) | Deux variables indépendantes catégorielles (facteurs), souvent étiquetées A et B, avec plusieurs niveaux. Permet d’examiner les effets principaux et les effets d’interaction |
| Interprétation | Indique des différences significatives entre les moyennes des groupes | Fournit des informations sur les principaux effets des facteurs (A et B) et leur interaction. Aide à évaluer les différences entre les niveaux de facteurs et l'interdépendance |
| Complexité | Relativement simple et facile à interpréter | Plus complexe, analysant les principaux effets de deux facteurs et leur interaction. Nécessite un examen attentif des relations entre les facteurs |
Conclusion
L'ANOVA est un outil puissant pour analyser les différences entre les moyennes des groupes, essentiel lors de la comparaison de plus de deux moyennes d'échantillons. L'ANOVA unidirectionnelle évalue l'impact d'un seul facteur sur un résultat continu, tandis que l'ANOVA bidirectionnelle étend cette analyse pour prendre en compte deux facteurs et leurs effets d'interaction. Comprendre ces différences permet aux chercheurs de choisir l’approche analytique la plus adaptée à leurs conceptions expérimentales et à leurs questions de recherche.
Foire aux Questions
A. ANOVA signifie Analysis of Variance, une méthode statistique utilisée pour analyser les différences entre les moyennes des groupes. Il est utilisé lors de la comparaison des moyennes de trois groupes ou plus afin de déterminer s’il existe des différences significatives.
A. L'ANOVA unidirectionnelle est utilisée lorsque vous disposez d'une variable indépendante catégorielle (facteur) avec plusieurs niveaux et que vous souhaitez comparer les moyennes de ces niveaux. Par exemple, comparer l’efficacité de différents traitements sur un seul résultat.
A. L'ANOVA bidirectionnelle est utilisée lorsque vous disposez de deux variables indépendantes catégorielles (facteurs) et que vous souhaitez analyser leurs effets sur une variable dépendante continue, ainsi que l'interaction entre les deux facteurs. C'est utile pour étudier les effets combinés de deux facteurs sur un résultat.
A. La valeur p dans l'ANOVA indique la probabilité d'observer les données si l'hypothèse nulle (pas de différence significative entre les moyennes des groupes) était vraie. Une valeur p faible (<0.05) suggère qu'il existe des preuves significatives permettant de rejeter l'hypothèse nulle et de conclure à l'existence de différences entre les groupes.)
A. La statistique F dans l'ANOVA mesure le rapport entre la variance entre les groupes et la variance au sein des groupes. Une statistique F plus élevée indique que la variance entre les groupes est plus grande par rapport à la variance au sein des groupes, ce qui suggère une différence significative entre les moyennes des groupes.
- Contenu propulsé par le référencement et distribution de relations publiques. Soyez amplifié aujourd'hui.
- PlatoData.Network Ai générative verticale. Autonomisez-vous. Accéder ici.
- PlatoAiStream. Intelligence Web3. Connaissance Amplifiée. Accéder ici.
- PlatonESG. Carbone, Technologie propre, Énergie, Environnement, Solaire, La gestion des déchets. Accéder ici.
- PlatoHealth. Veille biotechnologique et essais cliniques. Accéder ici.
- La source: https://www.analyticsvidhya.com/blog/2024/04/one-way-and-two-way-analysis-of-variance-anova/



